Differensiallikningar
Når vi løyser ei vanlig likning, så er vi interessert i å finna eit eller fleire tal som passar i likninga. Men når vi løyser ei differensiallikning, så er vi ute etter å finna ein funksjon som passar i likninga. Denne funksjonen kan vi td. kalla y(t), men i likninga set vi ofte bare y.
Eksempel: Vi tenkjer oss ein vanntank med ein kran der det renn ut 30 liter per minutt, og vi lar y(t) stå for vannmengden som funksjon av tida t. Sidan den deriverte y'(t) av funksjonen y er endringen av vannmengde per tid, så kan vi setja opp likninga y' = -30. Minustegnet får vi fordi endringen er negativ. (les meir om dette). Dette er ei enkel differensiallikning som vi kan løysa ved å integrera (antiderivera) begge sider. Vi får då løysinga y(t) = -30t + C. Dette kallar vi for den generelle løysinga, fordi integrasjonskonstanten C, kan vera kva som helst. Men hvis vi veit at tanken ved starten (t = 0) inneheld 1000 liter, så får vi den spesielle løysinga y = -30t + 1000. Dei opplysningane som gjer at vi kan finna den spesielle løysinga, kallast randkrav eller initialbetingelsar.
Ei differensiallikning kan innhalda funksjonen sjøl, den deriverte av funksjonen, den andrederiverte eller av høgare orden, altså y, y', y'' osv. Den kan også innehalda uttrykk med x eller t (den uavhengige variabelen) som vi kan skriva f(x), g(x) osv. Vi skal her ikkje snakka om løysingsmetodar, men sjå litt nærmare på noken typar differensiallikningar og løysingane til disse. Hvis du kan derivasjonsreglane, så kan du kontrollera om dei oppgitte løysingane passar ved å rekna ut y' og evt y'', og setja inn i likninga.
Begrep
La oss først få noken begrep på plass.
Ordinære likningar: Ein ordinær differensiallikning er ein likning
som inneheld den (vanlige) deriverte, ikkje partiell
deriverte. Eksempel på partielle differensiallikningar er Schrödingerlikninga
og Dirac-likninga.
I det følgande konsentrerer vi oss om dei ordinære likningane.
Orden: Vårt første eksempel var av typen y' = K. Dette er
ei førsteordens difflikning fordi det innheld der deriverte y',
men ikkje den andrederiverte y'' eller høgare. Eksempelet
"Harmoniske svingningar" under er av andre orden, sidan det inneheld den
dobbelderiverte y'', men ikkje høgare.
Lineære likningar: Hvis likningen bare inneheld y, y' osv.
av første grad, og ingen y2 , (y')2 eller
høgare grad.
Homogene likningar: Dette kan bety to ting. Enten er det ein likning
der det ikkje fins ledd med bare funksjonar av x, eller det kan bety
likningar på formen
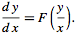
Fleire eksempel:
1: Eksponentiell vekst eller nedgang
Vekst: Eks frå Sinus R2: Vi har ein bakteriekultur som aukar med
20% per døgn. Det betyr at vi kan skriva y' = 0.20*y Den
generelle løysinga er y(t) = C*e0.20*t. Hvis vi antar
at bakteriekulturen i starten hadde 1000 bakterier, dvs at y(0) = 1000,
så betyr det at den spesielle løysinga er y(t) = 1000*e0.20*t.
Dette kallast for eksponentialfunksjonen.
Eksponentiell vekst betyr at ikkje bare er veksten ubegrensa, men den
aukar stadig. Dvs. at grafen blir stadig brattare:
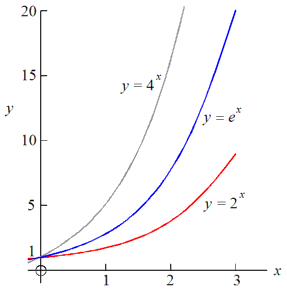
Nedgang: Hvis vi har ein viss mengde av stoffet Thorium-227, så
vil vi etter ca. 19 dagar sitja igjen med halvparten. Resten har omdanna
seg til Radium-223, ved å senda ut ein alfapartikkel. Vi seier at Th-227
har halveringstida 19 dagar. Dette kallar vi for radioaktivt decay eller
henfall / sundfall. Decay er ein tilfeldig prosess. Kvar kjerne har ein
viss sannsynlighet for å falla sund. Det betyr at i gjennomsnitt vil
antallet kjerner som fell sund vera proporsjonale med antalet kjerner.
Dette kan vi oversetja til likninga N'(x) = - l·
N. Dette er den same likninga som for vekst, bare med negativt
fortegn. Generel løysing er C*elt
der konstanten C er lik det antalet vi startar med, dvs. N(0). Sidan
vi her har nedgang, vil grafen flata meir og meir ut:
2: Begrensa vekst: Den logistiske likninga.
Det fins fleire differensiallikningar som prøver å kompensera for den ubegrensa veksten som vi få i forrige eksempel. Ein av dei er den såkalte logistiske likninga:
N' = r N (1 - N/K).
Her er K og r konstantar. K er den bærekraftige kapasiteten, dvs. det maksimale antalet dyr som kan leva i habitatet i ein stabil situasjon, og r er vekstraten som er knytta til fertitliteten. Når N er mykje mindre enn K vil dette koka ned til same situasjon som over, dvs. eksponentiell vekst. Men når N nærmar seg K vil veksten avta fordi faktoren (1 - N/K) vil gå mot null. Denne faktoren har altså med kor mange dyr som dør.
Løysinga er den logistiske funksjonen,: (Med P i staden for N)
Nedanfor er N(t) plotta i grønt. I samme diagrammet er også
eksponentialfunksjonen plotta i rødt.
Fall i tyngdefeltet
Så skal vi sjå på to tilfeller som er ganske like på dei to første, men som likevel har forskjeller.
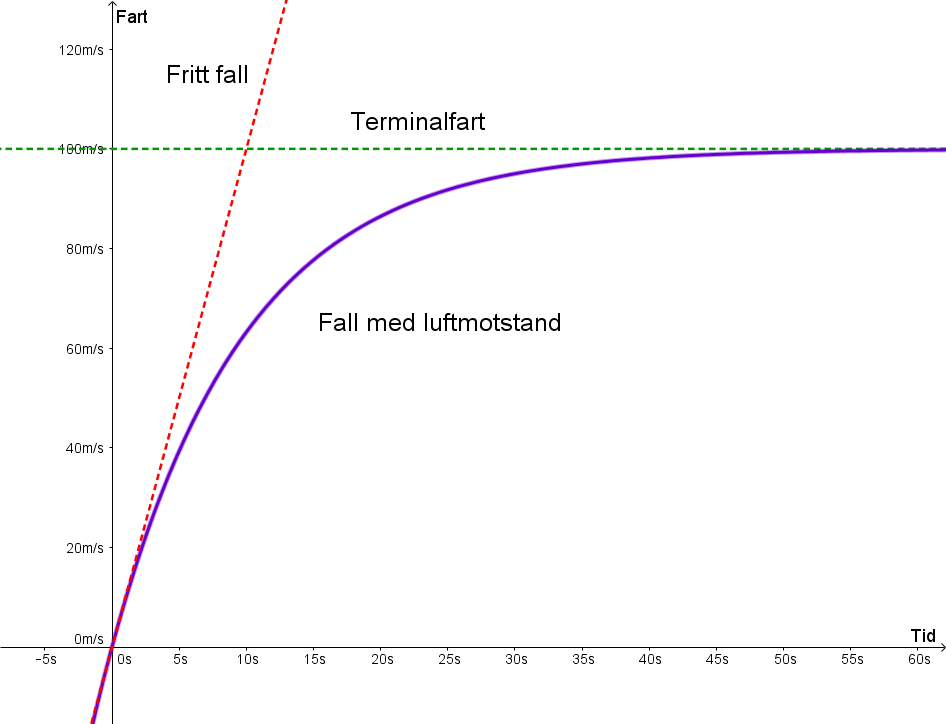
4: Fritt fall (fall uten luftmotstand).
Når bare tyngdekraften virkar så kallar vi det fritt fall. Då gir Newtons andre lov denne likninga: mv' = mg, dvs. v' = g. Dette betyr at akselerasjonen (som er lik v') er lik tyngdeakselerasjonen (9.8 m/s2). Her er det farten v(t) som er vår ukjente funksjon, og dette er matematisk sett identisk til likninga vi starta med, og den generelle løysinga blir v = gt + C. Med initialbetingelsen v(0) = 0, får vi v = gt. Dette er ei rett linje som startar i origo, og har stigningstal lik g.
5: Fall med luftmotstand :
Med luftmostand må vi finna ein modell for kor stor den er. Hvis vi antar at den er proporsjonal med farten, så får vi likninga: mv' = mg - kv. Intuitivt er denne mykje meir realistisk. Konstanten k er avhengig av fasongen og overflata til gjenstanden som fell. Når farten er lav, er luftmostanden liten, og vi har i praksis eit fritt fall. Men etter kvart som farten aukar vil det andre leddet begynna å dominera, og v', dvs. akselerasjonen vil avta. Det vil sei at grafen flatar ut. Når kv er blitt lik mg, betyr det at likninga vår egentlig er v' = 0. Og den har løysing v = konstant. Farten nærmar seg altså ein konstant verdi, som vi kallar terminalfarten. Vi finn at den er lik mg/k.
Den generelle løysinga er v(t) = (mg/k) - Ce(-k/m)t. Med initialbetingelsen v(0) = 0, får vi den spesielle løysinga v(t) = (mg/k)(1 - e(-k/m)t). Vår nye funksjon for v(t) startar ut identisk med tilfellet uten luftmotstand, dvs. som ei rett linje. Men etter kvart vil kurven flata ut og nærma seg terminalfarten.
Les meir om fall i tyngdefeltet: Eit ufritt fall.
Svingningar
6: Udempa svingningar (Harmoniske svingningar) Sjå også eksempel NDLA.
Vi tenkjer oss her eit lodd med masse m som er festa i ei fjør, og som kan gli vannrett fram og tilbake uten motstand. Hvis det ligg på ein svevebane vil friksjonen vera liten, så vi vil sjå bort frå den i første omgang. Oppsettet kan vera slik som dette:
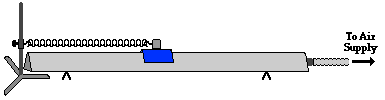
Det er då tre krefter som virkar på loddet: tyngden G, normalkrafta N frå underlaget, og fjørkrafta K. Sidan det ikkje er bevegelse i vertikal retning vil tyngden og normalkraften vera like store, men motsett retta. Så dei opphever kvarandre, og summen av kreftene er derfor lik fjørkrafta. No bruker vi Hookes lov, som seier at krafta vi må bruka for å dra loddet ein avstand x frå likevektspunktet er proporsjonal med x. Krafta frå fjøra på loddet er då: K = -kx. Her er k fjørkonstanten som fortel kor stiv fjøra er, og x er utslaget, dvs. avstanden mellom posisjonen til loddet og likevekstpunktet, der K = 0. Her har vi at x er ein funksjon av tida t, og det er denne vi skal finna. Minustegnet kjem fordi krafta frå fjøra vil virka motsatt av utslaget: den prøver alltid å dra loddet tilbake i likeveksstillinga. Newtons andre lov seier at F = ma, og her får vi då ma = -kx. No er det slik at akselerasjonen a er det same som den deriverte av farten, som igjen er den deriverte av utslaget. Med andre ord er a lik den dobbelderiverte av utslaget: a = x''. Dermed får vi denne differensiallikninga:
mx'' = - kx
Løysinga på denne likninga er på formen:
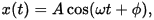
der vi har at
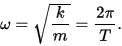
Her er A lik amplituden, dvs. det største utslaget, og T er perioden. Hvis vi drar loddet til sida og slepper det mens det er i ro, så har vi då at A = x(0) og x'(0) = 0. Loddet vil svinga fram og tilbake langs banen i det uendelige, og T er den tida det tar frå vi slepp det til det er tilbake i den posisjonen, altså tida for ein heil svingning. Φ er ein fase, men med våre initialbetingelsar vil den bli 0. Grafen kan dermed sjå slik ut:
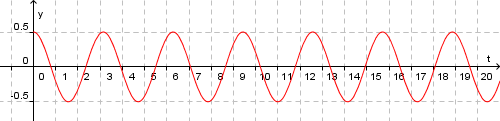
Her er A = 0,5 og T = 3.
7: Dempa svingningar. Sjå også eksempel NDLA.
I eksempelet over er friksjonen og luftmotstanden 0. Slik er det ikkje i verkeligheten. I praksis vil oppsettet vårt over svinga ei stund, men til slutt vil det slå seg til ro. Derfor må vi ha med friksjonen i likninga vår. Hvis vi seier at den er proporsjonal med farten, slik vi hadde i eksempelet med fall, så kan vi altså skriva at friksjonskrafta som −bv. Proporsjonalitetskonstanten b kallast for bremsekonstanten. No får vi ei modifisert differensiallikning:
mx'' = - kx - bx' eller omskriven til mx'' + kx + bx' = 0
Her har vi brukt at v = x'. For å gjera historien kortare kan vi sei at løysinga liknar løysinga vi fekk for udempa svingningar, men med viktige unntak: Vi får ein annan (litt lavare) frekvens, og amplituden vil bli mindre og mindre etter som tida går. Vi kan skriva at A(t) = A0 * e-γt. Her er γ = b/2m. Dette kan fortona seg slik:
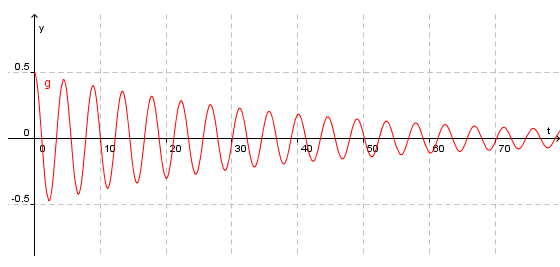
Dersom friksjonen er veldig stor, kan det henda at systemet roar seg ned
før det rekk å svinga ein einaste svingning. I slike tilfeller seier vi at
systemet er overdempa. Interessante ting skjer også med
svingesystem som er påvirka av andre ytre krefter som også svingar med ein
viss frekvens. Men det skal vi ikkje gå inn på her.
Andre eksempel
Det fins massevis av eksempel på anvendelsar av differensiallikningar. Frå fysikken kan vi nevna Maxwell-likningane som gir grunnlaget for den klassiske elektromagnetismen. I biologien har vi også dei såkalte Lotka–Volterra-likningane som prøver å modellera tilfeller der to artar konkurrerer om dei same ressursane, eller der den eine arten lever av den andre. (predator / bytte-forhold). Og så har vi dei kjente Lorenz-likningane som modellerer atmosfærisk konveksjon, og som på mange måtar starta det nye fagfeltet kaos.
Numeriske løysingar
Ofte er det umulig å finna ei løysing ved rekning, dvs det som kallast ei
analytisk løysing. Då må vi gjerne ty til numeriske metodar, dvs tilnærmings
Euler-metoden.
Det fins meir avanserte metodar som gir betre løysingar, slik som Runge-Kutta-metoden.
Til slutt må det nevnast at differensiallikningar, som modellerer
kontinuerlige funksjonar har sin parallell i differens-likningar som
modellerer diskrete størrelsar. Det betyr for eksempel at vi ikkje studerer
funksjonen for alle mulige tider t, men ser heller på funksjonen med jevne
intervall. For eksempel kan vi ved hjelp av Euler-metoden skriva om den
logistiske likninga over til ein differenslikning på følgande form:
Her er xn antalet dyr vi har no, og xn+1 antalet ved tida neste gong. Tida t er erstatta av ein tellevariabel n som tel kor mange tidsintervall som har gått. Denne likninga kallast for den logistiske avbildninga, og du kan leika deg med forskjellige r-verdiar og sjå korleis dette påvirkar tidsutviklinga her.
LENKER
What Is A Differential Equation?Exponential decay.
Harmoniske svingninger.
