Eulermetoden og Eulers tal e
Mange differensiallikningar har ingen eksakte løysingar, og må derfor løysast vha. numeriske metodar på ein datamaskin. Ein slik metode er Eulers metode, oppkalt etter den sveitsiske matematikaren Leonhard Euler. For å sjå korleis denne fungerer, så ser vi på ein veldig enkel differensiallikning der løysinga er kjent, nemlig
y' = y
Løysinga på denne likninga er altså ein funksjon y(t) som er lik sin egen deriverte, nemlig y(t) = et, der e = 2.718281828... er Eulers tal. Dette er eksponentialfunksjonen, og likninga vår medfører uendelig vekst.
For å bruka Eulers metode må vi har eit startpunkt. Så la oss anta at vi i tillegg til likninga over, har initialbetingelsen y(0) = 1. Dette er punktet P0 i figuren under. Sidan y' = y, betyr det at den deriverte i dette punktet også er 1. Dermed kan vi tegna inn tangenten i punktet (stipla linje) som har stigningstal a = 1. Vi veit at når vi går 1 til høgre på x-aksen, så går vi opp på y-aksen ein verdi tilsvarande a. I dette tilfellet havnar vi i punktet P1 = (1,2).
Den grøne kurven på figuren er grafen til løysinga vi er ute etter: et. Vi ser at punktet vi har funne er ein dårlig tilnærming. Men vi kan klara betre. Hvis vi går eit steg som er halvparten så lang til høgre, dvs. set Δt = 0.5, så går vi eit steg a * Δt = 1 * 0.5 = 0.5 opp. Då havnar punktet P1 = (0.5, 1.5). Her kan vi tegna ein ny tangent med stigningstal lik 1.5. Går vi eit nytt steg Δt til høgre, så må vi gå eit steg a * Δt = 1.5 * 0.5 = 0.75 opp. Då havnar vi i punkt p2 = (1, 2.25), sjå figuren under.
Differansen mellom det verkelige y-verdien i punkt 2, og vår tilnærmingsverdi er fremdeles ganske stor, men vi er nærmare enn i første forsøk. Derfor er det naturlig å prøva med endå mindre steglengde. Så vi prøver med Δt = 0.1. Så over, startar vi i P0 og reknar oss vidare punkt for punkt. Kvar gong vi går eit steg Δt til høgre, så går vi y' * Δt opp. Hvis vi kallar y-verdiane i punkta for y0, y1, y2, osv. Då kan vi skriva følgande formel for y-verdien i punkt Pn+1:
yn+1 = yn + y' * Δt
I vårt eksempel, der vi har at y' = y, så blir likningen:
yn+1 = yn + yn * Δt = yn (1+ Δt)
Dette er ein rekursiv formel som lar oss rekna verdiane ein etter
ein. Med startverdien, y0 = 1, og
steglengde Δt = 0.1 forenklar dette seg til y1
= 1* (1.1), og yn = 1* (1.1)n.
Dermed får vi ei tallfølge med
følgande tal 1.0, 1.1, 1.21, 1.33, 1.46, 1.61, 1.77, 1.95, 2.14, 2.36,
2.59 (avrunda). Dette er plotta i figuren under.
Konvergens
No kan vi sjå igjen på våre tilnærmingsverdiar for t = 1 . I første tilnærming fekk vi y1 = 2. I andre tilnærming fekk vi y2 = 2,25. No finn vi at y(1) = y10 = 1.110 = 2.59. Så vi nærmar oss den korrekte verdien e = 2.718281828. Men spørsmålet er: kan vi komma så nær vi vil? Det ser jo slik ut. Med steglengde Δt = 0.01 får vi at y(1) = y100 = 1.01100 = 2,70. Går vi endå lenger og set Δt = 0.00001 får vi at y(1) = y100000 = 1.00001100000 = 2,718268237. No ser vi at feilen er i femte siffer etter komma. For å sjå at grenseverdien er lik e, kan skriva Δt = 1/n, og la n gå mot uendelig. Då får vi akkurat definisjonen av Eulers tal! (Ein av fleire).
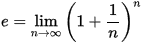
Me andre ord: vi veit at når vi kan komma så nær e vil bare vil, hvis vi lar Δt gå mot null.
Generell formel
La oss samanfatta: For å bruka Eulers metode må differensiallikningen vera på formen
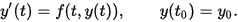
Her er altså den deriverte ein funksjon t og y. Vi finn no ein tilnærmingsverdi for den deriverte: (I likninga under er bokstaven h brukt for steglenden Δt.)
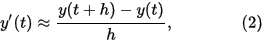
Dermed kan vi finna løysinga med ein iterativ metode der vi finn suksessive y-verdiar vha. formelen
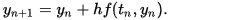
Andre metodar
Eulers metode er den enklaste metoden, men den er ikkje den mest nøyaktige, og den gir ikkje alltid stabile løysingar som konvergerer. Heldigvis fins andre som metodar. Disse kan kategoriserast som Lineære multistep metodar, og Runge-Kutta-metodar. Likevel kan den vera nyttig. I filmen Hidden Figures, benytta Katherine Johnson Eulers metode for å finna ut korleis dei skulle få astronauten John Glenn ned igjen frå sin bane. Her er eit javascipt-eksempel der du kan løysa ulike differensiallikningar vha eulermetoden.
