Kaos

På 1700- og 1800-talet, då den Newtonske mekanikken triumferte ved å forklara korleis planetene bevega seg rundt solsystemet, meinte jamvel teologar at universet var som eit stort urverk som Gud hadde laga. Og fremdeles tenkjer vi på solsystemet som veldig harmonisk og stabilt, der planetene går i veldefinerte elliptiske banar som ikkje endrar seg. Men det er fordi vi har så kort tidsperspektiv. For i det lange løp er faktisk solsystemt kaotisk. Og det har ikkje bare med det faktum at solsystemet blir påvirka utanfrå av innfanga gjenstandar, men at eit system med mange gjenstandar, kan oppføra seg kaotisk heilt på egen hånd! For to gjenstander som sola og jorda, så lar likningane seg løysa analytisk, men der stopper det også. På nittenhundretalet fant matematikaren Henri Poincaré ut at sjøl eit system med bare tre planeter kan oppføra seg kaotisk. Sjå feks denne animasjonen som viser korleis ei planet kan oppføra i eit system med to soler! Dette kallast for mange legeme-problemet, og generelt er det ikkje mulig å finna analytiske løysingar på dette, bare tilnærma. Når solsystemet likevel er veldig stabilt, har det samanheng med at solmassen er så mykje større enn planetmassane.

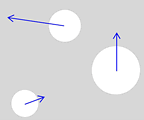
Tre astronomiske objekter som beveger seg i sine respektive gravitasjonsfelt.

Men kva betyr det egentlig at eit system er kaotisk?

1) For det første må systemet vera veldig sensitive til startbetingelsane. Det betyr at ein liten endring kan medføra store endringar på lang sikt. Dette er innhaldet i den ofte siterte (og ofte feilsiterte og feiltolka) sommarfugleffekten. Det var matematikaren og meterologen Edward Lorenz som gav opphav til uttrykket då han oppdaga at dei værsimuleringane han kjørte på  datamaskinen sin, var veldig avhengig av kor mange siffer han brukte for tala som input. Hvis han runda av og skreiv inn 0.506 i staden for 0.506127 så fekk han ikkje bare ulike svar, men veldig ulike svar. Dette har sidan vore populært framstilt i mange ulike variantar, men ein av dei er at hvis ein sommerfugl flaksar med vingene i Brasil, så kan det setta i gang ein tornado i Texas. * (Ein veldig vanlig misforståing er då at det er sommarfuglen som forårsaker tornadoen. Men det er heilheten i startbetingelsane, dvs. summen av alle bevegelsane og alle parameterane som trykk, temperatur, skyer, solinnstråling osv, som foråraker tornadoen. Og sommarfugleffekten betyr då at hvis du endrar ein av disse, td. temperaturen, aldri så lite, så vil systemet utvikla seg på ein heilt annan måte i det lange løp.) Seinare har andre meint at været ikkje er så sensitivt til slike små endringar som dette, men uansett: kaotiske system er ein realitet, sjøl om værsystemet kanskje ikkje er det.

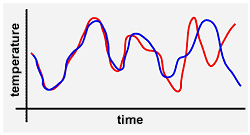
Tidsutviklinga for eit kaotisk system. Grafen viser to ulike forløp med der startbetingelsane er ørlite forskjellige. Sjøl om kurvene er ganske samanfallande i starten, så blir dei meir og meir forskjellige etter kvart.

2) Lorenz presenterte resultata sine med ein graf som viser det fysikarane kallar faserommet til systemet. I dette generaliserte rommet korresponderer kvar av aksane til ein av variablane i systemet. Dynamikken i eit system kan vi visa i eit fasediagram som viser alle mulige tilstandar som systemet kan ha. Som eksempel kan vi sjå på ein eindimensjonal pendel. Variablane er posisjonen x (utslaget) og bevegelsesmengden p (m*v). Vi kan tenkja oss andre, som farten eller den kinetiske eller den potensielle energien, men disse kan vi rekna ut vha x og p. Dersom vi tenkjer oss denne pendelen uten friksjon, så vil bevegelsen fortsetja i det uendelige uten stopp. Faserommet til ein slik idealisert pendel er ein ellipse. For ein verkeleg pendel med friksjon, vil fasediagrammet sjå ut som på figuren under. Etter kvart som tida går blir både det maksimale utslaget (dvs. amplituden) og den maksimale bevegelsesmengda mindre og mindre heilt til pendelen stoppar opp. Fasediagrammet ser derfor ut som ein spiral som endar i sentrum der x = 0, og p = 0. Hvis derimot pendelen er påvirka av ei periodisk kraft som er forskjellig frå egenfrekvensen til pendelen, så får vi ein kaotisk pendel med heilt andre kurver i faserommet.

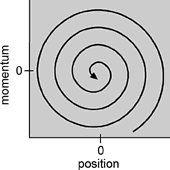
Fasediagramet for ein pendel med friksjon.

Men det fasediagrammet som Lorenz tegna til sine værsimuleringar var heilt ulikt dette. Hans figur likna på eit åttetal der kurven slynger seg rundt to punkt. Men det interessante er at kurven aldri krysser seg sjøl. Det betyr at systemet aldri er på nøyaktig same punkt i faserommet. Denne kurven fekk navnet “strange attractor,” og vart eit symbol for det nye feltet kaosforsking. Sjå javascripteksempel.

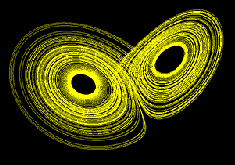
Lorenz-attractoren, som viser ein orden i kaoset.

Populasjonsdynamikk

Kaos viser seg på ei rekke ulike felt som økonomi, elektriske kretsar og elektriske signal i hjertet, i hjernen og, i kunstige nevrale nett, og ikkje minst i økologi. Vi skal her sjå litt nærmare på det siste. Ein nøkkelparameter når ein beskriv dynamikken til ein dyrepopulasjon er vekstraten, som har samanheng med dyrets fertilitet. Hvis vekstraten er høg, kan det oppstå ein situasjon der populasjonen svingar mellom ein høg og ein lav verdi, og altså ikkje har noke likevektspunkt. Ein slik tilsynelatande usannsynlig oppførsel er faktisk observert.  Sjå figuren under.

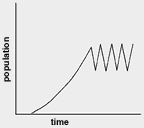
Tidsutviklinga til ein dyrepopulasjon som svingar mellom to verdiar.

På 70-talet studerte biologen Robert May, ein modell for dette basert på denne enkle kvadratiske likninga (også kalla den logistiske avvildningen):

x_n+1 = r*x_n * (1 – x_n)

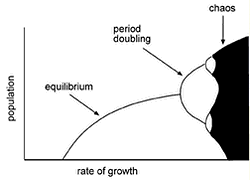
Likningen viser korleis ein kan rekna ut populasjonen i den (n+1)-te generasjonen x_n+1, basert på x_n som er populasjonen i den n-te generasjonen, (skalert slik at 1 er maksimale populasjonen). May undersøkte effekten av vekstraten r. Det viste seg at for lave verdiar, så stabiliserte populasjonen seg på ein verdi. Dette svarar til første del av diagrammet under. Når han auka r, oppdaga han at kurven plutselig delte seg slik at populasjonen har to mulige verdiar. Dette korresponderer med tilfellet over. Når han auka r ytterligare, så deler kurven seg igjen. Slik held det på inntil systemet begynner å oppføra seg kaotisk. Du kan leika deg med forskjellige r-verdiar og sjå korleis dette påvirkar tidsutviklingen her. Eit plott som viser antal løysingar som funksjon av r kallast eit bifurkasjonsplot. Den klassiske periodedoblinga er eit sikkert tegn på kaos. Sjå javascripeksempel.