Eit ufritt fall
Ka skjer når vi slepp ein gjenstand, feks ein fallskjermhoppar, frå stor høyde?
Fritt fall
Galileo Galilei viste at hvis vi slepp ein liten ball og ei tung blykule samtidig, så vil dei også treffa bakken samtidig. Dette er riktig med eit lite, men viktig forbehold: at det er fall uten luftmotstand. For dette handlar om det vi i fysikken kallar fritt fall. Fritt fall er definert som fall der bare tyngdekrafta virkar. Tyngdekrafta til ein gjenstand er gitt ved G = mg, der m er massen, og g er lik tyngdeakselerasjonen, som ved havnivå er ca. 9.8 m/s2. Ein annan måte å definera fritt fall er derfor at gjenstanden fell med ein konstant akselerasjon lik tyngdeakselerasjonen.
Bevegelseslikningane for konstant akselerasjon.
Fritt fall er altså bevegelse med konstant akselerasjon, og to av formlane som vi kan bruka då er
Veiformelen som gir oss posisjonen s(t) som funksjon av tida, og Fartsformelen som gir oss farten v(t) som funksjon av tida:s(t) = v0t + 1/2 a t2
v(t) = v0 + at.
Her er v0 startfarten, men den kan vi kan vi setja lik null, sidan vi tenkjer oss at farten i vertikale retning er null for fallskjermhopparen vår. (Den horisontale er ikkje det, men vi skal bare rekna på vertikale hastigheter) For å gjera rekningen enkel set vi tyngdeakselerasjonen til g = 10 m/s2. Formlane våre blir då:
s(t) = 5t2.
v(t) = 10t.
a(t) = 10
Kurvene til disse tre funksjonane er tegna nedanfor med rødt i kvar sin graf. Posisjonsgrafen for fritt fall er ein andregradsfunksjon (ein parabel), fartsgrafen er ei rett (skrå) linje, og akselerasjonsgrafen er ei horisontal linje. Kva betyr dette i praksis? Det betyr at farten aukar i det uendelige, og det blir feil!
Verkeligheten og Newtons andre lov
For i verkeligheten veit vi at akselerasjonen etter kvart minkar og går mot null. Farten vil då nærma seg ein konstant hastighet som vi kallar for terminalfarten. For ein fallskjermhoppar kan det vera rundt 200 km/h. Men sjøl om den er konstant for ein bestemt hoppar i ein bestemt posisjon, vil den endra seg etter kor stor luftmotstanden er, og kva posisjon hopparen har. Hvis hopparen brettar armar og bein ut blir luftmotstanden stor, og terminalfarten tilsvarande lav. Med hendene inntil kroppen og hode nedover er luftmotstanden betydelig mindre og terminalfarten kan komma opp mot 300 km/h. Også drakta påvirkar luftmotstanden. I speed skydiving kan ein nå hastigheter over 600 km/h.
Nedanfor er ein tegning av kreftene som virkar på ein fallskjermhoppar i fall: Nedover virkar tyngdekrafta G, og oppover virkar luftmotstanden L.
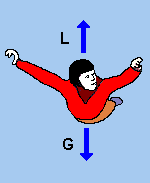
Newtons andre lov seier at summen av kreftene som virkar på ein gjenstand er lik massen til gjenstanden multiplisert med akselerasjonen som den får. Hvis vi reknar positiv retning nedover, så har vi at summen av kreftene er G - L. Når vi bruker at G = mg, så blir Newtons andre lov slik
mg - L = ma
Ein enkel modell for eit fall med luftmotstand.
No vil vi prøva å finna ein modell for farten i eit slikt fall. Til det treng eit uttrykk for luftmotstanden. Spørsmålet er: korleis påvirkar farten luftmotstanden? Det er opplagt at den aukar når farten aukar, men kva er funksjonen? Vi skal sjå på den enklast mulige modellen, nemlig at den aukar proporsjonalt med farten.* Altså kan vi setja at
L = kv.
Proporsjonalitetskonstanten k vil, som forklart over, vera avhengig av
kva posisjon hopparen inntar. I tillegg spelar nok stoffet drakta er laga
i ein rolle. Newton andre lov blir då:
ma = mg - kv
Når vi huskar at akselerasjonen er lik den deriverte av farten, så kan vi
skriva dette om slik:
mv' = mg - kv
Dette er ein såkalt differensiallikning. Legg merke til at både farten v og den deriverte av farten, v', opptrer i likningen. Løysinga på ein slik likning er ikkje eit tal, slik som vanlige likningar, men eit uttrykk for funksjonen v(t). For å løysa denne likninga treng vi også å vita såkalte randbetingelsar. For oss er det at farten ved uthoppet er 0. Altså at v(0) = 0. Det kan visast at denne likninga har den generelle løysinga:
v(t) = (mg/k) + Ce(-k/m)t.
Når vi set inn at v(0) = 0, så finn vi at konstanten C = - mg/k.
Løsinga for oss er altså:
v(t) = (mg/k)(1 - e(-k/m)t)
For å finna akselerasjonen så må vi derivera v fordi a = v'. Vi får då at
a(t) = g*e(-k/m)t. Kontrolloppgave: Vis at uttrykka for v og v' stemmer med differentiallikningen over.
No kan vi også finna s(t) ved å integrera (dvs antiderivera) v(t) (Egentlig får vi også her ein konstant C, men sidan vi her har randbetingelsen s(0) = 0, kan vi finna den) Dette gir ats(t) = (m2g/k2)e(-k/m)t + mg/k*t - m2g/k2
Terminalfarten
Etter kvart som v aukar, aukar også L. Det betyr at L vil nærma seg meir og meir G. Og det betyr vidare at kraften nedover er lik kraften oppover. Når summer av kreftene er lik null, seier Newtons andre lov at også a = 0. Med andre ord akselerasjonen stoppar opp, og farten blir dermed konstant. Den hastigheten som vi har oppnådd då er terminalfarten. I vår modell er det enkelt å finna denne. Vi har at venstresida av likningen vår er 0:
0 = mg - kvt
mg = kvt
vt = mg/k
No kan vi sjå litt på korleis dette ser ut når vi set inn tal. Vi antar at m = 90kg og at k = 9. Dette gir oss terminalfarten vt = 100 m/s.
Grafane
Vi skal sjå på tre grafar der kurven for fritt fall er markert med rødt, mens løysingane våre er markert med blålilla. Dei grøne linjene representerer ein bevegelse med konstant fart lik terminalfarten. Først ser vi på ein posisjonsgraf. (posisjon - tid) altså s(t). Den blå kurven startar ut lik andregradsfunksjonen 5t2, men ganske fort nærmar den seg den retta linje markert med grønt, og som har likningen s = 100t - 1000. Denne linja har stigningstall lik 100 som er det samme som terminalfarten. Dette er ein skråasymptote.
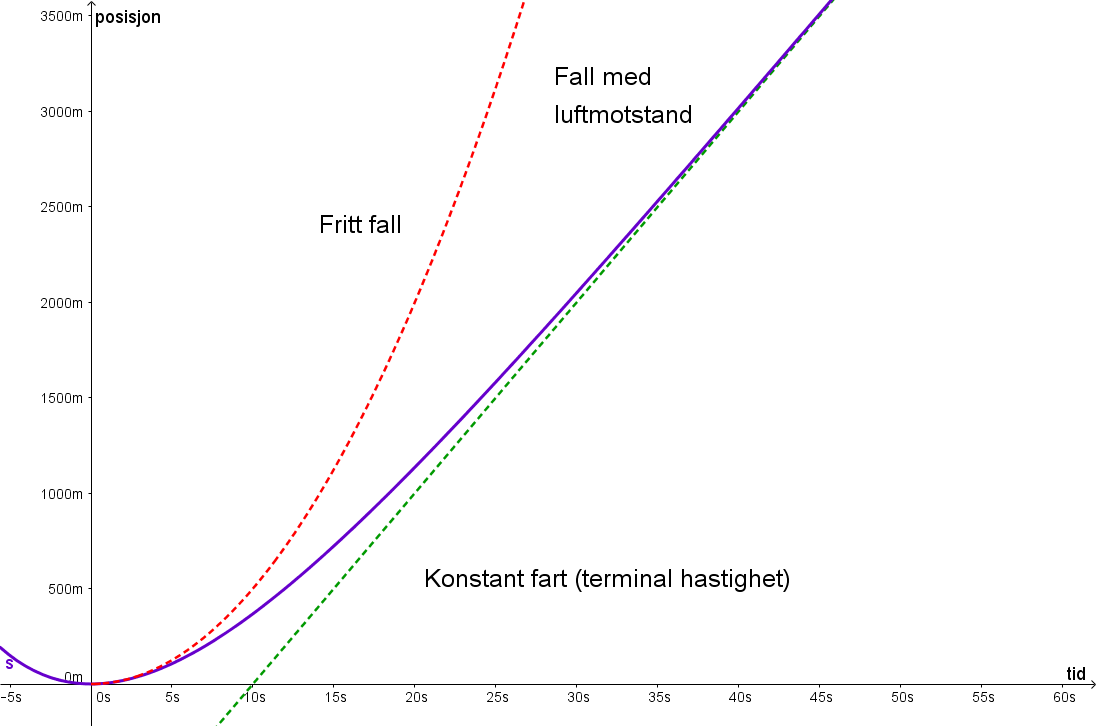
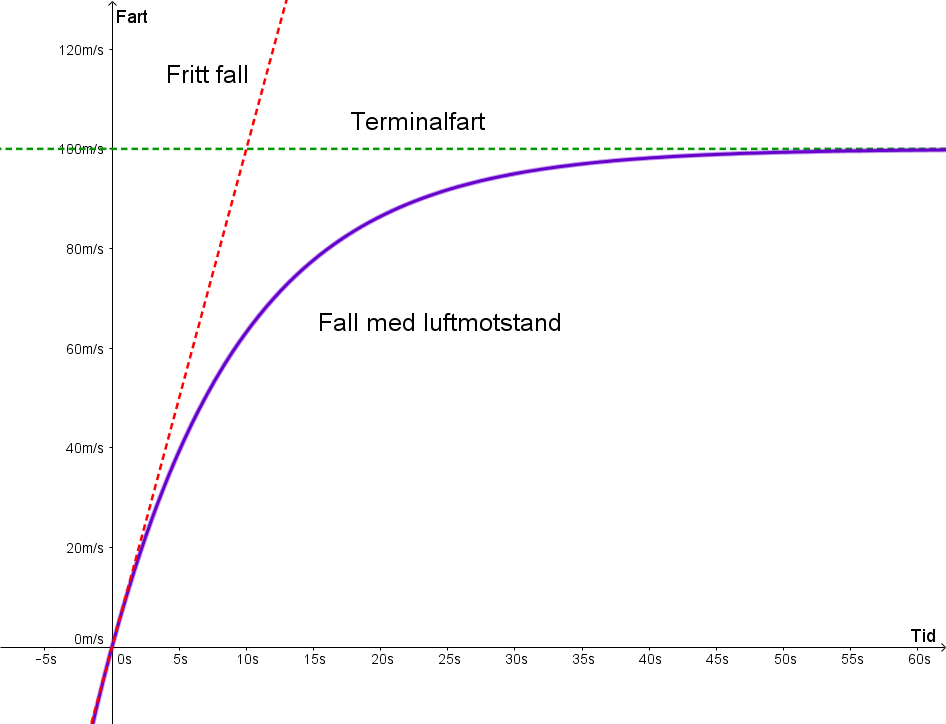
Så tar vi ein kikk på fartsgrafen. Altså v(t). Her ser vi at den
startar ut som ei rett linje. Det er den rette linja den ville fulgt uten
luftmotstand, altså linja v = 10t. Men ganske fort bøyer den av og
allerede etter 50s er den ganske nær terminalhastigheten 100 m/s, som er den
horisontale linja v = 100. Her har vi altså ein horisontal asymptote.
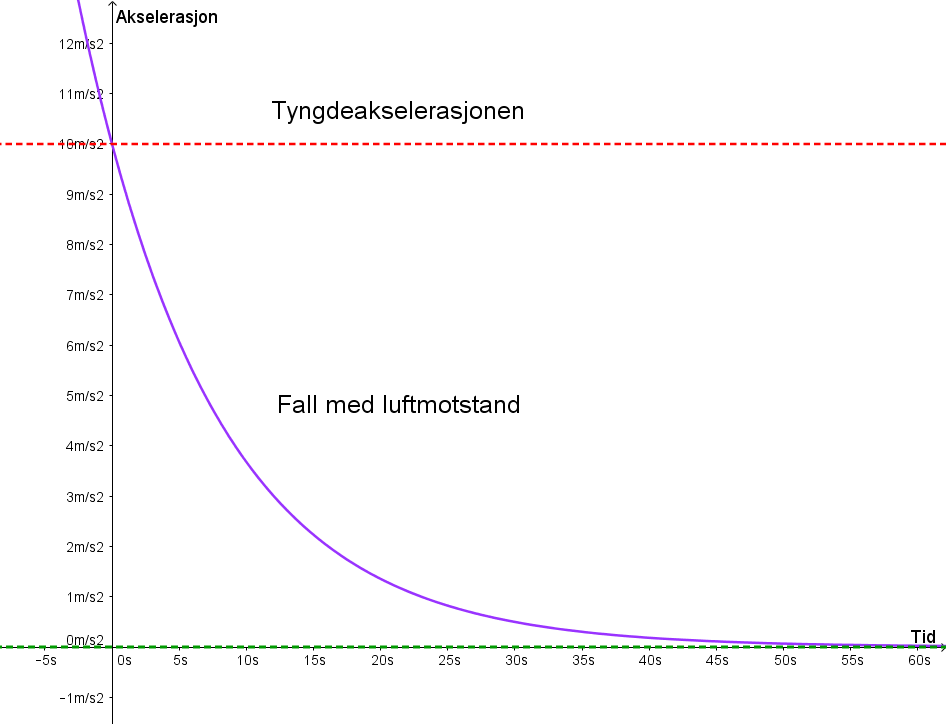
Til slutt ser vi på akselerasjonsgrafen, altså a(t). Den startar ved
t = 0, som 10, dvs det samme som tyngdeakselerasjonen. Men så stuper den
nedover og nærmar seg 0 som fortel oss at farten ikkje lenger aukar, dvs den
er konstant.
Drøfting
På alle dei tre grafane ser vi at kurven for s, v og t startar ut som grafane for fritt fall (i rødt), men det tar ikkje lang tid før dei går mot grafane som gjeld for konstant fart (i grønt). Grunnen bør no vera åpenbar: i starten er farten lav, og luftmotstanden liten. Dermed har vi i prinsippet fritt fall. Men ganske fort blir luftmotstanden nesten like stor som tyngdekrafta, og då seier Newtons andre lov at a = 0, og dermed blir farten konstant. I dei ca 50 sekunder mellom er kurvene i ein overgangsfase mellom fritt fall og konstant fart.
Andre modellar
Så spørs det kor godt modellen vår stemmer med verkeligheten. Den er nok
litt for enkel i forhold til funksjonen for L. I ein meir realistisk
funksjon for luftmotstand er:
L = kv2.
Dette gir oss ei anna differensiallikning, og andre funksjonsuttrykk for
s(t), v(t) og a(t). Vi får også ein annan verdi for k.
Men grafane til disse meir realistiske funksjonane vil likevel
likna dei vi har sett på over.
Med våre randkrav, så blir uttrykket for farten v(t) = 100 tanh(0.1t)
Då kan vi samanlikna grafane for farten:
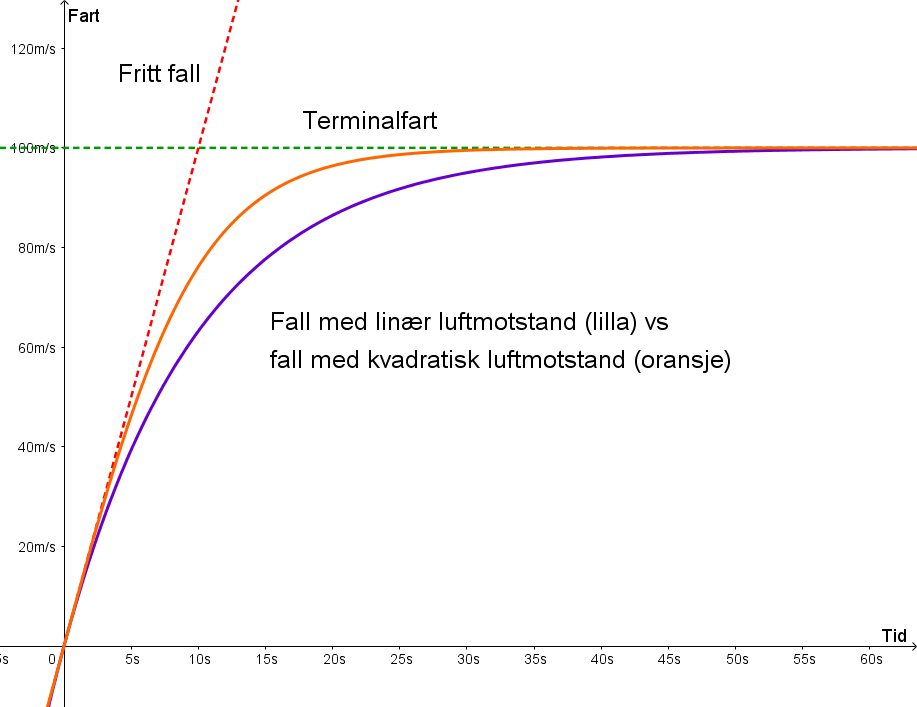
Vi ser at det tar litt lenger tid før hopparen vår merkar særlig til luftmotstanden, men så
blir virkningen veldig tydelig, slik at han får ein kraftig oppbremsing.
Så sjøl om utrekninga vår var enkel, så fangar
den inn det essensielle ved eit ufritt fall, nemlig den glatte overgangen
mellom fritt fall og konstant hastighet.
Hvis du er interessert i korleis vi kan løysa differensiallikninga for det siste eksempelet,
kan du sjå her
LENKER
http://www.batesville.k12.in.us/physics/APPhyNet/Dynamics/Newton's%20Laws/air_resistance/spsheet_solution.htm
http://oregonstate.edu/instruct/mth252h/Bogley/w02/resist.html.
wikipedia: Terminalfart
