Den deriverte
Denne artikkelen handlar om kva den deriverte av ein funksjon betyr. For ein formell definisjon må du lesa om derivasjon.
Den deriverte er det same som stigningen eller brattheten til ein funksjon. Den fortel kor bratt grafen stig på eit bestemt punkt. Ein annan måte å sei det på er at den deriverte tilsvarer stigningstalet til tangenten i dette punktet. Eit anna navn er den momentane vekstfarten* i punktet. Hvis dette var nye begrep for deg, så tar vi det sakte:
Stigningstalet til ei rett linje
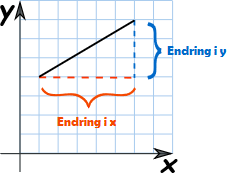
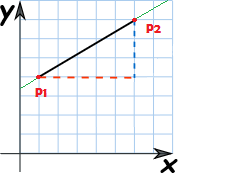
På figuren under kan vi tenkja oss at vi beveger oss frå starten av det svarte linjestykket til slutten. Då kan vi finna stigningstalet til denne linja som forholdet mellom endringen i y-verdi og endringen i x-verdi. Endringen i x på figuren er 5 og endringen i y er 3. Då blir stigningstalet lik 5/3. (ca. 1,67). Sidan endringen i y står i teljaren blir det slik at jo brattare linja går, jo større blir stigningstalet. For horisontale linjer blir stigningstalet 0, sidan endringen i y er 0. Når linja går nedover, så blir stigningstalet negativt. Men ei linje er jo uendelig. Den har ingen start eller slutt. Så korleis finn vi stigningstalet då? Svaret er at du kan sjøl bestemma kor du startar og sluttar linjstykket. Så lenge du bruker to punkt på linja. I eksempelet under passa det bra å bruka P1 og P2, fordi det var enkelt å lesa av verdiane.
Tangenten til ei kurve
Tangenten til ei kurve er ei rett linje som akkurat berører kurva i eit punkt. I dette punktet har kurva og linja same retning. På figuren er kurva "på vei ned" i punktet. Rett før punktet er også kurva nedadgåande, men ikkje så bratt. Rett etter punktet er kurva nedadgåande, og er endå brattare. Ved å tegna tangentar til kurva i andre punkt, og finna stigningstalet der, kan du finna den deriverte kor som helst på kurva under. NB: for å finna stigningstalet gjer du som over. Du treng to punkt på linja, dvs tangenten. Du kan bruka berøringspunktet som det eine, men du må ikkje.

Den deriverte er ein funksjon
På figuren under har vi tegna inn tangenten i fleire punkt og dermed funne den deriverte. Vi finn stigningstala for punkta P1, P2 og P3 som hhv. 9, - 1.92 og 0. Funksjonen her er f(x) = x3 - 3x. Vi forstår at den deriverte også er ein funksjon av x. Denne funksjonen skriva vi ofte f'(x). Ved å bruka derivasjonsreglane får vi at f'(x) = 3x2-3. Ved å setja inn x-verdiane for punkta våre kan vi rekna ut den deriverte. For P1 får vi f'(-2) = 3(-2)2 - 3 = 9. For P2 får vi f'(-0.6) = 3(-0.6)2 - 3 = -1.92, og for P3 får vi f'(1) = 3*12 - 3 = 0. Så vi ser at dette stemmer.
Vi merkjer oss at i P2, som er eit bunnpunkt, blir den deriverte 0. Det same vil vi ha i toppunktet. Fram til toppunktet er grafen stigande, og den deriverte vil derfor vera positiv. Mellom toppunktet og bunnpunktet P2 er grafen synkande, og den deriverte vil vera negativ. Etter bunnpunktet stig grafen igjen, og dermed blir den deriverte stigande.
Tolking
No har vi sett på den deriverte som brattheten til kurven. I praksis er det ofte nyttig å tenkja på den deriverte som den momentane endringen av "y" per "x-enhet". Momentan betyr i eit punkt, eller i eit øyeblikk, og y og x står i hermetegn fordi navnet på aksane og enhetene - kan vera kva som helst. Hvis den horisontale aksen står for tid, så bruker vi ofte bokstaven t, og enheten er ofte sekund, minutt, time, dag, veke eller år. Den deriverte blir då endring per tid, dvs kor fort noko endrar seg. Her er eksempel på kva den deriverte kan stå for i praksis:
- Folketal: Anta at vi ser på folketalet som funksjon av tid: N(t). Då har vi eit antalet (eit tal uten enhet) på den vertikal aksen og tid (for eksempel år) på den horisontale. Den deriverte blir då endringen i folketalet per år på et bestemt tidspunkt.
- Vekst: Tilsvarande kan vi ha feks veksten av ein plante. Då kan vi ha høyden h, i cm opp og tida t i dagar bortover. Den deriverte er då veksten per dag på et bestemt tidspunkt.
- Trykk: Anta at funksjonen vår viser trykket i atmosfæren som funksjon av høyden: P(z). Då har vi trykket P (i Pascal) oppover, og høyden z i meter horisontalt. Den derivert vil då gi oss trykkendringen per meter i ein bestemt dybde.
- Løypeprofil: Mange turrenn viser løypeprofilen med høyde i meter vertikalt og lengde i meter horisontalt. Den deriverte er då høydeendring per meter på ein bestemt plass i løypa. Dette blir ein størrelse uten enhet, som fortel kor bratt løypa er i det punktet.
- Fart og akselerasjon: Fart er endring av posisjon per tid, typisk kor mange meter ein gjenstand flyttar seg per sekund. Når vi ser på den momentane farten, eller farten på eit bestemt tidspunkt, så blir det derfor den deriverte av posisjonen: v(t) = s'(t). Tilsvarande er akselerasjon fartsendring av per tid. Momentan akselerasjon er derfor det same som den deriverte av farten: a(t) = v'(t).
* Norsk praksis er å bruka begrepet momentan vekstfart om den deriverte. Eg syns det er eit uheldig begrep sidan eg syns det passar best når det handlar om vekst.
