Samansette system

Når du skal løysa ei fysikkoppgave kan det vera lurt å setja opp ei liste over kjente og ukjente størrelsar, og gjerne også kva formlar som er relevante. Men spesielt i mekanikken er det minst like viktig å laga ein god tegning der du tegnar inn alle kreftene, både dei du kjenner og dei du antar virkar. Hvis du så skal bruka Newtons andre lov, (her forkorta til N2) så er det dessuten ikkje bare viktig, men heilt avgjerande å spørja seg sjøl: "kva gjenstand eller system av gjenstandar skal er bruka loven på?". Og då er vi inne på det som engelsktalande kallar "System of interest". Vi kan kanskje kalla det "aktuelt system".

NB: Dette begrepet "system" eller "aktuelt system" er kun eit hjelpemiddel for tanken, og har ingen fysisk realitet.

Ytre og indre krefter

Kva som er det aktuelle systemet bestemmer vi sjøl utfrå kva som er praktisk. Men det gir seg som regel sjøl av oppgava, og du vil etter kvart finna ut av det. I mange oppgaver vil det vera nødvendig å endra "system" underveis. Dei kreftene som vi må ta hensyn til i N2, er kun dei såkalte ytre kreftene, dvs dei kreftene som objekt utanfor systemet virkar med på vårt system. Indre krefter, dvs. krefter som gjenstandane inne i systemet virkar på kvarandre med, kan vi sjå bort frå. Korfor det er slik, vil bli klart i eksempelet nedanfor.

NB: Merk at begrepa ytre og indre krefter er i forhold til det aktuelle systemet du har valgt. Hvis du byter system, kan ei indre kraft bli ytre, og omvendt.

Eksempel 1

Ein bil som har massen 1200 kg dreg ei campingvogn på 400 kg. Når sjåføren gir gass bruker motoren ei kraft på 4800 N. Vi ser bort frå friksjonskrefter. Oppgava no er a) å finna akselerasjonen til bilen, og b) å finna krafta frå campingvogna på bilen.

Vi lagar tegning og identifiserer krefter. Vi kan kalla motorkrafta for K, krafta frå campingvogn på bilen for S_b og krafta frå bilen på campingvogna for S_c. Eg har brukt S fordi eg tenkjer på dei som ein form for snorkrefter. (Men du kan kalla dei det du vil). Så kallar eg massen til bilen for m_b og massen til campingvogna for m_c. Summen av disse har vi også bruk for, så den kallar eg M.

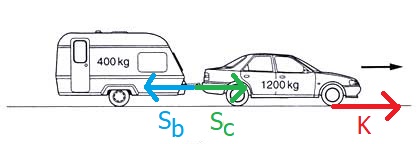
a) Vi velger først å sjå på systemet bil + campingvogn, fordi då får vi et enkelt reknestykke. Vi treng no å finna kraftsummen på dette systemet. Kreftene som virkar i horisontal retning er dei som er tegna inn: K,  S_b og S_c. I vertikal retning er det normalkrefter frå veien på hhv. vogn og bil, og det er tyngdene til bilen og vogna. Sidan vi ikkje har bevegelse i vertikal retning, må normalkreftene og tyngdene oppheva kvarandre. Derfor er ikkje disse tegna inn på tegningen. Dessuten er S_b og S_c. indre krefter, så dei kan vi sjå bort frå*. Då er det bare K som bidrar til kraftsummen. N2 anvendt på bil + vogn gir oss derfor:

K = M*a

Dette gir oss at a = K/M = 4800 N / 1600 kg = 3 m/s².

* Men du lurer sikkert på korfor vi kunne sjå bort frå S_b og S_c? Grunnen er at disse er motkrefter til kvarandre. Altså er dei like store men motsatt retta, og det betyr at dei vil summera seg til null. Alle indre krefter i eit system vil opptre i slike kraft-motkraft-par, og derfor vil dei alltid oppheva kvarandre.

b) No bytter vi system og ser på bare campingvogna. No er plutselig S_c ei ytre kraft. Og igjen vil dei vertikale kreftene nulla kvarandre ut. Så N2 anvendt på vogna åleine gir då:

S_c = m_c * a

Merk at vi kan bruka den same a som den vi fant over, for vogna og bilen heng saman og har derfor same akselerasjon. Dette gir oss då at S_c = 400 kg * 3 m/s² = 1200 N. Men no var det jo S_b som vi var ute etter. Men sidan det er motkrafta til S_c =så kan vi slå fast at S_b =1200 N. Vi kunne her ha valgt å sjå på bilen som system. Då hadde vi fått bidrag frå både K og S_c i kraftsummen, men svaret ville blitt det same. 

Eksempel 2

Ei kvinne med masse 62 kg står inne i ein heis som akselererer oppover med akselerasjonen a = 1.5 m/s².  Massen til heisen er 538 kg. Vi vil: a) finna normalkrafta frå golvet på kvinna, og b) krafta frå vaieren på heisen.

Vi tegnar inn kreftene. Her er G tyngden av kvinna, og S er krafta frå vaieren på heisen. I figuren manglar tyngden av heis + kvinne som vi kan kalla Gtot, og normalkrafta N frå golvet på kvinna ville vi vanligvis tegna med angrepspunkt under føtene, men akkurat det har ikkje så stor betydning.

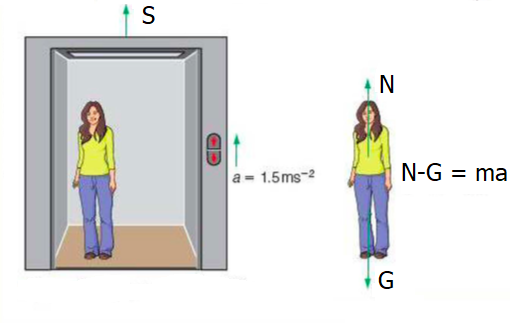
a) Aktuelt system: kvinna. Ytre krefter: normalkrafta N oppover og G nedover. N2 gir då at N - G = ma, dvs. N = G + ma. Her er G = mg, så vi får at N = mg + ma =  607.6 N + 93 N = 700.6 N.

b) Aktuelt system er no: kvinna + heisen. Ytre krefter: S oppover og Gtot nedover. Vi får då veldig lik utrekning som i stad. Forskjellen er at vi må bruka den totale massen M = 600 kg,  og den totale tyngda som blir Gtot = Mg = 600 kg * 9.8 m/s² =  5886 N. N2 gir at S - Gtot = ma, dvs S = Gtot + ma = 5886 N + 900 N = 6786 N.

Eksempel 3

Ein klosse som ligg på eit bord har massen m₁ = 2 kg.  Den blir dradd bortover av ei snor som i andre enden er festa i eit lodd med massen m₂ = 4 kg som heng frå bordkanten. Vi ser bort frå friksjon mellom klosse og bord. Snora går gjennom ei trinse som er masselaus og friksjonslaus. Vi vil a) finna akselerasjonen til loddet, og b) snorkrafta S. I figuren under er den egentlige situasjonen tegna til venstre, og så er kreftene tegna på hhv. klossen og loddet til høgre.

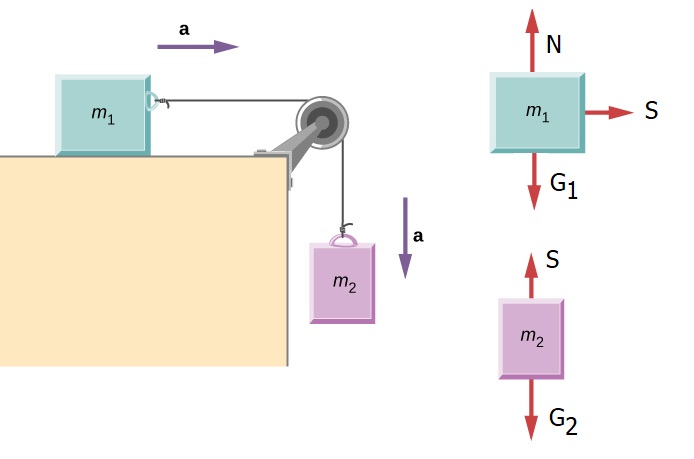
I prinsippet er dette problemet veldig likt eksempelet over med bilen og campingvogna. Vi kan tenkja på loddet som bilen og G₂ som "motorkrafta" som driv heile systemet, og vi kan tenkja på klossen som campingvogna som blir dradd. Og på grunn av at disse to heng saman så får dei den same akselerasjonen a.

a) For å finna akselerasjonen gjer vi som i 1a), og ser på kreftene på systemet klosse + lodd. Kreftene N og G₁ opphever kvarandre, og S-ane er indre krefter. (Vi har kalla begge snorkreftene S, sidan dei er like store). Når vi bruker N2 på dette systemet får derfor vi at G₂ = M*a, der M = m₁ + m₂ = 6 kg. Dette gir at a = G₂ / M = 39.2 N / 6 kg = 6.53 m/s². (Her har vi brukt at G₂ = m₂ * g = 4 kg * 9.8 m/s² = 39.2 N.)

b) Det aktuelle systemet er no klossen. Og N2 brukt på den gir at S = m₁ * a = 2 kg * 6.53 m/s² =13.06 N.

Oppsummering

Som vi ser: Dette koker ned til gjentatt bruk av N2, og når vi sørger for å konsentrera oss om å finna det rette systemet for kvar deloppgave, så får vi då ein enkel likning med ein ukjent. Vi må bare passa på å bruka riktig masse for det aktuelle systemet, og den eller dei ytre kreftene som virkar på det i bevegelsesretningen.

Du kan gjerne lesa meir om kreftene på ein bil i artikkelen Racing & Fysikk. Ellers kan du også prøva deg på gjera ei lastebiloppgave.