Normalkrafta

Når ein gjenstand beveger seg langs ei flate vil denne flata (vanligvis) virka med ei kraft på gjenstanden. Denne krafta kan vi dekomponera i ein komponent som virkar langs flata og ein komponent som virkar normalt på flata. Denne siste kraftkomponenten kallar vi normalkrafta, og vi bruker som regel bokstaven N. Grunnen til at det ofte er lurt å dekomponera slik er at når vi skal finna kraftsummen på ein gjenstand, kan vi som regel sjå bort frå N og alle andre krefter som virkar normalt på den flata gjenstanden beveger seg i, fordi vi har ingen bevegelse normalt på flata. Newtons første lov seier då at summen av kreftene i denne retningen må vera lik null.

Eksempel 1: klosse på horisontalt underlag

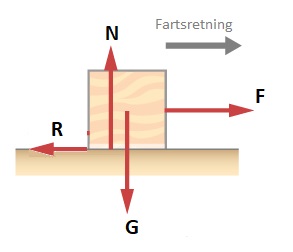
Når vi drar ein klosse på horisontal underlag er det fire krefter som virkar. Tyngden G, Normalkrafta N, Drakrafta F og friksjonskrafta R. Her er N like stor som G (men motsatt retta), og dermed er kraftsummen lik differansen F - R.

Eksempel 2: klosse på skråplan med konstant hastighet.

I figuren under har vi ein klosse på eit skråplan som er påvirka av tre krefter: Normalkrafta N, som virkar normalt på planet, Friksjonskrafta R som virkar langs planet, og tyngdekrafta G = mg, som virkar rett nedover. Vi tenkjer oss at vi har justert vinkelen θ på skråplanet slik at klossen akkurat sklir nedover uten å akselerera.

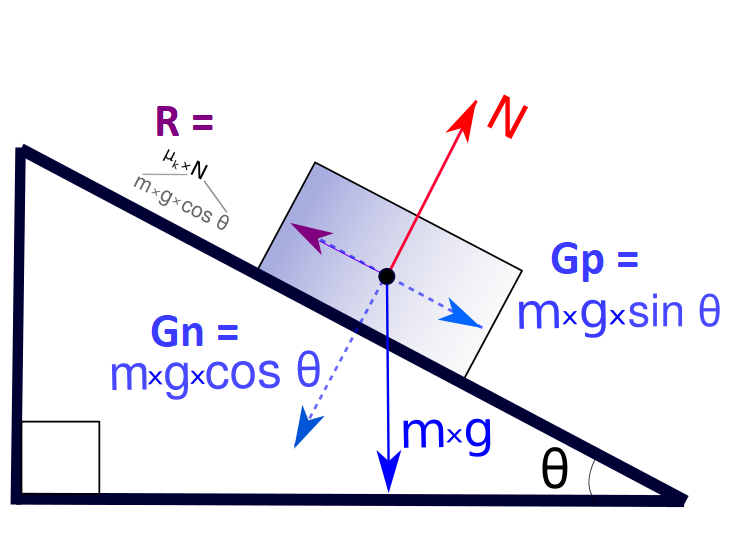
Her kan vi dekomponera G, i ein komponent Gp = mg*sin θ som går parallelt med skråplanet, og ein komponent Gn = mg*cos θ som er normalt på planet. Når vi gjer dette kan vi rekna på disse to retningane kvar for seg. I normalretningen har vi ingen bevegelse, og derfor må vi ha at N = Gn. Dette gir oss at N = mg*cos θ. Langs planet har vi konstant fart nedover, og då veit vi også at R = Gp. Sidan friksjonskrafta er gitt som R = µN, har vi at µ mg*cos θ =  mg*sin θ Her kan vi korta bort m, og hvis vi så dividerer med cos θ på begge sider får vi: µ = g*tan θ. Dette er ein vanlig måte å måla friksjonskoeffisienten i skulefysikken.