Bevegelse

I verkelighetens verden er ofte bevegelsar kompliserte og vanskelige å beskriva. Tenk bare på korleis røyken bevegar seg når du slokkjer eit lys, eller korleis fløyten beveger seg når du rører i kaffikoppen. Dette kalles turbulens. Andre eksempler på turbulens er luftbevegelsane bak eit fly eller ein bil som er i fart, og kjølvatnet etter ein båt.

Sigarettrøyk. Merk korleis røyken går frå ganske ordna bevegelse (laminær) til turbulent bevegelse.

Studerer vi små partiklar i ei væske eller ein gass med et mikroskop vil vi oppdaga at disse også beveger seg heilt tilfeldig. Dette fenomenet kalles "virrevandring" eller Brownske bevegelser. (etter den skotske botanikaren Robert Brown) Gassar og væsker er samansette system med veldig mange, bittesmå deler, og vi er som regel ikkje interessert i å beskriva kvar enkelt av disse partiklene. Ofte er vi heller interessert i gjennomsnittsfarten til atoma eller molekyla i ein gass, fordi den kan fortelja oss noke om temperaturen i gassen.

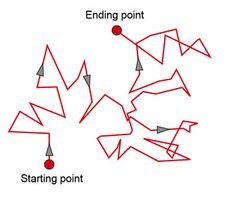
I skulefysikken konsentrerer vi oss som regel om bevegelsene til større gjenstandar som bilar, vogner, kuler osv som lar seg måla og beskriva. Men sjøl slike tilsynelatande enkle system kan være vanskelige å beskriva. Eit enkelt system som ei sol med to planeter rundt kan ha det som kallast en kaotisk bevegelse. Sjå også trelegemesystemet. Ein enkel pendel kan ofte beskrivast ganske greit, (sjå svingesystem), men også den kan ha kaotisk oppførsel hvis den blir driven av ei ekstern kraft. Sjå animasjonen Kaotisk pendel. Eit anna eksempel er å ha ein dobbeltpendel med to ledd:

Dei bevegelsane som vi ofte studerer i eit introduksjonskurs i fysikk er ordna bevegelser der enten farten eller akselerasjonen er konstant. Det første vi pleier å sjå på er lineær bevegelse, dvs. bevegelse langs ei rett linje, eksempelviser gjenstandar som fell fritt i tyngdefeltet og gjenstander som glir eller rullar på en flate eller på eit skråplan. Men generelt er fart og akselerasjon størrelsar som har både retning og verdi. Dette er det som kallast vektorar. Med vektorregning kan vi studera bevegelse i 2D, som sirkelbevegelser, skrått kast i tyngdefeltet eller satelittbevegelsar rundt jorda.

Definisjonar

For å beskrive ein bevegelse treng vi å definera noken fysiske størrelsar. Grunnstørrelsane vi treng er tid og posisjon. Frå disse to definerer vi fart, og frå fart og tid får vi akselerasjon.

Fart

Vi skal starta med å definera fart. Men det fins to typar fart. Den første typen er gjennomsnittsfarten, som er lik den tilbakelagte distansen Δs dividert med den tida Δt som er brukt:

Merk at vi ofte bruker strek over v-en for å skriva gjennomsnittsfart. Den andre typen er øyeblikksfarten, eller det som vi i fysikk kallar momentanfarten. Den matematiske definisjonen er den grensa som gjennomsnittsfarten går mot når vi lar Δt gå mot null, dvs:

I praksis er vi ofte fornøyd med å la Δt og Δs vera små. For eksempel kan vi måla farten til ein bil over ein distanse på eit par-tre meter. Les meir om fartsmåling.

Akselerasjon:

Her er det også to typar. Vi snakker for det første om gjennomsnittakselerasjon, som er den endringen i fart, Δv, som har skjedd i løpet av tida Δt, altså:

Her brukar vi også strek over a-en når vi snakkar om gjennomsnittakselerasjon. Og på same måten som for fart, definerer vi øyeblikksakselerasjonen eller momentanakselerasjon, som grensenverdien når Δt går mot null, dvs.

Her vil vi også i praksis vera fornøyd med bruka to fartsmålingar som er ganske nær kvarandre. Enheten for akselerasjon blir m/s² (meter per sekund per sekund) sidan vi dividerer enheten for fart (m/s) på tid (s).

Bevegelsesformlane

For å rekna på bevegelsar treng vi formlar. Det enklaste tilfellet er konstant fart, og den einaste formelen du treng då er s = vt. Eller, hvis bevegelsen ikkje startar frå origo men i s₀, kan vi bruka formelen s = s₀ + vt.

Det nest enklaste er konstant akselerasjon. Her er det fire formlar du treng å kunna.

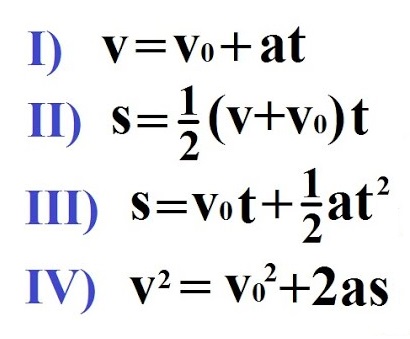
Formel I kallast fartsformelen. Formel II og III kallast veiformel 1 og 2, og formel IV kallast "den tidløse formelen". Vanligvis er det viktigast å kunna bruka disse formlane til utrekningar, men det skadar ikkje å kunna utledningane også.

Grafisk framstilling

I tillegg til å bruka disse bevegelsesformlane, er det også nyttig å bruka ulike grafiske fremstillingar. Det er tre ulike typer grafar som vi ofte brukar: veigraf, fartsgraf og akselerasjonsgraf.

Å finna fart frå veigrafen.

Hvis vi har målt veldig mange posisjonar kan vi laga ein veigraf, som då viser posisjon som funksjon av tid, altså s(t). Når vi skal måla ein gjennomsnittsfart, så måler vi posisjonen ved to ulike punkt P₁ = (t₁, s₁) og P₂ = (t₂, s₂). Då kan vi rekna ut Δs = s₂ - s₁ og Δt = t₂ - t₁. Gjennomsnittsfarten er altså lik forholdet Δs/Δt, og grafisk er dette det same som stigningstalet til linja gjennom P₁ og P₂, som er markert med grønt i figuren til venstre under.

For å finna momentanfarten, så merkar vi oss at definisjonen egentlig seier at farten er den deriverte av posisjon, dvs. v(t) = s'(t). Det betyr at momentanfarten kan finnast som stigningstalet til tangenten i punktet vi måler i. Tangenten er den grøne linja i figuren til høgre under.

Fart fra veigrafen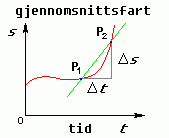

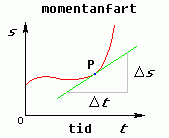Å finna strekning frå fartsgrafen

Når vi tegnar funksjonen v(t), så får vi ein fartsgraf. Sidan farten er den deriverte av posisjon, så kan ein visa at tilbakelagt strekning er lik det bestemte integralet v(t). Grafisk er dette lik arealet under grafen mellom dei vertikale linjene som definerer start og slutt for bevegelsen. Dette gjeld generelt som vist i figuren til venstre under.

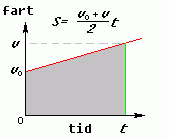
For det tilfellet at vi har konstant akselerasjon, så vil farten vera gitt som v(t) = v₀ + at. (Frå formel I over). Dette er då ei rett linje, som viste i figuren til høgre under. I dette tilfellet kan vi rekna ut arelet vha formelen for eit (liggande) trapes. Så vi summerer høydene v₀ og v og deler på to, og så mulitpliserer vi med breddem som her er lik t (t₀ = 0). Dermed får vi veiformel II!

strekning fra fartsgraf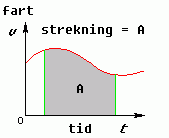

Grafane for konstant fart og konstant akselerasjon

Under har vi vist veigraf, fartsgraf og akselerasjonsgraf for dei to tilfella konstant fart og konstant akselerasjon.

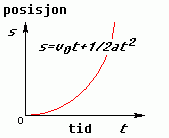
Veigrafane: For konstant fart blir veigrafen ei rett linje med stigningstal v, mens veigrafen for konstant akselerasjon blir ein andregradsfunksjon gitt ved formel III. Når akselerasjonen er positiv vil denne grafen venda den hule sida opp, slik figuren under til høgre viser.

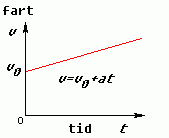
Fartsgrafane: konstant fart betyr at v ikkje endrar seg, og grafen er då ei flat linje. Grafen for konstant akselerasjon er, som diskutert over, ei rett linje med stigningstal lik a, og vi legg merke til at den startar i v₀.

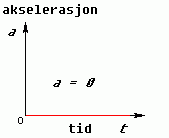
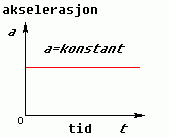
Akselerasjonsgrafane. Konstant fart betyr at det er ingen akselerasjon, dvs. a = 0. Konstant akselerasjon gir ei horisontal linje.

	konstant fart	konstant akselerasjon
veigraf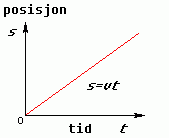
fartsgraf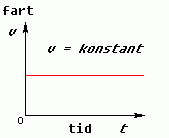
akselerasjons- graf