Luftmotstand er den krafta som lufta utøver på gjenstandar som beveger seg gjennom lufta. Ein snakkar også om væskemotstand, som i prinsippet er det same. På engelsk bruker ein meir generelt uttrykket Drag, som ein samlebetegnelse på den motstanden ein gjenstand møter når den beveger seg gjennom ei væske eller ein gass. Denne artikkelen er meint å vera første førstehjelp for enkle simuleringar med luft- og væskemotstand, men dette eit stort og komplisert felt, og vi berører bare overflata her. Luftmotstanden virkar alltid mot den relative bevegelsen til gjenstanden. Med andre ord må vi sjå på farten til gjenstanden i forhold til lufta. Det betyr at noken gonger bremsar den, andre gonger akselererer den. Hvis vi kastar ein ball med 5 m/s, og den samtidig har ein medvind på 10 m/s, så er den relative farten 5 m/s bakover. Så krafta frå lufta vil i dette tilfellet virka framover. Hvis medvinden var mindre enn 5 m/s, eller motsatt av gjenstandens bevegelse, så vil også luftmotstanden virka mot bevegelsesretningen.
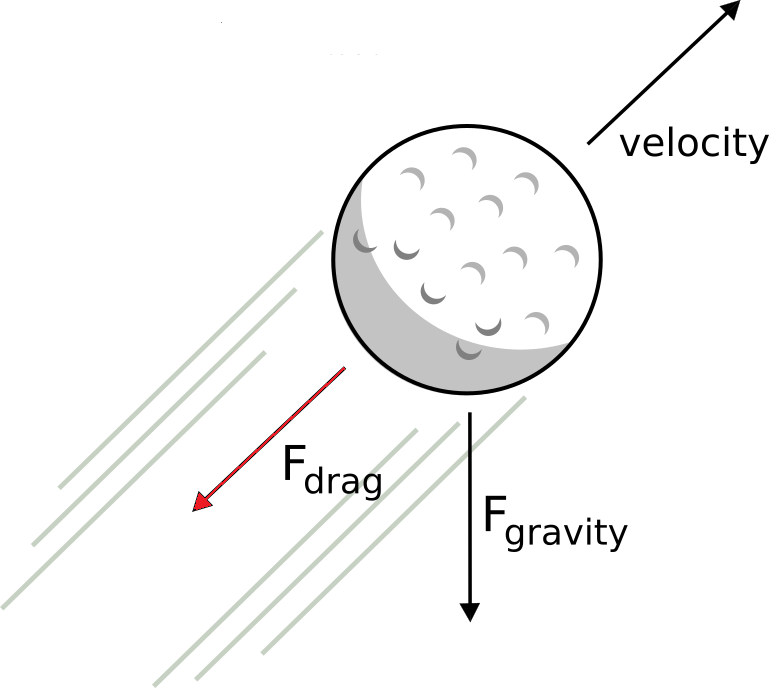
Noko av motstanden skuldast friksjon mellom overflata til
gjenstanden og lufta eller væska som strøymer langs den. Ein annen del av
motstanden skuldast forskjellen i trykk i luften eller væska
framfor og bak gjenstanden. Bak gjenstanden blir det danna virvlar, og i
virvlane er det undertrykk. Summen av trykkreftene på hele gjenstanden
blir derfor retta mot bevegelsesretningen.
Luftmotstanden aukar med hastigheten. Derfor vil gjenstandar som fell,
etter kvart få konstant fallhastighet. Dette kallast terminalhastigheten.
Ein fallskjermhoppar kan oppnå ein fart på omkring 50 m/s før skjermen er
folda ut. Regndråper har en fart i forhold til lufta på nesten null for
dei minste dråpane til bortimot 10 m/s for dei største. Les meir om fall.
Lovene for luftmotstand er i stor grad eit resultat av eksperiment. For simuleringar av kast og liknande, er det to formlar som er aktuelle. Ein som gjeld for lave hastigheter, og ein som gjeld for høge.
I lave hastigheter er det friksjonen som dominerer. Strømningen rundt gjenstanden vil då vera jevn og uten virvlar, såkalt laminær strømning. Her gjeld den såkalte Stokes lov som seier at motstanden er proporsjonal med hastigheten v. For ein kuleforma gjenstand kan vi skriva den som:
FD = 6πη ·r ·v, der r er radiusen til kula, v er hastigheten og η er viskositeten.
Viskositet er eit mål for "seigheten" til ei væske. For eksempel er viskositeten til vatn er høgare enn luft, men lavare enn for olje. Viskositeten har fleire betydningar, og for å vera meir presis, så er det den dynamiske viskositeten som inngår i formelen. Viskositeten er ikkje bare avhengig av mediet, men også temperaturen til mediet. Sjå eksempel på dette her. Ein omtrentlig verdi for vatn er 1 · 10-3 Ns/m2 , for luft ca. 1.8 · 10-5 Ns/m2. Men disse verdiane varierer med temperaturen, og det fins online-kalkulatorar som gir deg betre verdiar ved ulike temperaturar både for luft og for vatn. Verdien for olje varierer med typen, og kan vera alt frå 0.005 til nærmare 4. Sjå tabell.
I praktisk simulering vil ein samla alle disse konstantane til ein, feks. kan vi setja k = 6πη ·r, og dermed få den enklare formelen:
FD = k·v
I høge hastigheter er det trykkmotstanden som dominerer. Her vil strømningen rundt gjenstanden vera turbulent. Krafta er gitt ved den såkalte "Drag equation":
der:
CD er dragkoeffisienten for gjenstanden. Denne er
avhengig av både formen til gjenstanden og egenskapar ved overflata. For
ei kule kan den variera frå 0.07 til 0.5
ρ er mediet (gassens eller væsken) sin tetthet
. Vatn har tetthet 1 kg/m3, mens for luft er den omtrent
1.2 (kg / m3)
A er arealet av det tverrsnittet av gjenstanden som står normalt
på (på tvers av) strømningsretningen. Merk at dette kan variera, dersom
objektet forandrar posisjon i forhold til luftstraumen. For fly skjer
dette dersom vi endrar på angrepsvinkelen.
v er gjenstanden sin relative hastighet i forhold til mediet
(gassen eller væska).
Det korte svaret er at i dei fleste praktiske anvendelsane er det den turbulente, dvs. andregradsregelen som gjeld. Den hastigheten der regelen for "høge" hastigheter gjeld er som oftest veldig lav, derfor hermetegna. Eksempelvis er grenseverdien for ein fotball med diameter 22cm, omtrent 0.068 millimeter per sekund i luft, og 0.0045 mm/sek i vatn.
Når det gjeld fly og rakettar, så snakkar ein om andre typar motstand, som indusert motstand, som oppstår når eit fly utvikler løft. Sjå artikkel om aerodynamikk.
Når vi skal bruka formel 2 over, treng vi eit estimat for CD. Det beste er sjølsagt å gjera din egen måling, men i mangel av det, kan du sjå litt på typiske verdiar under.
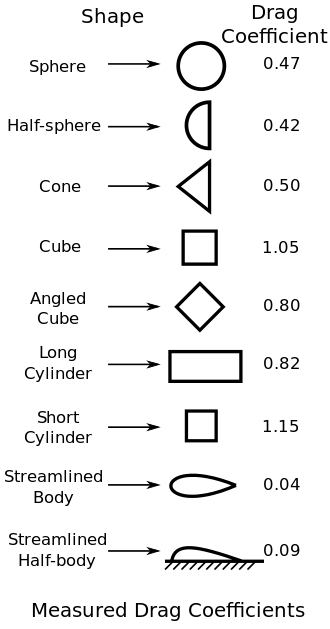
Andre eksempel på dragkoeffisientar, funne her, og andre stader. Merk at disse tala har stor usikkerhet, og at ulike kjelder oppgir forskjellige verdiar. Med andre ord: for ein bestemt gjenstand, så må ein gjera målingar sjøl!
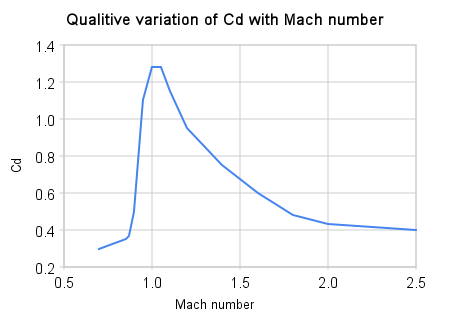
Men er egentlig CD konstant? Nei! Når farten nærmar seg 0.8*lydhastigheten (Mach 0.8) bryt likningen over saman. Men hvis vi insisterer på å bruka CD, så betyr det at den ikkje er ein konstant, men varierer med farten. Slik kan den sjå ut frå litt under lydhastighet til Mach 2.5:

For skyting med prosjekttiler, så fins det kurver som er utrekna for standardprosjekttiler med ein bestemt form. Dette er den såkalte G-modellen, som gir Cd som funksjon av v, for ammunisjon kategorisert etter sju typer kalla G1, G2, G5, G6, G7, G8 og Gl. Her er data i tabellform.
Luft er ein gass som kan komprimerast. Og i atmosfæren er det stabla lag på lag med luft oppå kvarandre, så blir dei nederste laga trykt saman. Dette betyr at tettheten minkar med høyden. Ved bakken, er tettheten omtrent 1.225 kg per kubikkmeter. Den varierer med temperatur og trykk, men dette er standardverdien ved 15 grader. I tusen meters høyde fell verdien til omtrent 0.4135 kg/m3, og i 20 000m er den 0.08891 kg/m3. Går vi heilt opp til 80 000 m er tettheten 0.00001846 kg/m3, og det er forsvinnande lite luft igjen. Ein er ikkje heilt enige om kor grensen for atmosfæren går, men dette er langt over det vanlige fly kan operera i, og høgt nok til at det begynner det å bli mulig å ha satelittar i bane. Med andre ord, der sluttar luftfarten og romfarten overtar. Hvis vi brukar data frå tabellen i U.S. Standard Atmosphere, og gjer ein regresjonsanalyse, så finn vi at tettheten går omtrent som 1.225 * 0.9998964y. Så dette er ein formel vi kan bruka når vi skal simulera prosjektiler i høge banar.
Wave drag. (for mach 8 og høgare)
The drag coefficient (NASA)
Causes of aerodynamic drag. (Trykk og friksjon)
Aerodynamic Drag of Contemporary Soccer Balls.
Tennis Ball Trajectories Aerodynamic Drag and Lift in Tennis Shots.
Review of tennis ball aerodynamics.