Arkimedes
Arkimedes var født ca. 287 fKr i Syrakus på Sicilia, og døydde same stad i år 212/211. Arkimedes er nok mest kjent for (angivelig) å ha hoppa ut av badet og springa naken gjennom gatene og ropa "Eureka! Eureka!" ("Eg har funne det"), og for sine oppfinnelsar som Arkimedes sin skrue, men det er hans matematiske verk som er dei mest imponerande.

Oppfinnaren Arkimedes
Arkimedes sin skrue er ein smart innretning for å pumpa opp vatn. Det
blir sagt at han konstruerte denne for å irrigera dyrkbare deler av
nildalen, og det er ikkje umulig sidan han hadde kontakter i Alexandria.
På den andre sida kan det henda at det var nettopp i Egypt at Arkimedes
lærte dette. Uansett er det ein nyttig dings, som blir brukt den dag i dag. Ein annan historie kan
fortelja at den vart brukt til å lensa skipet Syracusia, som skal ha vore det største skipet på
den tida. Noken seier også at Arkimedes var ingeniøren bak dette skipet.
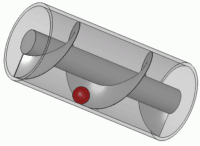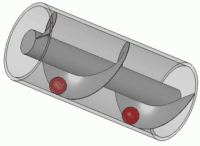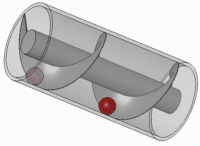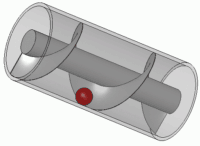
Figur laga av Silberwolf CC BY-SA 2.5
Ein annan, og meir tvilsom oppfinnelse, er den såkalte dødsstrålen hans. Ei forteljing går ut på at omkring år 212, då Syrakus var beleira av romarane under punerkrigen, laga han eit, eller mange, store speil, som reflekterte og samla strålene frå sola, slik at romarane sine skip vart sett i brann.

Noko slikt høgst usannsynlig, og har blitt tilbakevist av mellom andre Mythbusters. Kanskje ikkje like usannsynlig, men likevel tvilsom er kloa til Arkimedes. Dette skal ha vore ein slags kran som kunne ta tak i fiendtlige skip og få dei til å kantra. Enten noko av dette er sant eller ikkje, er det absolutt mulig at Arkimedes konstruerte andre smarte våpen som var brukt mot romarane. Noken meiner for eksempel at dødsstrålen kan ha vore ein form for gassdrive kanon.
Men sprang han naken?
Etter som soga går, skal Arkimedes har fått i oppdrag av kongen av Syrakus, Hieron II, å finna ut om gullkrona hans verkeleg var av gull. Då Arkimedes la seg i badekaret, la han merke til at vatnet steig høgare. Så han fant då ut at det bare var å senka krona ned i vatn, og måla kor mykje det steig, så kunne han finna volumet av den. Og når han også kunna måla vekta, så kunne han finna massetettheten. Og hvis den massetettheten var like stor som for gull, så var det gull! Men var dette så mykje å ropa hurra (eller Eureka) for? Neppe! Ingen ringare enn Galileo Galilei meinte at dette var sludder og pølsevev. For det å måla volum med stor nøyaktighet var nemlig ikkje så lett på Arkimedes si tid. Det Galielo meinte var mykje meir sannsynlig, var at Arkimedes brukte sitt eget prinsipp om oppdrift, nemlig at oppdriften er lik tyngda av den væskemengden som gjenstanden fortrenger. Så ein ting som blir vegd i vatn blir lettare med ein verdi som er proporsjonal med volumet. Dermed, sa Galileo, kunne ein finna ein gullklump som var like tung som den antatte gullkrona ved å vega dei med ei skålvekt. Deretter kunne ein senka både krona og gullklumpen ned i vatn og vega dei på nytt. Hvis vekta fremdeles var i balanse, så betydde det at oppdriften var identisk, og dermed at volumet av krona og gullklumpen var like. Det betyr igjen at dei har same massetetthet, og dermed er av same stoff. Det ville Arkimedes kanskje ha ropt Eureka for.
Matematikaren Arkimedes
Men sjøl om han faktisk oppfant disse krigsmaskinane, så er det for ingenting å rekna i forhold til det han gjorde innan matematikken. Og for å hindra at andre gav seg ut for å vera antikkens største matematikar, dvs. han sjøl, så fant han ein lur måte å avsløra juksepavar. Blant dei greske matematikarane var det vanlig å annonsera nye teorem uten bevis. Men Arkimedes kunne då også putta inn to eller tre proposisjonar som var usanne, men som krevde heile hans matematiske talent for å motbevisa. Når falsknarar påsto disse som sine egne, kunne han lett avsløra dei med eit moteksempel!
Arkimedes sine arbeid kan delast i tre grupper
- Statikk, hydrostatikk og flytande gjenstandar, som feks den nevnte loven om oppdrift
- Diverse arbeid om teljemåtar og notasjonar. I verket Psammites (Sandteljaren) skrytte han av at han kunne skriva eit tal som var større enn antal sandkorn i universet.
- Bevis for teorem angåande areal og volum.
Omfanget av dette arbeidet er enormt, men mange av hans originale verk er gått tapt. Likevel er ein heil del av dei blitt bevart gjennom arabiske oversettelsar. Dessuten har vi den såkalte Arkimedes-palimpsesten (eller kodeksen).
Arkimedes-palimpsesten
Ein palimpsest er eit dokument som er skrapa og overskrive igjen. Dette var ikkje uvanlig på den tid, sidan papyrus og pergament var vanskelig å skaffa. I 1906 fant den danske filologen Johan Ludvig Heiberg (1854–1928) i Konstantinopel eit gresk matematisk manuskript som var overskrive med bøner på latin. Dette var Arkimedes’ «Metoden for mekaniske satser», eit brev som Arkimedes skreiv til sin venn Eratosthenes der han gjorde rede for korleis han hadde funne fram til fleire av sine resultater. Slik ser ei side av den ut:

Arkimedespalimpsesten er skanna, og fins online på OPenn (Eit digitalt arkiv ved Universitetet i Pennsylvania).
Sandteljaren
I verket Sandteljaren henviser Arkimedes til Aristarkos frå Samos som hadde foreslått at jorda gjekk i bane rundt sola og ikkje motsett, altså den heliosentriske modellen. Men problemet med denne teorien var at i såfall skulle ein kunna observera endringar i stjernene sine posisjonar i forhold til kvarandre. Men dette hadde ingen observert, og det var ikkje før etter Galielo og Copernicus si tid at dette kunne observerast. Grunnen er, akkurat som Arkimedes hevda, at avstandane er så store at det er veldig vanskelig å sjå. Men grekarane hadde ikkje eit talsystem som kunne brukast for slik astronomiske størrelsar. Så Arkimedes sette seg fore å laga eit som kunne brukast for å telja sandkorn i universet. Dermed fant Arkimedes opp ein skrivemåte basert på myriaden M, som var 10 000. Ved å bruka det som base kunne han ikkje bare uttrykkja tal som ein myriade myriader, dvs 108, men også ein myriade opphøyd i ein myriade, dvs. MM. Det største talet han nevnte var MMM som er eit ett-tal fulgt av åtti billionar (80·1015) nullar. Arkimedes sitt system minnar om eit posisjonssiffer-system med base 108, noko som er bemerkelsesverdig i og med at grekarane på den tid ikkje eingong hadde eit vanlig posisjonssiffer-system. Verd å merkja seg er også at for å rekna med slike store tal, fant han regelen for eit produkt av potensar, dvs: 10a *10b = 10a + b. Han var med andre ord godt på vei til å oppdaga logaritmane.
Måling av sirkelen
Eit av dei mest berømte verka av Arkimedes i middelalderen var Måling av sirkelen. Her viser han at forholdet mellom omkretsen av ein sirkel og diameteren (det vi i dag kallar π) er mindre enn 3 og 1/7 og større enn 3 og 10/71, som er ein ganske god tilnærming til pi. Han var med dette den første som rekna på pi, og han gjorde dette ved å bruka ein innsnevringsmetode. Han sa at omkretsen av sirkelen måtte vera mindre enn omkretsen til ein omskriven regulær mangekant og større enn omkretsen til ein tilsvarande innskriven mangekant. Sjå figur under:
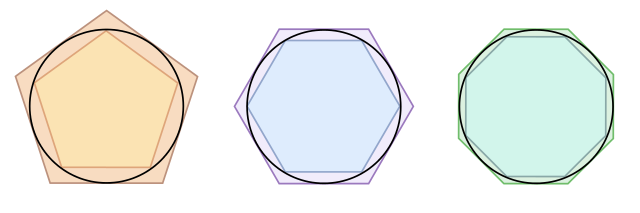
Ved å først rekna ut for ein sekskant, kunne han så dobla antal kantar, og rekna ut for ein tolvkant, osv. til han enda opp med ein 96-kant, og fant sitt estimat. Med dette fant han ikkje bare eit betre tall for pi enn nokon før han, men også ein algoritme som gjer at du kan finna talet pi med så stor nøyaktighet du vil. Slik har han også vist at han forsto begrepet grenseverdi. Les meir om dette i Pi à la Arkimedes.
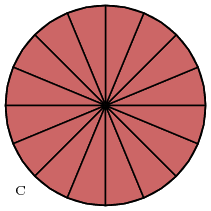
I det same verket viser Arkimedes også at arealet av ein sirkel er lik arealet av ein trekant med høyde lik radien i sirkelen, og lengde lik omkretsen. Med moderne notasjon kan vi skriva det som at A = 1/2 * r * 2πr = πr2. Vi kan sjå at dette stemmer (men det er ikkje eit ordentlig bevis) ved å dela sirkelen inn i sektorar som vi kan reorganisera, først ved å "rulla dei ut", og deretter ved å forskyva toppane:
 tilsvarer
nesten
tilsvarer
nesten 
Hvis vi drar alle toppane til venstre slik at dei samlar seg i same punkt, så har vi ikkje endra arealet av dei. (Husk at arealet av ein trekant er lik 1/2 * grunnflate * høyde, og høyden er ikkje endra når vi drar toppane til venstre.

Eit anna resultat som viste Arkimedes sitt geni var å finna arealet av eit såkalt eit parabelsegment, dvs området mellom ein parabel og ei linje som skjer denne. Metoden hans var å dela arealet inn i trekantar som han så auka i antal mot uendelig. Les meir om dette i Parabelens kvadratur. Her har han i same slengen også funne summen av ei uendelig (og konvergent) rekkje.
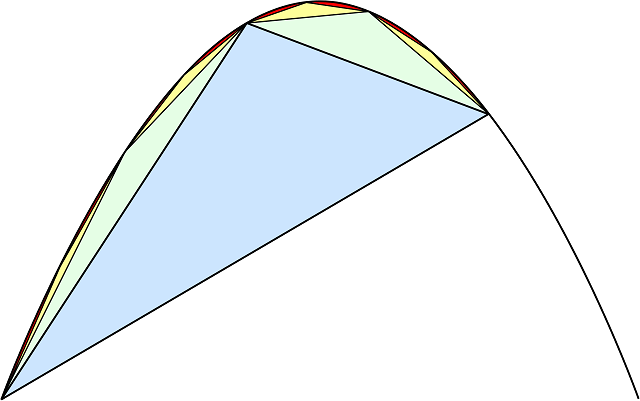
Dette er jo (nesten) ein form for integralrekning. Og kor nær han kom integral kalkulus ser vi i den metoden han brukte for å finna volumet av ei kule (i forhold til ein sylinder). Eudoxus hadde tidligare vist at ei kjegle har ein tredjedel av volumet til ein sylinder med same grunnflate og høgde. Arkimedes fant ut at volumet av ei kule med same radius /og høgde 2r) var 2/3 av sylinderen. Altså kan vi setja opp følgande "likning":
Ein annan måte å skriva opp dette resultatet er at volumet av ei kule er 4/3 π r3. Arkimedes gjorde dette med å finna opp ein metode som seinare vart gjenoppdaga som Cavalieris prinsipp. Dette involverer å slaisa opp romfigurar på samme måten som vi skjer opp ein salami. Så hvis vi tenkjer oss ein blå sylinder (salami) med eit kuleforma hulrom, så vil slaisane sjå slik ut når vi begynner å kutta frå toppen:

Arven etter Arkimedes
Arkimedes døydde under beleringa av Syrakus. Han vart myrda av ein romersk soldat, til tross for at hans kommandant, general Marcellus hadde gitt ordre om å spara han. Den romerske skribenten Cicero skal ha besøkt grava hans eit hundreår seinare, og fortel om ein gravstein der det var rissa in ei kule og ein sylinder. Det er sagt at Arkimedes hadde bedt om dette som eit minnesmerke over det han sjøl rekna som sin største matematiske oppdagelse. Det er også sagt at Arkimedes sine siste ord var «Ikkje rør sirklane mine» (på gresk: μή μου τούς κύκλους τάραττε, og på latin: Noli turbare circulos meos). Det fins ikkje pålitelige bevis for dette, men heilt usannsynlig er det ikkje :)
Det er på sin plass her å minna om at alle dei store i matematikken måtte finna på teorem, ord og notasjonar etter som kvart som dei hadde behov for det. For eksempel fant Arkimedes opp sin berømte spiral for å kunna tredela ein vinkel. (Eller gjorde han det?) Her kan du kan sjå ein fiks GeoGebrasnutt om dette, og beviset kan du sjå her. Arkimedes hadde jo så mykje mindre å starta med enn dei som kom etter, men likevel kom han så langt! Rett nok var det ikkje om Arkimedes at Isaac Newton sa "Hvis eg har sett litt lenger, så er det ved å stå på skuldrane til kjemper", (Det var til Robert Hook) og rett nok var det heller ikkje Newton som sa dette først, men det passar likevel minst like bra. For arbeidet til Arkimedes la grunnlaget for at Newton, Leibniz og andre kunne utvikla den moderne infinitesimal- og integralrekninga, dvs det vi i dag kallar Kalkulus (eller matematisk analyse).
LENKER
Archimedes på Encyclopedia Britannica
Archimedes: The Original Naked Scientist. :)
Archimedes: inventor of war machines and calculus (almost)
Archimedes on the Circumference and Area of a Circle
Archimedes and the Volume of a Sphere
Archimedes Palimpsest Wikipedia
Bla i "The Works of Archimedes" redigert av by T. L. Heath
