Parabelens kvadratur
Over to hundre år før vår tidsrekning fant den store matematikaren og ingeniøren Arkimedes ut ein setning som i seg sjøl kanskje ikkje er så oppsiktsvekkjande i dag, men som likevel var med å leggja grunnlaget for den moderne integral- og infinitesimalrekninga. Og seinare kunne folk som Newton, Leibnitz med fleire byggja vidare på hans metodar for å utvikla det som kallast kalkulus (eller matematisk analyse).
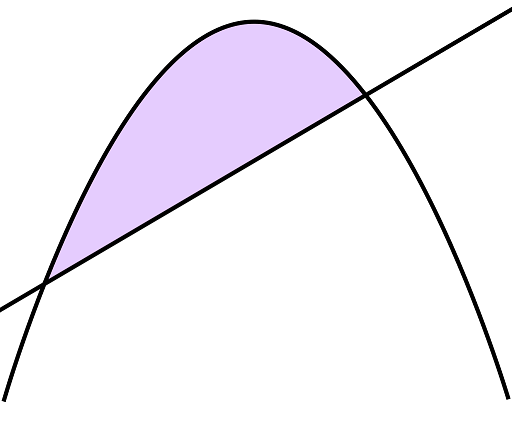
Det Arkimedes fant ut var at arealet av eit parabelsegment er 4/3 gonger arealet av den innskrivne trekanten. Eit parabelsegment er området mellom ein parabel og ei linje som skjer denne, som vist under til venstre. Den innskrivne trekanten er vist til høgre. Det Arkimedes påstår er altså at det lilla arealet er 4/3 gonger det blå.
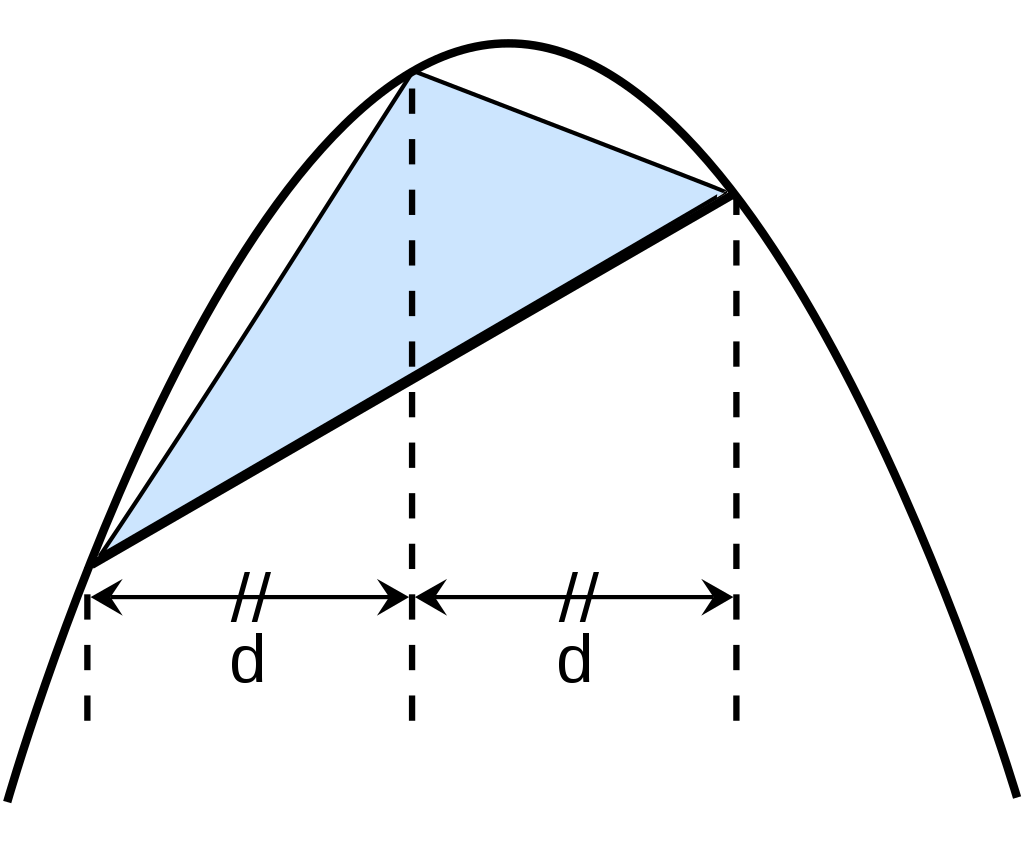
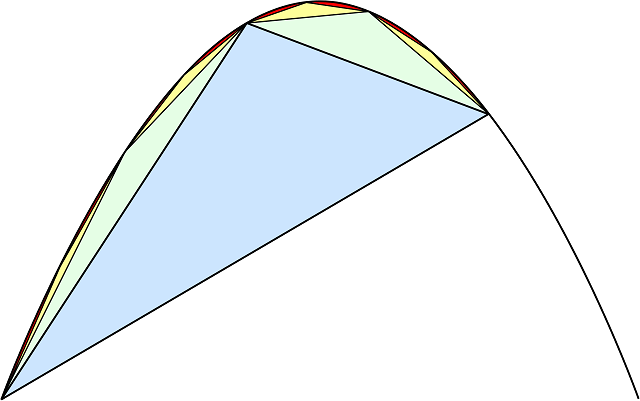
Måten Arkimedes brukte for å finna ut dette, var å dela opp parabelsegmentet i stadig mindre trekantar, og finna ein sum for dette. Han starta med den blå trekanten under, som ein tilnærming til det arealet han skulle finna. Så la han til to nye trekantar (dei grøne), og deretter dei fire gule. Hvis vi fortset slik i det uendelige vil summen av alle trekant-areala bli lik arealet av dette parabelsegmentet som vi er ute etter. På denne måten kunne han ikkje bare finna eit så nøyaktig tal som han trengte, men han klarte å finna det eksakte svaret når vi summerer uendelig mange ledd! Vi skal her sjå korleis kan klarte dette.
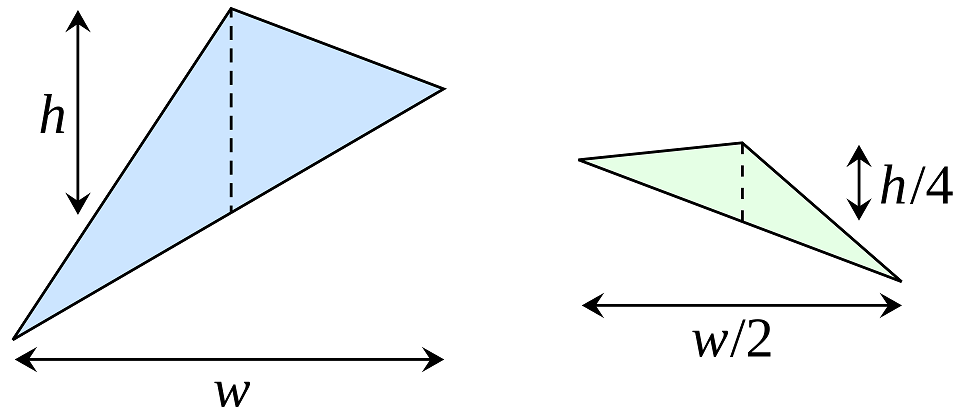
Vi ser først litt nærare på den blå trekanten og ein av dei grøne. Og så innfører vi bredder og høyder i trekantar som ikkje er vanlige. La oss sei at bredden w er utstrekningen til trekanten i x-retningen, og høyden h er avstanden i y-retning frå toppunktet og loddrett ned på grunnlinja, som vist på figuren under. Arealet av den blå trekanten er då w * h / 2. Toppunktet er plassert slik at x-koordinaten er midtveis mellom x-verdiane til ytterpunkta. Det betyr at bredden til den grøne trekanten er w/2. Sidan toppunkta til dei nye grøne trekantane ligg på parabelen, kan det visast at høyden i den grøne trekanten er h/4. Og det betyr at arealet til den grøne trekanten er (w/2 * h/4) / 2. Altså er kvar av dei grøne trekantane 1/8 av den blå. Men sidan det er to av dei, blir det samla bidraget 1/4.
På same måten kan vi visa at det samla bidraget til dei fire gule trekantane er 1/4 av dei to grøne. Hvis vi no kallar arealet av den blå trekanten for T, så får vi no følgande uendelige sum å rekna ut for å finna arealet av parabelsegmentet (kalla Area i formelen):
Dette kan vi omskriva som:
Det kan sjå ut som at vi ikkje kjem lenger her: Vi kan jo ikkje faktisk utføra ein slik uendelig sum, for då blir vi jo aldri ferdige! Men vi kan likevel finna ut kva denne summen må bli. I dag kan vi enkelt rekna ut dette ved at vi kjenner igjen uttrykket inne i parentesen som ei uendelig geometrisk rekkje. Ei geometrisk rekkje er summen av ledd som er slik at kvart ledd er lik ein konstant k gonger det forrige. Det første leddet (som vi kallar a1) er 1, og det betyr at k = 1/4. Det tredje leddet må då vera lik det andre (1/4) gonger k (1/4) som blir 1/16. Når |k| er mindre enn 1, veit vi at denne rekkja konvergerer, dvs. nærmar seg ei grense. Og når vi kjenner formelen er det ikkje vanskelig å rekna ut:
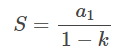
Vi set inn a1 = 1 og k = 1/4, og får S = 1/(1-1/4) = 4/3. Med andre ord arealet av parabelsegmentet er lik 4/3 * arealet av den blå trekanten.
No er vi egentlig ferdige, for vi har vi vist det vi skulle. Men vi har
"juksa" litt, for Arkimedes hadde ikkje denne formelen! Han var derimot
svært flink i Geometri, og fant det ut ved hjelp av følgande figur:
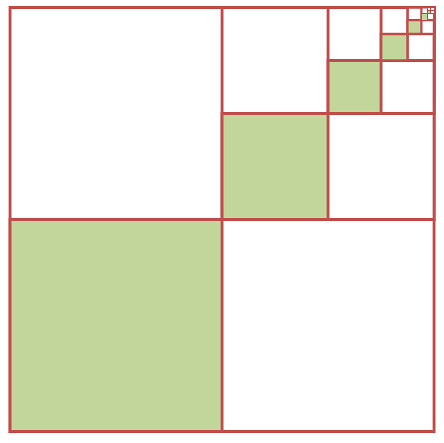
Her har vi først delt eit kvadrat med side lik 1 inn i fire like deler, så den første grøne firkanten har areal lik 1/4. Så har vi delt den øvre fjerdedelen til høgre i fire, og får då 1/16. Og slik kan ein forsetja. Det samla arealet av dei grøne felta er då lik den uendelige summen 1/4 + 1/16 + 1/64 ... Dette arealet må bli 1/3, fordi vi har to like areal, eller summar, på oversida og på undersida. Altså må disse summera seg til 1. På denne måten viste han at uttrykket inne i parentesen vart 1 + 1/3 = 4/3.
LENKER
Bevis for setningen på Proof Wiki.
