Pi à la Arkimedes
Talet pi blir også kalla Arkimedeskonstanten, og ikkje uten grunn, for rundt år 250 fKr. vart Arkimedes den første som rekna ut ein verdi i motsetning til å måla den. Og ikkje bare det: han fant også ein metode (algoritme) for å finna pi med så stor nøyaktighet vi treng. Vi skal gå i Arkimedes sine fotspor for å forstå litt om korleis han gjorde det. Sjølve metoden er slik som Arkimedes gjorde det i sin Measurement of a Circle (Gresk: Κύκλου μέτρησις, Kuklou metrēsis). Formlane og notasjonen er moderne, og føljer artikkelen Archimedes and Godfrey. Du kan gjerne også sjå den engelske oversettelsen av Measurement of a Circle, men den er litt tunglest.
Utgangspunktet
Arkimedes visste at omkretsen til ein sirkel måtte liggja mellom omkretsen til ein omskriven regulær mangekant, og ein innskriven regulær mangekant. Så han starta med ein regulær sekskant slik: (Den raude trekanten får vi straks bruk for)
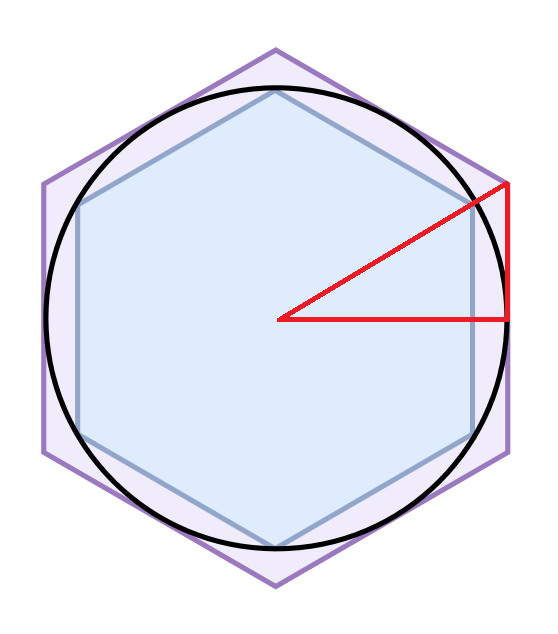
Arkimedes fant deretter ein metode som gjorde at kan kunne dobla antal sider og finna omkretsane av den nye omskrivne og den nye innskrivne mangekanten. På denne måten kunne han finna stadig betre verdiar for øvre og nedre grense for pi. Denne metoden kan i prinsippet gjentakast i det uendelige. Det einaste som begrensar oss er kor nøyaktig vi klarar å rekna. Sjøl klarte Arkimedes, eller kanskje vi heller skal sei offentliggjorde han, ei utrekning der han brukte ein regulær 96-kant, og fant dermed ut dette:
Forholdet mellom omkretsen og diameteren av ein sirkel er større enn 3 og 10/71 men mindre enn 3 og 1/7.
Lemma
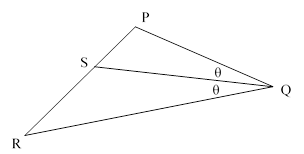
For å begynna trengte Arkimedes ein hjelpesetning, eller det som matematikarane kallar eit lemma. Dette var ein kjent hjelpesetning som fins hos Euklides (Proposition 3, Book VI of Euclid’s Elements) og er som følger: Gitt ein trekant PQR, og ei linje gjennom Q som halverer vinkelen PQR og treff den motståande sida i punktet S. Då gjeld at PS/SR = PQ/QR. Dette er illustrert i figuren under.
Beviset er ganske rett fram: Vi forlenger linja QS, og feller ned normalar frå R og P på den. Normalen frå R på denne linja treff i punktet U, og tilsvarande normal frå P treff i punktet T, som vist under:
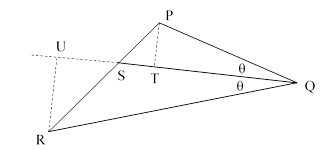
Sidan trekantane QTP og QUR er formlike, så har vi at PT/RU = PQ/RQ. Tilsvarande er trekantane RUS og PTS formlike, og det gir at PS/RS = PT/RU = PQ/RQ, som var det vi skulle visa.
Metoden
Figuren under illustrerer den metoden som Arkimedes brukte for å finna den øvre grensa for pi. Vi ser først på den raude trekanten frå den første figuren over. Grunnlinja er lik radien i sirkelen, og vi lar den vera 1. Kateten a0 er halve sida av den omskrivne sekskanten, og b0 er hypotenusen. Når vi halverer vinkelen får vi ein ny trekant med ei høyde som vi kallar a1 og ein hypotenus som vi kallar b1. Vi er no ute etter å finna ein regel som lar oss rekna ut disse nye verdiane.
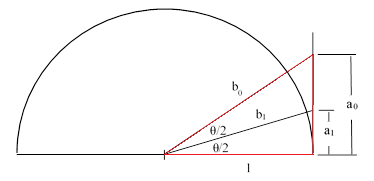
Arkimedes rekna bare med sider og forhold mellom sider. Spesielt var han opptatt av forholdet mellom radien og høyden, som vi skal kalla α, og forholdet mellom hypotenusen og høyden, som vi skal kalla β. Arkimedes sjøl navngav ikkje disse forholda, som vi har gjort her. Men så navnga jo han heller ikkje pi, men omtalte også den som eit forhold. Startverdiane til våre nye variablar er gitt som α0 = 1/a0 og β0 = b0/a0. Vi ynskjer no å finna ein formel for α1 = 1/a1 og β1 = b1/a1. Til dette kan vi bruka lemmaet vårt, som gir at b0 = (a0 – a1)/a1, og det gir oss at α1 = α0 + β0. Dessutan gir Pythagoras at 1 + a12 = b12, og når vi dividerer alle ledd med a12 får vi at α12 + 1 = β12. Då har vi altså funne formlane for α1 og β1.
Generalisering
Denne utrekninga kan vi no gjenta så mange gonger vi vil. Når vi byter ut indeksane 0 med j og 1 med j+1 (dvs. den neste), så får vi dei to rekursive formlane:
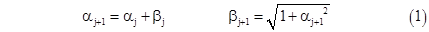
Dette virkar kanskje litt formålslaust. Men poenget er at når vi har brukt formelen mange nok gonger, og funne ein αn som vi er fornøyd med (eller ikkje orkar meir), så kan vi rekna oss fram til eit estimat for pi. Vi startar altså med ein mangekant med seks sider, og for kvart steg doblar vi antalet. Så antalet sider i steg n er lik 2n * 6. Sidan an er gitt ved an = 1/αn, og vi huskar at an er halve sida, så blir omkretsen O = 2 * 2n * 6 * 1/αn. Så når vi også huskar at diameteren = 2, så betyr det at formelen vår for pi blir :
Pn = 2n(6/αn)
Husk at det vi finn her er eit den øvre grensa for pi. Arkimedes
fortsette med å finna ein metode for å finna også den nedre grensa, og
slik kunne han snevra inn det mullige området for pi, skritt for skritt.
Men vi skal først bare rekna på den øvre grensa, fordi den konvergerer:
Jo større n blir, jo nærmare pi kjem vi.
Utrekning og program
For å komma i gang med utrekninga treng vi startverdiar. Trekanten vår har vinklane 30, 60 og 90 grader. Derfor er a0 lik halve b0. Ved å bruka Pytagoras finn vi då at a0 = 1/√3 og b0 = 2/√3, som gir oss følgande startverdiar: α0 = √3 and β0 = 2.
Sjøl med kalkulator er dette ein tung jobb å rekna vidare på. Men det er derimot ganske lett å laga eit program som reknar ut dette for oss. Så her er vår metode uttrykt i Python:
import math
# Startverdiar
alfa = math.sqrt(3)
beta = 2
# Reknar ut og skriv ut startverdiar for pi
print("n pi feil")
print("===============================================")
pi = 6 / alfa # 2**n blir 1, sidan n = 0
feil = math.pi - pi # Kor mykje vi bommar
print(0,"\t{:.16f}".format(pi),"\t",feil);
N = 4 # Så langt rekna Arkimedes
for n in range(1,N+1):
alfa = alfa + beta
beta = math.sqrt(1 + alfa*alfa)
pi = 2**n * 6 / alfa
feil = math.pi - pi
print(n,"\t{:.16f}".format(pi),"\t",feil) Utskrift
Når vi kjører dette slik det står, får vi denne utskriften:
n pi feil
===============================================
0 3.4641016151377548 -0.3225089615479617
1 3.2153903091734723 -0.07379765558367923
2 3.1596599420975005 -0.018067288507707335
3 3.1460862151314348 -0.004493561541641711
4 3.1427145996453683 -0.0011219460555751404
Hvis vi lar programmet rekna i N = 25 iterasjonar, blir den siste utskriften slik:
25 3.1415926535897940 -8.881784197001252e-16
Vi kan samanlikna dette med Python sin innebygde verdi i mattepakke. Hvis vi skriv math.pi i konsollet får vi ut: 3.141592653589793, så vi ser at vi har feil i den femtende desimalen etter kommaet. Hvis vi kjører programmet endå lenger, så vil vi sjå at det stoppar faktisk der. Dette er altså den mest nøyaktige pi vi klarer med akkurat denne versjonen av programmet. Men det er ikkje Arkimedes sin feil! Problemet er at her begynner beregningsfeil å komma inn. Dette har med korleis Python representerer tal i minnet på. Vanlige Pythonprogram representerer reelle tal som ein float, men vi kan gjera det betre hvis vi bruker decimal. Spørsmålet er korfor skulle vi det? JPL (NASA sitt Jet Propulsion Laboratory) bruker den same pi som Python gir oss i konsollet. Så det betyr at hvis du skal gjera utrekningar for rakettforsking, så er vår pi god nok!
No har vi altså funne den øvre grensa. Men kva med den nedre? Må vi gjennom alt dette pånytt? Nei, ta det ganske med ro. Det viser seg (dvs. dette har jo de godeste Arkimedes tenkt ut for oss) at vi kan vi bruka variabelen β i staden for α, og rekna ut den nedre grensa for pi. Korfor det blir slik, kan vi sjå hvis vi forandrar litt på tegningen vi brukte i stad:
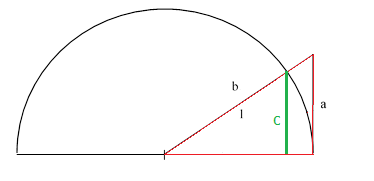
Vi huskar at β var lik forholdet b/a, altså hypotenus / katet i den raude trekanten. Men i den nye trekanten vi har laga med grøn katet (som vi kallar c), så er hypotenusen lik radien i sirkelen, altså 1. Men pågrunn av formlikhet må forholdet β fremdeles vera lik hypotenus / katet, dvs. 1/c. Snur vi denne likninga får vi at c = 1/β. Kateten c er lik den halve lengda av den innskrivne mangekanten, og tilsvarar altså a som var halve sida i den omskrivne. Det betyr at vi kan gjenbruka reknestykket vårt for pi, og få at
pn = 2n(6/βn)
Forskjellen er at no får vi altså eit nedre estimat, og derfor har vi brukt liten p istaden for stor P. Det dette kokar ned til er at vi kan erstatta alfa med beta i dei to linjene der vi reknar ut pi i programmet vårt. Gjer vi det, får vi dette resultatet:
n pi feil
===============================================
0 3.0000000000000000 0.14159265358979312
1 3.1058285412302489 0.03576411235954424
2 3.1326286132812382 0.00896404030855491
3 3.1393502030468672 0.0022424505429259334
4 3.1410319508905098 0.000560702699283322
Arkimedes si utrekning
La oss til slutt sjå kor langt Arkimedes kom. Han begynte altså med ein sekskant, og slutta med ein 96-kant. Det er fire doblingar, det vil sei så langt vi kjørte programmet i sin opprinnelige versjon. Men Arkimedes hadde ikkje ein nøyaktig måte å finna kvadratrøter på. Så han fant brøkar som gav god tilnærming. Og her er det han fant, ifølge artikkelen vår:
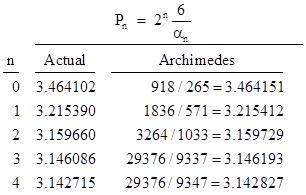
Den siste brøken er lik 3 + 1335/9347. Men hvis vi gjer nevnaren 2 mindre (dvs. får ein bittelitt større brøk), så kan vi forkorta: 1335/9345 = 1/7. Så no ser vi korleis Arkimedes fant den øvre grensa si som 3 og 1/7. Med desimaler blir det 3.142857142857143
Ser vi på utrekninga for den nedre grense, så fant han disse verdiane:

På same måten som over, har Arkimedes erstatta brøken 25344/8069 (= 3.1409096542322468) med noko som er litt mindre, men samtidig lettare å huska, nemlig 3 og 10/71 (= 3.140845070422535). Så dette tar Arkimedes som si nedre grense. Med andre ord:
3 og 10/71 < π < 3 og 1/7.
Det er forøvrig ikkje kjent korfor Arkimedes stoppa med ein 96-kant. Muligens har han rekna lenger, men meinte at dei gitte tala er meir praktiske, så han tenkte nok at dette fekk halda. (Og den stod seg jo i mange hundre år) Uansett: han hadde vist oss metoden, og då kan den som vil rekna ut betre verdiar, slik som vi har vist her.
LENKER
Approximations of π (Wikipedia)
