Bevegelsesmengde

Bevegelsesmengde (kallast på norsk også massefart, driv osv., og på engelsk bruker ein navnet momentum) er definert som masse * fart. Symbolet er som regel liten p (NB må ikkje forvekslast med trykk som ofte bruker samme bokstav) Altså er definisjonen:

p = m*v.

Enheten blir derfor kg * m/s. Sidan fart ein ein vektor, så er også bevegelsesmengde ein vektor. Bevegelsesmengde har samanheng med begrepet treghet og med treghetsloven, dvs. Newtons første lov. Historisk er bevelsesmengde beslekta med bregrepet impetus.

Bevaring av bevegelsesmengde

Både i verkeligheten og i simuleringar* og spill skjer det ofte kollisjonar (ofte kalla støt i fysikken) , og for at vi skal kunna modellera disse korrekt, må vi kjenna til fysikken som gjeld. Det viktigaste er bevaringsloven for bevegelsesmengde:

Bevegelsesmengde er bevart i kollisjonar der det ikkje virkar ytre krefter eller der summen av dei ytre kreftene er null. Det vil sei at samla bevegelsesmengde før kollisjonen er lik samla beveglsesmengde etter kollisjonen. Denne loven kan utledast frå Newtons tredje lov, og slik blir det som regel framstilt i lærebøkene. Men det er gode grunnar for å hevda at denne bevaringsloven er meir grunnleggjande enn N1. For den kan utledast frå antagelsen om at fysikkens lover er uavhengige av posisjonen. Les meir om dette i artikkelen om bevaringslover.

Kinetisk energi er derimot som regel ikkje bevart. Men når harde kuler, som feks biljardkuler kolliderer, kan vi rekna at den totale kinetiske energien er bevart. Slike kollisjonar kallast elastiske. Andre eksempel er når vi kastar ein sprettball mot golvet og den sprett opp igjen. Men dette er i teorien. I verkeligheten er slike makroskopiske kollisjonar alltid uelastiske, fordi ein (mindre eller større) del av energien går over til termisk energi. Hvis gjenstandane heng saman etter kollisjonen, så seier vi at den er fullstendig uelastisk. Dette kan feks. skje i bilkollisjonar. Det fins andre "kollisjonar" som egentlig ikkje er det fordi det ikkje er kontakt mellom gjenstandane, som er elastiske vekselvirkningar. Eksempel er Rutherford sitt eksperiment der ein alfapartikkel blir sendt mot gullfolie. Eit anna eksempel er den såkalte Gravity Assist eller slingshotmanøveren som gjer at eit romskip kan vinna fart ved å driva forbi ei planet. Men her skal det handla om vanlige kollisjonar.

Kollisjon i 1D (sentralt støt)

Eksempel 1: elastisk støt

Når ei kule treff ei anna kule rett på, og begge beveger seg langs den same rette linja, kallar vi dette eit sentralt støt. Vi skal sjå på eit enkelt eksempel med elastisk støt der den eine gjenstanden er i ro før støtet. Vi antar også at gjenstandane har same masse.

Vi set først opp den generelle likninga for bevaring av bevegelsesmengde i 1D. Hvis vi kallar massane m₁ og m₂, og fartane til disse før kollisjonen for hhv. u₁ og u₂, så er den samla bevegelsesmengda før kollisjonen m₁ u₁  + m₂ u₂. Tilsvarande blir summen etter kollisjonen m₁ v₁  + m₂ v₂. Her har vi altså kalla fartane etter støyten for v. Altså er den mest generelle formelen vi kan setja opp slik:

m₁ u₁  + m₂ u₂ = m₁ v₁  + m₂ v₂.

I vårt tilfelle er massane like, så vi kan sløyfa indeksane. Vidare er u₂ = 0, fordi den ligg i ro. Så likninga forenklar seg til:

m u₁  = m v₁  + m v₂. No kan vi korta vekk m-ane, og får det vi kan kalla likning I:

I: u₁  = v₁  + v₂.

Med andre ord: I vårt eksempel får vi at summen av fartane etter støyten er lik farten til kule 1 før støyten. Her har vi opplagt uendelig mange løysingar! For å komma vidare må vi derfor ha ein likning til, og då bruker vi den andre opplysningen vi hadde, som var at støyten var elastisk. Det vil sei at summen av dei kinetiske energiane før støyten er lik summen etter støyten. Generelt har vi altså at:

1/2 m₁ u₁² + 1/2 m₂ u₂² = 1/2 m₁ v₁² + 1/2 m₂ v₂². Vi kan alltid ta bort dei halve, og for vårt tilfelle kan vi vidare fjerna (forkorta) alle m-ane, sidan dei er like, samt u₂, sidan den var null. Då får vi det vi kan kalla likning II:

II: u₁²  = v₁² + v₂². No har vi to likningar med tre ukjente, og då skulle ein tru at vi fremdeles manglar ein! Men sjå kva som skjer nå vi set likning I inn i likning II:

(v₁  + v₂)² = v₁² + v₂². Dette er det same som:

v₁²  + 2 v₁ v₂ +  v₂² = v₁² + v₂². For at dette skal stemma må vi at at v₁ v₂ = 0! Med andre ord må minst ein av fartane etter støyten vera null. Vi kan ikkje ha at begge er null, for det vil bryta med prinsippet om bevaring av bevegelsesmengde. Og vi kan heller ikkje ha at v₁ er null, for då står jo ball 2 i veien. Så den einaste fysisk mulige løysinga er at v₂ = 0. Altså slik:

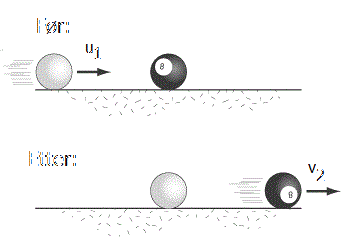
I dette tilfellet har altså kulene "bytta fart". Kule 2 fortset med den farten kule 1 hadde, og kule 1 blir ståande i ro. Og det viser seg at når massane er like, så vil alltid kule 1 og kule 2 bytta fart.

Variant 1: Hvis massane ikkje er like, så blir det litt annleis. Vi kan sjå litt på ein variant der  m₁ = 2m₂, altså at den innkommande kula er dobbelt så tung som den andre. La oss også setta at u₁ = 1m/s. Vi skal ikkje rekna på det, men svaret blir at v₁ = 1/3 m/s, og v₂ = 4/3 m/s. Dette stemmer sjølsagt ikkje med likning I, for det var jo forutsetnigen at begge massane var like. Men det stemmer med både bevaring av bevegelsesmengde og kinetisk energi. Sjekk sjøl! I denne varianten vil altså kule 1 fortsetja med redusert fart, mens kule 2 vil "susa" ut med høgare fart enn det kule 1 hadde.

Variant 2. Så kan vi også spørja ka som skjer hvis kule 1 er lettare enn den andre, feks m₁ = 1/2 m₂. Her blir svaret at v₁ = -1/3 , og v₂ = 2/3 m/s. Altså vil den lette kule 1 spretta litt tilbake (dvs. få negativ fart. Vi reknar her postitiv retning til høgre).

Variant 3: Kollisjon med vegg. Hvis kule 1 kolliderar med ein vegg, så kan vi rekna masse 2 som uendelig. Det som då skjer er at kule 1 vil få same fart, men motsett retta, altså spretta tilbake. Veggen vil rimeligvis fortsatt stå i ro!

Eksempel 2: Uelastisk støt

Hvis vi vender tilbake til kule-eksempelet med like massar, så hadde vi altså likning I: u₁  = v₁  + v₂,  som har uendelig mange løysingar. Men vi klarte å finna ein når vi hadde ein ekstra likning. Alle dei andre løysingane representerer variantar av uelastiske støyt, der vi taper kinetisk energi. Vi kan rekna på eit fullstendig uelastisk støyt, der kule 1 og kule 2 blir hengande saman. Vi kan tenkja oss at dei har eit slags klister på seg. Dette betyr at v₁  = v₂, dvs. u₁  = 2v₁. Altså fortset begge kulene med halve farten til kule 1.

Variantar: Dette var når massane er like. Hvis massane er ulike, så vil dei fortsetja med ein fart som er mindre enn u1. Hvis massen til kule 1 er større enn kule 2, så vil dei fortsetja med ein fart som er meir enn halvparten av den opprinnelige, mens hvis massen til kule 1 er mindre, så vil dei fortsejta med ein fart som er under halvparten.

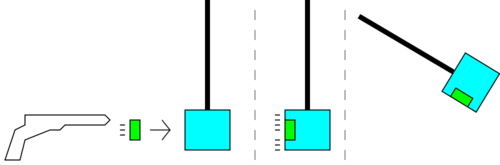
Ein versjon av dette siste eksempelet er mykje brukt som eksperiment i skulefysikken for å finna utgangshastigheten til eit prosjektil (ofte ei luftgeværkule). Sjå figuren under. Her heng det ein klosse eller klump med plastilin eller liknande. Poenget er at kula må bora seg inn i denne klumpen slik at den blir hengande fast. Klumpen heng i ro før støyten, men etterpå fortset kule og klump med same fart. Når klumpen er hengt opp som ein pendel, vil den gjera eit utsving til høgre, og vi kan då måla kor stort dette utsvinget er. Vha. bevaring av total mekanisk energi (vi ser altså bort frå luftmotstand) kan vi finna den kinetiske energien som kule+klump hadde rett etter støyten, fordi det vil tilsvara den potensielle energien dei har i ytterstilling.

Her er ein animasjon du kan leika deg med for å simulera kollisjonar i 1D. To gjenstandar kolliderer, og du kan variera massane og fartane til gjenstandane, og du kan endra elastisiteten. Hvis du set den til 1 får du ein elastisk kollisjon, og 0 vil då gi ein fullstendig uelastisk kollisjon.

Kollisjon i 2D (skrått støt)

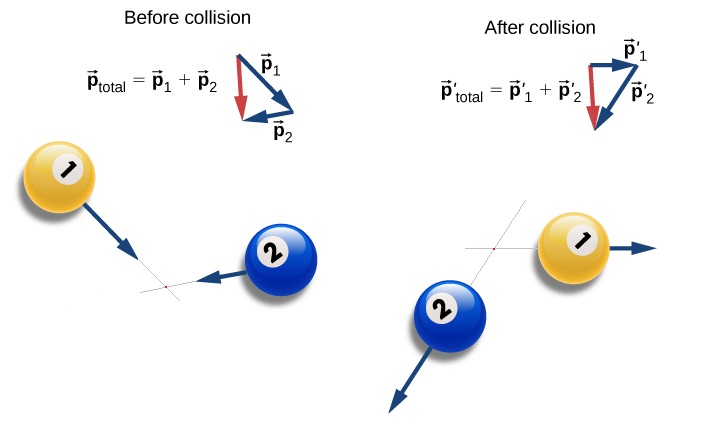
Vi vender tilbake til biljardkulene våre. Når kulene ikkje treff kvarandre rett på, så vil dei generelt ha ulike retningar, både før og etter støtet. Då får vi det som kallast skeivt (skjevt) støt. Då må vi bruka vektorrekning. Figuren under viser at før støtet har kule 1 bevegelsesmengda p₁, og kule 2  p₂. Begge disse er altså vektorar. Den totale bevegelsesmengda før støtet finn vi då som vektorsummen p_total =  p₁ +  p₂. Denne er vist som den raude pila til venstre. Etter støtet har kule 1 bevegelsesmengda p'₁, og kule 2  p'₂. Vektorsummen av disse to er p'_total = p'₁ +  p'₂. , og er vist som den raude pila til høgre. Som vi ser er disse to like: p_total = p'_total. 

For å rekna på dette treng vi å kjenna ikkje bare verdiane til fartsvektorane, men også retningane. Så det blir litt knotete rekning enn i det lineære tilfellet, men i prinsippet er det ganske likt som det vi har gjort over.

* Her kan du lesa meir om kollisjonar i simuleringar.

LENKER

Impulse, Momentum, and Collisions.

The Physics Of Billiards.