Vektorar

Ein vektor er en størrelse med både verdi og retning som feks. kraft, fart og akselerasjon. Vanlige tal uten retning kallar vi for skalare størrelsar. Eksempel på det er energi, temperatur og tid. Vi tegnar ein vektor som ei pil der pilspissen viser retningen og lengden av pila viser verdien. Merk at startpunktet for ein vektor ikkje har betydning. Det vil sei at vektorar med same lengde og retning er like. Vi kan altså parallellforskyva pilene våre uten at vi får ein ny vektor. Dette benytter vi oss av i addisjonen under. I lærebøkene er vektorar som regel skrivne som ein bokstav med pil over. Men her vil vi bruka utheva skrift for å skriva ein vektor. Verdien, eller lengden, av ein vektor v skriv vi som | v |. To vektorar som har same eller motsatt retning, men ulik verdi er parallelle. Ein vektor som har same lengde med motsatt retning til vektor a, kallar vi den motsatte vektoren -a.

Vektoraddisjon. Grafisk metode

Summen av to vektorar a og b kan vi finna på to måtar: 1) ved å la begge pilene starta i samme punkt og laga et parallellogram som vist i figuren. Vektorsummen r = a + b finn vi då som diagonalen i dette parallellogrammet. 2) ved å parallellforskyva vektor b slik at den startar der vektor a sluttar. Vektorsummen finn vi då frå starten av vektor a til slutten av vektor b. Eit greit eksempel på dette er forflytning. Hvis vi først går frå A til B, og deretter frå B til C, så har vi til saman flytta oss frå A til C.

Summen av a og den motsatte vektoren -a er lik nullvektoren 0. Denne har lengde lik null, og er definert til å vera parallell med alle vektorar.

Summen av tre eller fleire vektorar følgjer samme prinsippet ved å plassera vektorene etter kvarandre hale mot hode. Rekkefølgen har ingen betydning.

Eksempel 1: kraftsum

Vi tenkjer oss ein gjenstand liggande på eit friksjonslaust underlag, og at to stykker drar på objektet med kreftene A og B som virkar i ulik retning. Dette kan vi tegna slik (sett ovanfrå).

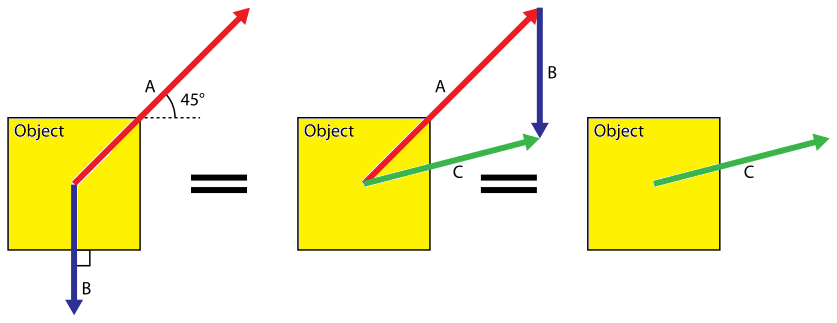
Vi finn først summen av dei to kreftene som vektorsummen C = A + B. Då veit vi at gjenstanden vil forflytta seg i retning langs C. Vi veit også at gjenstanden vil få ein akselerasjon i denne retningen. For å finna den kan vi bruka Newtons 2. lov og finna a som C/m der m er massen til gjenstanden. Ofte finn vi vektorsummen vha. koordinater. Sjå nedanfor.

Dekomponering

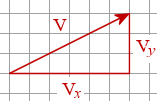
Ein vektor v kan skrivast som ein vektorsum av to vilkårlige vektorar a og b, så lenge disse ikkje er parallelle. Mao.:  slik at a + b = v. Dette kallast å dekomponera vektoren v, og a og b kallast komponentane. Det er (uendelig) mange måter å dekomponera ein vektor på. Det vanlige er å dekomponera ein vektor i ein komponent parallell med x-aksen og ein komponent parallell med y-aksen. Nedanfor har vi dekomponert vektoren v slik at v =  v_x + v_y. Då kan vi også skriv vektoren på koordinatform som v = [v_x , v_y]. Meir om dette nedanfor.

Eksempel 2: klosse på skråplan.

Her kan det vera lurt å dekomponera tyngdekrafta G, i ein komponent Gp som går parallelt med skråplanet og ein komponent Gn som er normalt på planet.

Eksempel 3: dekomponering av akselerasjonen

Akselerasjonen a er også ein vektor. Ofte er det nyttig å dekomponera den i ein komponent som er parallell med fartsvektoren og ein som er normal. Kvart punkt på kurven til ein partikkel kan vi tenkja oss er ein del av ein sirkelbane. Då vil normalkomponenten peika inn mot sentrum, dvs. langs radien i sirkelen, og vi kallar den a_r. Den andre komponenten vil peika i retning av tangenten i punktet, og vi kallar den a_t. Det betyr at a_r fortel om banens krumning i punktet. Hvis a_r = 0, vil banen vera rettlinja i punket.  a_t fortel om kor mykje banefarten endrar seg. Ein sirkelbevegelse med konstant banefart vil ha   a_t  = 0. Les meir om sirkelbevegelse.

Vektorsubtraksjon. Grafisk metode

Det er to måtar å finne differansen mellom to vektorar a og b på. Enten "spiss til spiss", eller ved å addera den motsatte vektoren av a dvs -a.  

Spiss til spiss:
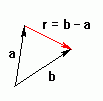
Vi lar vektorane starta i samme punkt. Vektordifferansen r = b - a vil då gå frå spissen av vektor a til spissen av vektor b. Merk rekkefølgen!

Addera den omvendte vektoren:
Vi snur vektoren a, og lar vektoren -a starte der b slutter. r vil da gå som normalt fra starten av vektor b til slutten av vektor -a. Vi ser at vi får den same vektoren som i stad.

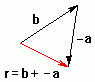
På samme måten som for vektoraddisjon, kan vi finna vektordifferansen vha. koordinatane til a og b:

Hvis feks. a = [1, 3] og b = [3,2], så kan vi finna differansen b - a som [3 - 1, 2 - 3] = [2, -1]

Eksempel 4: Differansen av to fartsvektorar

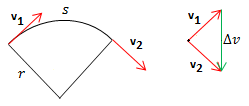
Denne figuren viser fartsvektorane v₁ og v₂ på to punkt i ein sirkelbevegelse. Til høgre har vi parallellforskyvd disse slik at dei startar i same punktet, og funne fartsendringen Δv =  v₂ - v₁ med "spiss til spiss"-metoden. Merk at denne peikar rett ned, dvs. inn mot sentrum av sirkelen. (Sjå sirkelbevegelse)

Produktet av ein vektor med ein skalar

Produktet av ein vektor m med eit tal k blir ein ny vektor med same (eller motsatt) retning som m, men med lengde lik k ganger den opprinnelige. I eksempelet under dannar vi ein ny vektor a = m + m + m = 3m. Her er k = 3, og a blir då ein vektor som har same retning som m, men som er 3 gonger lengre:

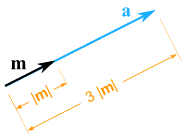
Hvis vi kan skriva ein vektor som eit tal multiplisert med ein annan vektor (a = k m), så er disse to vektorane (a og m) parallelle.

Skalarproduktet

Skalarproduktet eller prikkproduktet mellom to vektorar a og b er definert som lengden av a * lengden av b * cosinus til vinkelen mellom dei. Vinkelen mellom to vektorar er definert som den minste vinkelen mellom dei to linjene som går i forlengelsen av vektorane. På figuren er denne vinkelen kalla θ. Vi skriv skalarproduktet a · b, som då gir formelen:

a · b = |a| · |b| cos θ

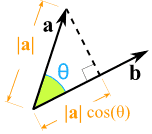
Når vinkelen er mindre enn 90 grader blir skalarpoduktet posistivt. Når vinkelen er større enn 90 grader, blir det negativt, og når vinkelen er akkurat 90 grader , blir skalarproduktet 0.

Eksempel 5: Arbeid

I fysikk kan Arbeid W uttrykkjast som skalarproduktet av krafta F og strekningen s, altså W = F · s. (sjå figur)

Vi bruker ei kraft på 5.83 N med ein vinkel på 31 grader og forflyttar ein klosse 12 m. Då blir arbeidet (avrunda):

W = 5.83N * 12m cos 31° = 60 J.

Kryssproduktet

Det fins også ein annan måte å multiplisera vektorar på, som heiter kryssproduktet som også er nyttig i fysikken.

Vektorkoordinater

Ein vektor i 2D, som startar i origo, og som ender  punktet (x,y), kan vi skrivast på koordinatform som a = [x,y]. Merk at vi då bruker klammeparentes.Vektorar i 3D skriv vi med tre koordinater: a = [x,y,z]

Vektoraddisjon og subtraksjon vha. koordinater
Hvis vektorane a og b begge er gitt på koordinatform, kan vi finna vektorsummen a + b  ved å summera x- og y-koordinatane kvar for seg. Hvis feks.
a = [2,1], og b = [1,2], så blir summen lik [3,3]. Altså: [1,2] + [2,1] = [1+2,2+1] = [3,3]

Tilsvarande er differansen a - b gitt som differansane mellom koordinatane: [1,2] - [2,1] = [1-2,2-1] = [-1,1]

Lengden av ein vektor v, kan vi finna med Pythagoras setning: | v | = (x² + y²)^1/2

Produktet av ein vektor med ein skalar finn vi ved å multiplisera inn talet i kvar koordinat: 3 * a = 3*[1,2] = [3*1, 3*2] = [3,6]

Skalarproduktet mellom a og b finn vi ved å multiplisera x-, og y-koordinatane og summera.

[1,2] ∙ [2,1] = 1*2 + 2*1 = 2 + 2 = 4.

Polarkoordinater

Hvis vi kjenner lengden av ein 2D-vektor r, og vinkelen mellom vektoren og x-aksen, så kan vi finna komponentane i  x- og y-retningen ved:

|r_x|= |r| cos θ.
|r_y| = |r| sin θ.

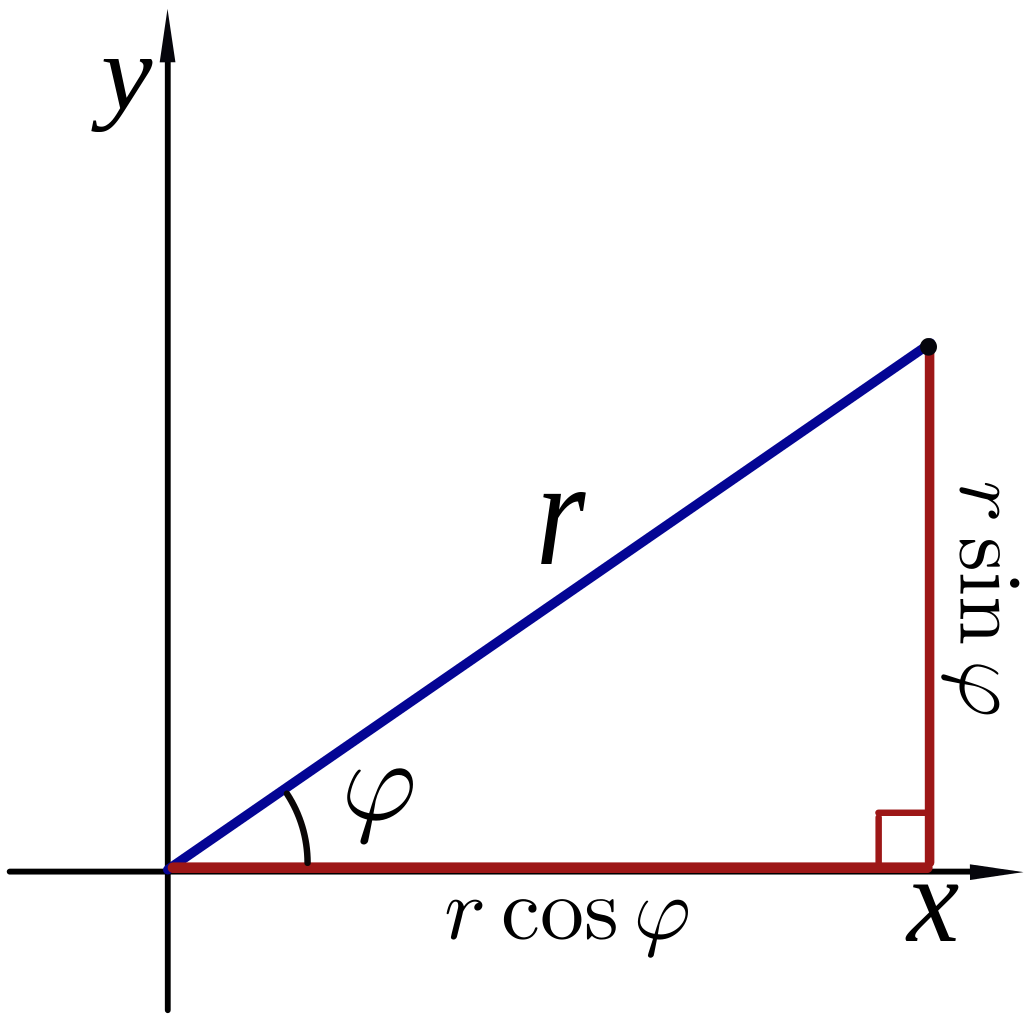
Dette betyr at vi kan bruka  θ og r som alternativ til koordinatane i x- og y-retning. Dette kallast polarkoordinater. For vektorar i 3D må vi i tillegg ha vinkelen mellom vektoren og z-aksen. Då får vi det som kallast kulekoordinater.

LENKER

Vektorer på NDLA