Utvalg i sannsynlighetsrekning
Vi tenkjer oss at vi skal plukka ut tilfeldig eit visst antal (k) ting frå ei mengde med i alt n ting, og så er spørsmålet: Kor mange forskjellige måtar kan vi kan gjera dette på?
Svaret på dette er avhengig av korleis reglane for å plukka ut disse tinga er. I LOTTO for eksempel, så kan vi ikkje leggja tilbake den kula vi har trukke ut. Dette kallar vi utvalg uten tilbakelegging. I LOTTO har heller ikkje rekkefølgen betydning. Hvis vinnar-rekkja er 2 7 17 19 22 26 33, så betyr det ingenting om 33-kula vart plukka ut først eller sist, eller innimellom. Det som tel er om du har dei riktige tala. Når rekkefølgen ikkje har betydning kallar vi det for eit uordna utvalg. Dermed kan vi dela inn i fire typer utvalg:
- Ordna utvalg med
tilbakelegging: PASSORD
- Ordna utvalg uten tilbakelegging: LOTTERI
- Uordna utvalg med tilbakelegging: PLUKK & MIKS
- Uordna utvalg uten tilbakelegging: LOTTO
Eksempel
1) PASSORD. Anta at du skal laga eit passord på k = 4 tegn, der kvart tegn skal vera ein engelsk bokstav. Hvis vi bare bruker små bokstaver, har vi dermed n = 26 tegn å velja blant. Vi får då 26 * 26 * 26 * 26 = 264 = 456976 ulike kombinasjonar. Dette er ein anvendelse av multiplikasjonsprinsippet. Her har rekkefølgen betydning: pp15 funkar ikkje hvis passordet er pp51! Men vi har lov til å ha like tegn. Det betyr at dette er ordna utvalg med tilbakelegging. Formel: nk
2a) LOTTERI La oss sei at vi sel n = 100 lodd og har k = 3 ulike
premier. Og i tillegg har vi ein regel om at ingen kan få meir enn ein
premie. Også her har rekkefølgen betydning fordi vi trekkjer førstepremien
først osv. Dette blir derfor ordna utvalg uten tilbakelegging.Når
vi trekkjer førstepremien har vi 100 mulige lodd. Men når vi trekkjer
andre har vi 99 igjen, og så til slutt 98. Alt i alt har vi då 100 *
99 * 98 = 970200 ulike måtar å trekkja ut dei tre vinnarane på. Formel:
n * (n-1) * .... *(n - k +1). Det siste leddet i vårt eksempel er
100 - 3 + 1 = 98. På kalkulatorar fins det ofte ein egen knapp for dette
som heiter nPr. I vårt tilfelle får vi 100P3 = 970200.
2b) Antall måtar å ordna n element. Kor mange kombinasjonar kan vi laga med tala 1 2 3 4 5? Dette kan vi sjå på som å trekkja 5 av 5 tal (ordna uten tilbakelegging). Etter samme tankegang som over, så har vi 5 muligheter for å trekkja første talet, 4 på det andre osv. Det gir oss totalt 5 * 4 * 3 * 2 * 1 = 120 muligheter. Dette talet kallast for 5 fakultet, og vi skriv det som 5! Vi kan altså ordna n ulike element på n! måtar. Dette er, som sagt, det samme som å trekkja 5 av 5, så vi skal få same tal om vi bruker nPr-knappen med 5 på begge sider: 5P5 = 120. Sjå eksempel på dette.
3) PLUKK & MIKS. Når vi plukker godteri av diverse typar i ein pose, så er det opplagt at rekkefølgen ikkje har betydning. Det er kor mange av dei ulike sortane vi plukker som har betydning. Vi har derfpr eit uordna utvalg. Og sjøl om vi ikkje legg tilbake, så kan vi i posen vår ha mange like bitar. Så når vi ikkje bryr oss om dei ulike bitane, bare om sorten, så kan vi sei at vi har eit uordna utvalg med tilbakelegging. Det kan ein sjølsagt også rekna på, og det fins ein formel. Men dei fleste lærebøker tar ikkje det med.
4) LOTTO. I trekningen på laurdagslotto plukker dei ut k = 7
kuler av totalt n = 34. For kvar gong blir kula lagt til side, så
dette er opplagt uten tilbakelegging. Lotto går ut på å tippa dei rette
tala, så her har rekkefølgen ingen betydning. Derfor er dette uordna
utvalg uten tilbakelegging. Men la oss likevel først rekna ut kor
mange utvalg det hadde blitt hvis rekkefølgen hadde hatt betydning. Då
ville dette blitt tilsvarande eksempel 2a over, så vi hadde fått 34 *
33 * 32 * 31 * 30 * 29 * 28 ulike utvalg. (34P7) Men dette talet er
alt for stort fordi det er veldig mange av disse som egentlig er samme
tala, bare ulik rekkefølge. Som vi såg i eksempel 2b, så kan vi ordna 7
tal på 7! måtar. Det betyr for kvart av dei setta som lottomaskinen
plukkar ut, så fins det tilsamen 7! = 5040 måtar å trekkja ut dei
same tala på. Det totale antal forskjellige sett er då gitt ved 34 *
33 * 32 * 31 * 30 * 29 * 28 / 7! = 5379616. Formelen er altså n
* (n-1) * .... *(n - k +1) / n! Dette kallast for
binomialkoeffisienten som ofte skrivest 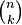 . Tilsvarande knapp på kalkulatorar er nCr.
I vårt eksempel får vi 34C7 = 5379616. Sjekk dette på
kalkulatoren.
Du kan også gjerne lesa meir
om Pascals trekant og binomiske forsøk.
. Tilsvarande knapp på kalkulatorar er nCr.
I vårt eksempel får vi 34C7 = 5379616. Sjekk dette på
kalkulatoren.
Du kan også gjerne lesa meir
om Pascals trekant og binomiske forsøk.
Oppsummering
La oss sjå på antall måtar å plukka to tall frå mengden {1, 2, 3, 4}. Her
er altså k = 2 og n = 4.
Dei to første kolonnene er ordna utvalg, dei to siste er uordna. Så er
disse igjen delt opp i med og uten tilbakelegging. Med så liten mengde å
plukka frå kan vi ramsa opp alle utvalg av dei ulike typane:
| Ordna | Uordna* | ||
| Med | Uten | Med | Uten |
| 11 | 11 | ||
| 12 | 12 | 12 | 12 |
| 13 | 13 | 13 | 13 |
| 14 | 14 | 14 | 14 |
| 21 | 21 | ||
| 22 | 22 | ||
| 23 | 23 | 23 | 23 |
| 24 | 24 | 24 | 24 |
| 31 | 31 | ||
| 32 | 32 | ||
| 33 | 33 | ||
| 34 | 34 | 34 | 34 |
| 41 | 41 | ||
| 42 | 42 | ||
| 43 | 43 | ||
| 44 | 44 | ||
| n2 = 16 | nPk = 12 | 10# | nCk = 6 |
*Dei uordna utvalga er sortert i stigande rekkefølge (slik som i LOTTO).
Det betyr at td. 31 ikkje står i lista fordi 13 allerede er med lenger
oppe.
# For dei som lurer er formelen (n+k-1)Ck. Her blir det 5C2 = 10.
Les meir om dei tre typane utvalg som er med i pensum på NDLA.
