Pascals trekant og binomiske forsøk

Pascals trekant er ein trekant med tall som følger eit bestemt mønster. Dette kan du sjå i det animerte bildet under. Her har vi laga ein struktur med celler som vi skal fylla ut.
Regelen for å finna tal er todelt: 1) Det skal vera 1 frå toppen og nedover langs begge kantane. 2) Dei andre tala finn vi som summen dei to tala som er i cellene direkte over.

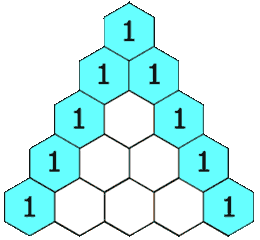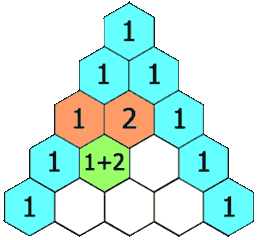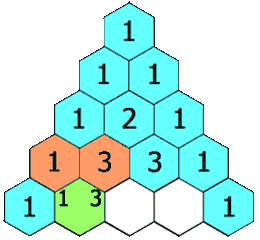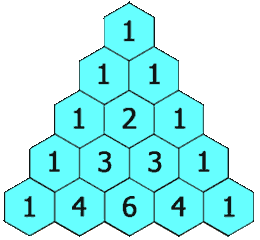
Her ser du trekanten fylt ut med litt fleire rader i henhold til regelen vår:

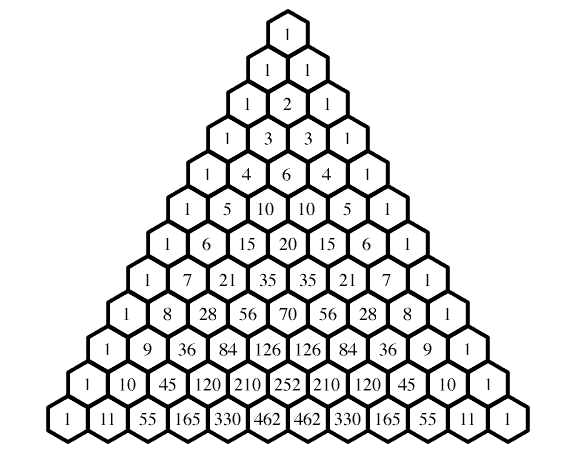
Binomialkoeffisientar

Det viser seg at kvart tal i Pascas trekant er lik den tilsvarande binomialkoeffisienten. Binomialkoeffisienten er definert ved formelen

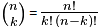
Vi kan tolka denne binomialkoeffisienten kombinatorisk som antalet måter å trekkja k ting av n mulige når vi trekkjer uten tilbakelegging og når rekkefølgen ikkje har betydning. (dvs. dette er uordna utvalg). Meir om dette under. For å få binomialkoeffisientane på rett plass i Pascals trekant lar vi n står for radnummer og startar med rad 0 på toppen, og for kvar rad lar vi k telja frå 0 til n mot høgre. Då får vi følgande mønster:

Du kan (og bør) sjøl sjekka at dette stemmer for dei første radene ved å enten bruka definisjonen over, eller du kan bruka "nCr"-knappen på kalkulatorar som har det, eller også funksjonen "nCr[]" i GeoGebra. Hvis gjer så er du gjerne alt no overbevist om at det stemmer for alle. Men å vera sikker på at det stemmer er ikkje det same som at det er bevist. Så la oss sjå på eit litt forenkla bevis:

Eit kombinatorisk bevis

Det vi treng å gjera er å visa at vi kan bruka akkurat samme regel for utrekning av binomialkoeffisientane som for Pascals trekant. Først legg vi merke til at alle binomialkoeffisienter med 0 under blir lik 1, altså 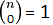. Og alle binomialkoeffisientar med same tal over og under blir også lik 1, dvs. 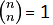. Dette betyr at tala langs begge kantane blir lik 1. Dermed har vi vist at del 1 av regelen vår er oppfylt. For å visa del 2 av regelen skal vi sjå på følgande eksempel:

Eksempel: Anta at vi har ein boks med fem kuler som vi kallar a, b, c, d, e. Så skal vi trekkja 3 av disse uten tilbakelegging. Når rekkefølgen ikkje betyr noko kan vi gjera det på 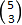 = 10 måter. Dette er så få at vi kan skriva alle opp: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde. Når vi no deler disse opp i utvalg med og uten a, så ser vi at det blir 6 + 4. Studerer vi no dei seks første, og bare ser på dei to siste bokstavane: (bc, bd, be, cd, ce, de) så ser vi at dette er det samme utvalget vi får når vi plukker  2 kuler av dei 4 som er igjen når a-en er lagt til side, altså 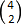. Dei fire siste svarar til å plukka 3 av dei 4 gjenverande kulene, altså .

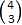Altså har vi vist følgande:


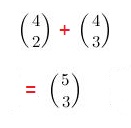
Og her har vi plassert koeffisientane riktig i forhold til kvarandre slik dei er i Pascals trekant. Men stemmer det for alle andre koeffisientar? Ja, for vi kan bruka det same resonnementet på alle utvalg. Hvis vi skal plukka k av n så kan vi gjera det på 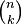måtar. Dette kan vi dela opp i dei med a, som er det samme som å plukka k-1 av n-1, og dei uten a som er det samme som å plukka k av n-1. Dette betyr at 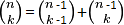 .  Dermed har vi vist (på ein litt forenkla måte) at  del 2 av regelen også gjeld.
Nedanfor skal vi sjå at vi får akkurat den same formelen når vi ser på antalet stiar til ei bestemt celle:

Antall stiar til ei celle

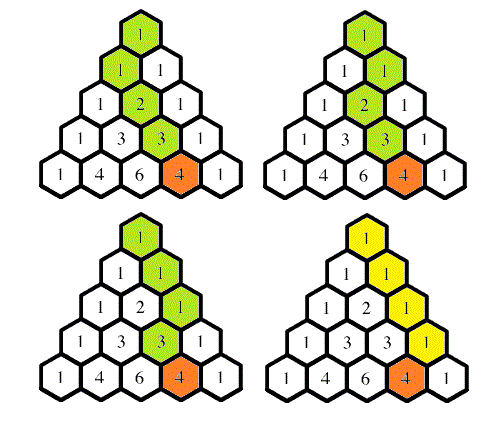
La oss no sjå på mulige stiar frå toppen og ned til ei bestemt celle. Kravet til ein sti er at vi for kvart steg bare går ned, enten til høgre eller venstre. Det er ikkje vanskelig å sjå at antall mulige stiar frå toppen og ned til ei bestemt celle er nettopp talet i denne cella. I eksempelet under fokuserer vi på den oransje cella som har verdien 4. Figuren viser dei fire mulige stiane til denne cella. Dei tre grøne stiane går via talet 3 i cella over til venstre. Den gule stien endar opp i cella over til høgre som har verdien 1. Summerer vi disse to får vi 1+3 = 4. Regelen for å finna antal stiar til ei vilkårlig celle er altså summen av antallet stiar til dei to cellene over. Det skulle forresten bare mangla, sidan disse det er bare gjennom dei to cellene over at vi kan komma til ei celle. Og igjen: sidan dette nettopp er den regelen som Pascals trekant er definert ved, så må resten av tala også stemma.

Tilfeldig vandring

No skal vi ta ein tur på Pascals trekant. Vi startar på toppen og går eit steg ned for kvar gong. Og så lar vi kronismen bestemma om vi skal til høgre eller venstre. Med andre ord vi kastar mynt og kron, og går til høgre hvis vi får mynt, og venstre om vi får kron. Kva blir då sannsynligheten for å havna i den oransje cella? For å finna ut dette ser vi først på ei delproblem, nemlig sannsynligheten for å havne i den oransje cella via den gule stien. Å gå den stien betyr at vi går tre gonger til høgre og ein gong til venstre. Produktregelen* seier då at sannsynligheten P(HHHV) = P(H) * P(H) * P(H) * P(V). Her er dette enkelt å rekna ut sidan kvar av disse er 0,5. Altså har vi at P(HHHV) = 0,5⁴. For dei tre grøne stiane fører samme resonnement til samme svar. No kan vi finna den totale sannsynligheten for å havna i den oransje cella som summen av disse, altså 4 * 0,5⁴ = 0,25.

No vil vi forandra på forsøket vårt litegrann. I staden for å kasta mynt og kron så trillar vi terning, og så bestemmer vi at vi går til høgre om den viser 1 eller 2, og til venstre. Sannsynligheten for å gå til høgre, som vi kan kalla p, er då p = 2/6 = 1/3. Og sannsynligheten for å gå til venstre blir 1 - p = 2/3. No kan vi finna sannsynligheten for å gå heile den gule stien. Den blir 1/3 * 1/3 * 1/3 * 2/3 = 2/27. Men igjen er det slik at vi får den samme sannsynligheten for å gå kvar av dei grøne stiane, fordi uansett kva rute vi tar til den oransje cella, så må vi til saman gå tre gonger til høgre og ein til venstre - det er bare at rekkefølgen er ulik. Vi kan derfor skriva opp sannsynligheten for å havna i mål er lik 4*(1/3)³*(2/3) = 0.1 (avrunda)

Binomiske forsøk

No skal vi generalisera dette resultatet og finna ein formel. Forsøka over er eksempel på det som kallast eit binomisk forsøk. Eit binomisk forsøk er når vi gjentar samme forsøk fleire gonger og ser på kor mange gonger ein bestemt hendelse A - som det å få 1 eller 2 på terningen - inntreff.  Vi innfører ein variabel X som antalet gonger A intreff. Det er eit poeng at sannsynligheten for at dette skal skje (som vi altså kalla p) er den same for kvart delforsøk. Når vi kastar mynt og kron er sannsynlighetene for å få mynt på andre kastet er uavhengig av om vi fekk mynt eller kron på første. Derfor kallar vi dette for uavhengige hendelsar. Vi kan tenkja oss at vi stiller oss på toppen, og for kvart delforsøk går vi ned til høgre hvis A inntreff, og til venstre hvis ikkje. For å havna i den oransje cella måtte vi gå tre gonger til høgre og ein til venstre. Dette svarer til at hendelsen A har skjedd 3 gonger, dvs. at X = 3. Med symbol kan vi skriva at sannsynlighetene for å gå ein bestemt delsti blir p³(1-p). Den totale sannsynligheten blir då p(X = 3) = 4*p³(1-p). Når vi husker på at firetalet kom frå binomialkoeffisienten 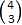, så kan vi no til slutt skriva opp sannsynligheten for at vi A skal inntreffa k av n gonger:



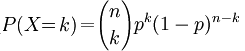
Og no treng vi egentlig heller ikkje Pascals trekant lenger, for den er bare eit hjelpemiddel for tanken. Formlane gjeld like fullt, sjøl om vi står i ro og kastar terningen!

Binomialteoremet

Til slutt skal vi sjå på noko anna, men som likevel heng nøye saman med det vi har sett på over. Når vi ganger ut såkalte binomer av formen (a+b)ⁿ så viser det seg at vi igjen finn tala frå Pascals trekant, vist i rødt under:

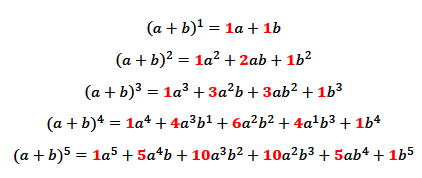
Og her bør du også prøva dette sjøl! Vi legg først merke til at kvar rad er alle ledda potenser av a og b, og med eit tal framfor. Ser vi på den nederste raden ser vi at den startar til venstre med a⁵ b⁰. (Husk at b⁰ = 1, så den skriv vi ikkje) Så kjem a⁴ b¹. (bare at vi skriv heller b i staden for b¹) Mønsteret her er at eksponenten til a minkar frå venstre mot høgre, mens eksponenten til b aukar. Når vi tenkjer på at (a+b)⁵ = (a+b)(a+b)(a+b)(a+b)(a+b), så kan vi også her tenkja kombinatorisk for å forstå korfor vi finn igjen binomialkoeffisientane når vi ganger dette ut. For når vi multipliserer disse fem parentesane med to ledd i kvar, så får vi egentlig 2⁵ = 32 antal ledd. Men mange av disse kan vi slå saman, nemlig dei med same koeffisentar for a og b. Vi har bare eit ledd med a⁵, fordi det er bare når vi multipliserer alle fem a-ane i alle parentesane at vi får a⁵. Men a⁴ kan vi få på fem måtar, nemlig ved å multiplisera fire a-ar med ein b, som enten kan komme frå parentes 1, 2, 3, 4 eller 5. Derfor får vi koeffisienten 5 framfor leddet a⁴ b. Vi veljer altså ein b av fem mulige, og det er 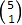måtar å gjera det på. 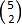Den neste koeffisienten blir som er lik 10, og det svarer til antalet måtar å trekkja 2 b-ar av 5. Vi kan altså skriva den nederste raden slik:



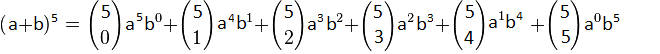
Før vi går vidare legg vi merke til at summen av alle disse koeffisientane blir 1 + 5 + 10 + 10 + 5 + 1 = 32 = 2⁵. Men dette visste vi jo at det måtte bli, sidan vi jo bare har gruppert saman dei 32 ledda vi starta med i henhold til eksponentane til a og b.

Generelt kan vi skriva:



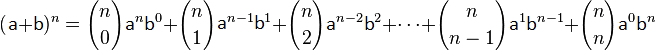
Dette kallast for binomialteoremet. Om vi bruker sumnotasjon kan vi skriva dette meir kompakt:


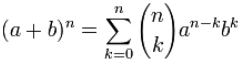
Det fins mange andre mønster i Pascals trekant, som td. Fibonacci-følgen mm. Men det får vi sjå på ein annan gong.

* egentlig er dette betinga sannsynligheter, men sidan vi har same sannsynlighet for å gå til høgre eller venstre for kvar gong, så kan vi skriva det på denne måten.