Trykk

Trykk blir definert som kraft per areal, når denne krafta F står normalt på flata. Vi bruker som regel bokstaven liten p for trykk, men det er heller ikkje uvanlig å finna stor P. Altså har vi at:

p = F/A

enheten for trykk er pascal (Pa) som er det samme som Newton per kvadratmeter. Altså Pa = N/m². Andre enheter er feks ein atmosfære som vi skal forklara nedanfor.

Trykk er ein skalar størrelse, dvs. det har ingen retning.

Eksempel

Vi tenkjer oss ein klosse som veg 100 N, og som har ei side på 0.1 m², og ei anna på 0.01 m². D viål trykket som oppstår på underlaget vera avhengig av kva side som vender ned. Med den største sida ned blir trykket p = 100 N / 0.1m² = 1000 Pa. I det andre tilfellet før vi at p = 100 N / 0.01 m² = 10 000 Pa.

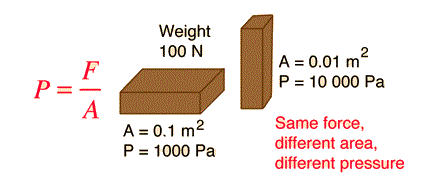
Så trykket aukar altså når arealet minkar. Eksempel på dette er knivar og nåler. Ein kniv kan skjerast med og ei nl kan stikkast med fordi dei har veldig lite areal på eggen / i spissen. Dei er spisse!

Lufttrykket

Lufttrykket oppstår fordi vekta av lufta i atmosfæren trykkjer ned. Vi kan tenkja oss ei søyle med luft som strekkjer seg frå bakken og opp til toppen av atmosfæren. Hvis denne søyla har grunnflate lik ein meter så blir lufttrykket ganske enkelt lik tyngden. Sidan luftsøyla blir lavare jo høgare opp vi befinn oss, så blir også luftrykket også lavare. Det viser seg at trykket ved havoverflata er rundt p₀ = 101 325 Pa, og dette er lik ein atm (atmosfære). På toppen av Mount Everest er det bare 1/3 så stort.

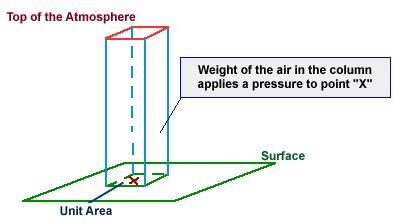
Trykket virkar i alle retningar.

Vi kan rekna ut krafta som virkar på eit bord på grunn av lufttrykket ved å snu på definisjonen. Då får vi at F = p * A. Eit bord med overflateareal på 1.5 m² som befinn seg ved havoverflata vil dermed bli utsatt for ei kraft lik F = 101 325 Pa * 1.5 m² = 152 kN (avrunda). Det er like mykje som om fire asiatiske elefantar sto på det! S korfor bryt ikkje bordplata i stykker? Svaret er at det virkar ei like stor kraft frå undersida av bordet, men den virkar oppover, slik at kreftene kansellerer kvarandre. Av samme grunn vil ikkje kroppen vår kollapsa på grunna av trykket, for vi har det same trykket inne i lungene.

Sugerøyr og sugekopp

Effekten av luftrrykket kan vi sjå i mange situasjonar frå kvardagslivet. Eit eksempel er sugerøyret. Når du drikk gjennom eit sugerøyr kjennest det ut som at du drar drikken oppover røyret. Men det som i verkeligheten skjer, er at du skaper eit undertrykk i munnen i forhold til nede i glaset. Denne trykkforskjellen skaper ein kraftforskjell soom er stor nok til at drikken blir pressa opp.

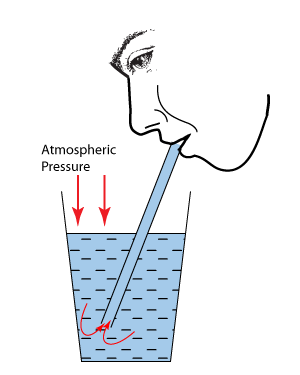
Dette fortel oss at det er ingenting som heiter sugekraft. Det er lufttrykket som pressar oppover. Tilsvarande er det lufttrykket som pressar ein sugekopp inn til den flata som den er festa på. Når vi presser sugekoppen mot flata vil vi pressa ut nesten all lufta. Dette skaper eit rom inne i sugekoppen med veldig lavt trykk. Men på utsida er det jo normalt lufttrykk. Så utanfor virkar det store krefter mot sugekoppen, mens inni er det veldig små.

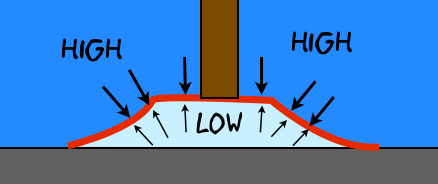
Betyr det at ein sugekopp ikkje vil henga fast i vakuum? Ja, nettopp! Sjå video her.

Barometeret

Den italienske fysikaren Evangelista Torricelli fant i 1643 opp eit apparat for å måla lufttrykket som i prinsippet er veldig likt eit sugerøyr. Dette er det første barometeret. Det besto i all sin enkelhet av eit meterlangt røyr som var stengt i botnen, og vart fylt med kvikksølv. Når han snudde dette oppned med opningen ned i eit kar med kvikksølv, så seig kvikksølvet litt ned og etterlot seg vakuum i toppen. Og vi huskar at det betyr at det ikkje virkar krefter nedover på kvikkølvsøyla. Høyden på søyla var då omtrent 760 mm. (korfor det?) Kvikksølvhøyden i mm var då den første enheten for trykk, og vi  ser at 1 atm = 760 mmHg.

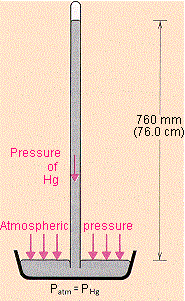
Det var sjølvaste Galielo som foreslo for Torricelli å bruka kvikksølv. Og grunnen var at kvikksølv var den tyngste væska som var tilgjengelig. Det er mulig å laga eit liknande vannbasert barometer, men i såfall blir røyret nesten ti meter høgt.

Hydraulisk jekk

Eit anna praktisk eksempel er ein hydraulisk jekk eller kraftforsterkar som vist under. Enkelt sagt består den av to stempel som virkar ned på ei hydraulisk væske, som vanligvis er ein slags olje. Disse to stempela går i sylinderar med ulike tverrsnitt. Til venstre pressar vi ned med ei kraft F₁ ned på stempel 1 med areal A₁, og på den andre sida trykkjer "lasta" (det vi skal løfta) ned med ei kraft F₂ på stempel 2 med areal A₂. Poenget no er at sidan stempela er forbunde med kvarandre gjennom eit røyr (og dei ligg i same høgde) så vil trykket på begge vera like. Då kan vi setja opp likningen p = F₁ / A₁ = F₂ / A₂. Dette gir at F₁ = F₂ * A₁ / A₂. Så hvis feks arealet A₁ er 100 gonger så stort, så betyr det at F₁ = 100 * F₂. Altså blir krafta vår hundredobla, og det er derfor vi kallar dette kraftforsterkar. Ein hydraulisk brems kan virka på same måte.

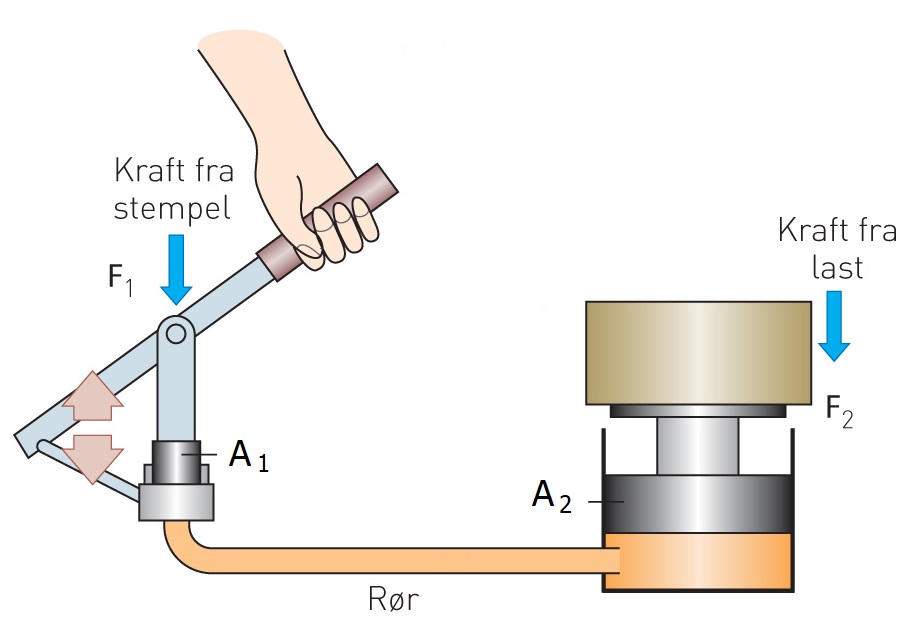
Pascals lov:

No skal vi fram til ein lov som Blaise Pascal kom fram til i 1653. Med ord, slik den blir fortalt på mange webstader, er den heller uforståelig. Men på matematisk form er den ganske enkel. Loven gir oss trykket som funksjon av dybden. Forutsetningen er at vatnet eller veska er inkompressibel. Med andre ord: er massetettheten ρ til væska er uendra ved ulike dybder. Det betyr at vi kan rekna ut massen i ei tenkt vannsøyle som ρ * V, og sidan Volumet er lik A * h, så har vi at m = ρ A h, og tyngden dermed lik ρ A h g. Den totale krafta som held oppe den tenkte vannsøyla må tilsvara tyngden av vatnet pluss tyngden av lufta over, og som vi har sett over er den lik trykket ganger arealet, altså p0 A. Då har vi formelen vi treng, nemlig p = p₀ + ρgh

No forstår vi at p(h) er ein lineær funksjon med stigningstal lik ρg. Derfor finn vi også denne loven på formen Δp = ρgΔh. Denne formelen kan vi feks. bruka til å rekna ut oppdriften av ein gjenstand som er nedsenka i væske. I vatn er ρg omtrent lik 1000 kg/m³ 10m/s² = 10 000 Pa/m. Då ser vi at når vi går 10m ned i vatnet så aukar trykket med 100 000 Pa, dvs. 1 atm. Så tommelfingerregelen er altså at trykket aukar med omtrent ein atmosfære for kvar tiande meter. Og der fekk vi også svaret (sant?) på korfor vi treng eit ti meter lang røyr for å laga eit vannbarometer.

Trykk i væsker og gassar.

Vi starta med å rekna på trykk frå ein klosse, dvs. ein fast gjenstand. Men ein gass er jo ikkje ein fast gjenstand. Likevel virkar gassen i ein beholdar med ei kraft på veggene. Korleis kan det ha seg? Svaret finn vi på mikroskopisk nivå. Gassen består av fryktelig mange molekyler (eller atomer). Disse suser fram og tilbake, og kolliderer med kvarandre, og mange kolliderer med veggene. Kvar kollisjon mellom vegg og molekyl vare bare eit lite øyeblikk og bidrar med svært lite kraft. Men sidan antalet molekyler er så stort, blir summen av alle disse kollisjonane betydelig. No forstår vi korfor trykket ikkje har ei retning. For alle disse kollisjonane skjer jo i alle mulige retningar:

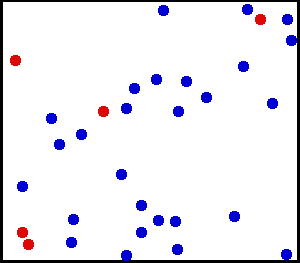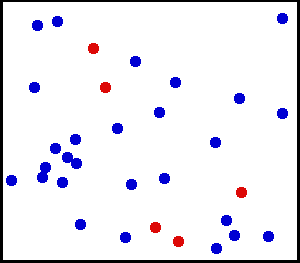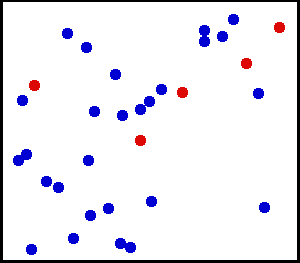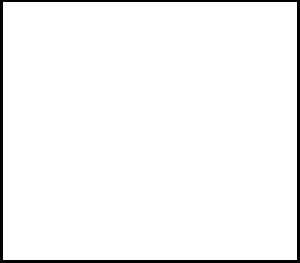
Eit molekyl i ein gass har ikkje den same farten som dei andre, og den har heller ikkje same farten heile tida. Men gjennomsnittsfarten har samanheng med temperaturen i gassen. Jo høgare temperatur, jo større fart har molekylane, og dermed blir krafta dei virkar med på veggen også større. Då blir vi ikkje så overraska når vi høyrer at trykket i ein gass aukar proporsjonal med temperaturen.  Trykket har også samanheng med volumet av gassen. Hvis vi har stengt inne ei bestemt mengde gass, dvs. ei bestemt mengde gassmolekyler i ein beholdar, så vil molekylane kollidera med veggene dobbelt så ofte hvis vi halverer volumet. Så trykket er altså omvendt proposjonalt med volumet. Dette kan du lesa meir om i artikkelen om gasslovene.