Snorkrefter

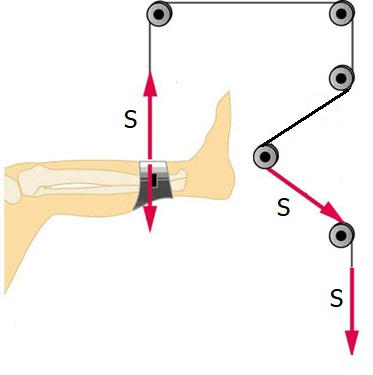
Mange fysikkoppgaver handlar om fleire gjenstandar som er bundne saman med snorer. Og alle disse oppgavene forutset då at snorene er masselause og at trinsene er uten masse og utan friksjon. For det er bare då at begrepet snorkraft gir meining. Hvis disse betingelsane er oppfylte, vil eit tau overføra krafta uforminska frå ein ende til ein annan. Hvis vi i figuren under drar nedover med ei kraft S på 100 N i enden av tauet, så vil det også virka ei kraft på 100 N oppover på foten i bildet. (NB: vi forutset at alle disse trinsene er festa på ein eller annan måte)

snorkraft

Korfor blir det slik?

Hvis du bare skal løysa oppgavene, så er gjerne ovenståande nok å vita. Men så lurer du kanskje på korfor det blir slik. Så la oss sjå litt på det. For det første er det feil å forklara det med Newtons tredje lov slik ein artikkel på naturfag.no gjer. Vi er nødt til å bruka Newtons andre lov.

Ein litt forenkla måte å forstå det på er å sei at hvis det virkar ein kraftsum forskjellig frå null på eit masselaust tau, så vil det føra til ein uendelig akselerasjon, sidan a = F/m, og m er 0. Ein slik situasjon er fysisk umulig, og derfor kan ikkje eit masselaust tau vera utsatt for ein kraftsum ulik 0. Det betyr at kreftene på tauet er like, men motsatt retta.

Eit verkeleg tau

I verkeligheten er jo ikkje tau masselause, men dei har som regel veldig liten masse i forhold til dei andre gjenstandane som er involvert. Så la oss no rekna litt på eit meir realistisk tilfelle. Vi drar i ei snor med krafta F1 = 11N. Snora har massen 0.1 kg. Snora drar så på ein klosse med krafta F2. Klossen har massen 1 kg. Her må vi først tenkja at klossen og snora er eit system med samla masse 1.1 kg, og den einaste ytre krafta er F1. Så Newtons andre lov på dette systemet gir ein akselerasjon på 11 N / 1.1 kg = 10 m/s2. No kan vi bruka Newtons andre på bare klossen, og då finn vi at F2 = 1 kg * 10 m/s2 = 10 N.

snorkraft

Som vi ser, i verkeligheten er F1 forskjellig frå F2. Men poenget no er at hvis vi tenkjer oss at massen til tauet blir mindre, så vil vi finna at disse to kreftene blir likare og likare. Og då kan vi kalla det for same krafta, sjøl om det i verkeligheten er to forskjellige krefter som er tilnærma like.
Ellers er det kanskje verd å merkja seg at F1 og F2 sjølsagt ikkje er motkrefter. Motkrafta til F1 er F1* og motkrafta til F2 er F2*. Så disse kraftpara er like store men motsatt retta. Og då kan vi også sjå på kraftsummen på tauet, som er F1 - F2*. Denne kraftsummen vil også bli mindre og mindre ettersom vi lar massen bli mindre. Så i grensetilfellet når massen nærmar seg null vil altså også kraftsummen nærma seg null, slik vi fant ut over.

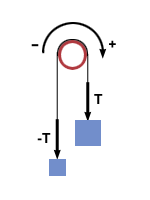
Trinser

I oppgavene kan vi tenkja at trinsene bare endrar retningen på snorkrafta, dei endrar ikkje størrelsen på krafta. Men forutsetningen er altså at trinsa er masselaus og friksjonslaus. Grunnen til at trinsa må vera masselaus er at gjenstandar med masse ikkje bare har ein treghet som betyr motstand mot akselerasjon, men dei har også rotasjonstreghet, som betyr motstand mot å endra rotasjonen.

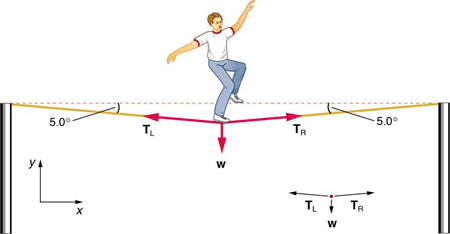
snorkraft

Snorkraft som vektorstørrelse

Snorkrafta virkar alltid i tauet sin retning. Og i eksempelet under må vi bruka vektorrekning for å finna snorkreftene TL og TR. Men vi kan likevel anta at dei har lik verdi.

snorkraft