Regula Falsi

Regula Falsi, eller "False Position Method", er ein iterativ metode for å finna eit nullpunkt til ein funksjon, dvs. finna ei løysing på likninga f(x) = 0. På same måten som for for halveringsmetoden,  må vi kjenna to punkt a og b på kvar side av nullpunktet, og som er slik at f(a) og f(b) har ulikt fortegn. Dessuten må funksjonen vera kontinuerlig i intervallet [a,b]. Men i staden for å finna midtpunktet, så finn vi det punktet der sekanten mellom punkta P_a =  (a, f(a)) og P_b = (b, f(b)) skjer x-aksen. Og på samme måten som ved halveringsmetoden, jobbar vi vidare med det intervallet der nullpunktet befinn seg. Sjå også Newtons metode.

Eksempel

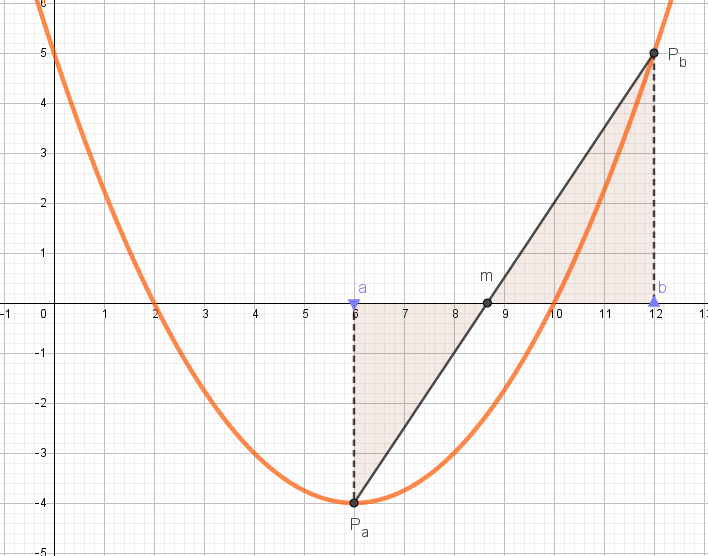
Først treng vi ein formel for skjeringspunktet m for linja mellom P_a og P_b. Dei to trekantane som er vist på figuren er likeforma. Det betyr at forholdet mellom høydene på trekantane er lik forholdet mellom breddene: - f(a) / f(b) = (m - a) / (b - m) eller - f(b) ( b - m) = f(b) (m - a). Her har vi brukt at høyden på den venstre trekanten er lik - f(a) sidan funksjonsverdien her er negativ. Når vi multipliserer ut, og løyser med hensyn på m, får vi då:

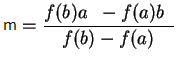
I vårt eksempel er a = 6, f(a) = - 4, b = 12 og f(b) = 5. Innsatt i formelen gir dette at m = (5*6 + 4 * 12) / 9 = 79/9 = 8,67. No legg vi merke til at nullpunktet ligg i intervallet [m, b]. Det betyr at no kan vi setja a = m og fortsetja:

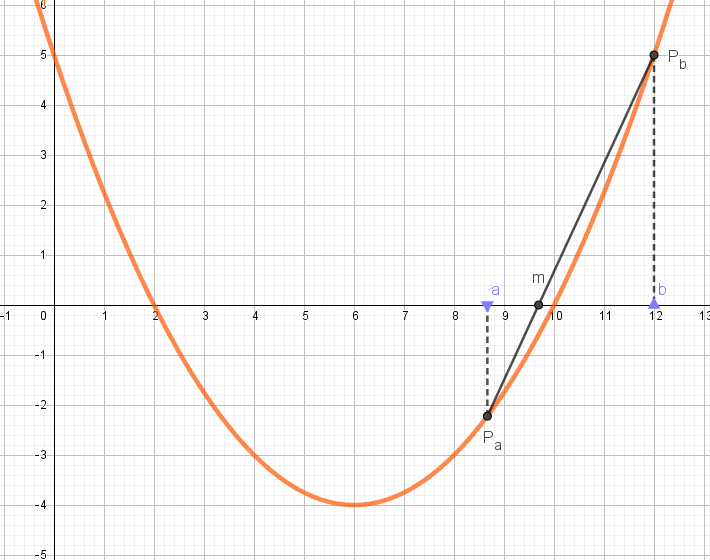
Hvis vi no bruker dei nye verdiane for a  og f(a), dvs a = 8,67 og f(a) = - 2,22 får vi den nye verdien m = 9,69. Slik kan vi fortsetja til vi er nær nok. Du kan prøva ut metoden her.

Algoritme

Ein algoritme i pseudokode kan då sjå slik ut. Merk at hvis produktet mellom f(a) og f(b) er negativt, så har dei ulikt fortegn!

    Gitt funksjonen f, a og b.
        gjenta til a,b er nær nok nullpunktet
        	m ← (f(b)a - f(a)b)/(f(b)-f(a)
        	hvis f(a)f(m) < 0
        		b ← m
        	ellers
        		a ← m
    

LENKER

REGULA-FALSI METHOD.