Newton Raphson-metoden

Newton-Raphson metoden (også kjent som Newtons metode) er ein numerisk metode for å finne nullpunkt for ein funksjon, dvs. å løysa likninga f(x) = 0

Metoden begynner med at vi gjettar på ein verdi x₀, som er nær* nullpunktet. Deretter finn vi ein betre verdi x₁ved å rekna ut

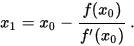
Denne prosessen kan vi gjenta så mange ganger vi treng. For kvar verdi x_n, så er den neste gitt ved
 

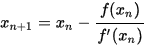
* Vi skal sjå litt meir på kva "nær" betyr nedanfor.

Geometrisk forklaring

Figuren under viser korleis iterasjonssteget i prosessen fungerer, dvs korleis vi går frå x_n til neste x-verdi x_n+1:

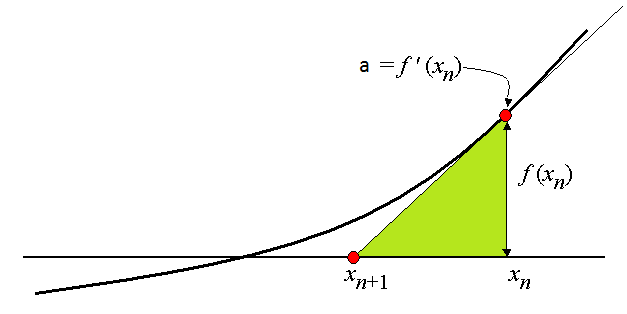
Vi tegnar inn tangenten til f(x) i punktet x = x_n. Linja har stigningstal lik a = f'(x_n). Men stigningstalet er også forholdet mellom høyden og bredden i den grøne trekanten, dvs.
 f'(x_n) = f(x_n) / (x_n - x_n+1).
Når vi ordnar på denne likninga får vi formelen vår:

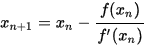
Vi har no funne eit punkt x_n+1 som er nærmare nullpunktet enn x_n var, og vi kan fortsetja prosedyren.

Eksempel

La oss sjå på på funksjonen f(x) = x³ -2x +2. (sjå figur under) Vi deriverer og får f'(x) = 3x² -2. Hvis vi no gjettar på talet x₀ =  -1, så treng vi å rekna ut f(-1) = 3, og f'(x) = 1. Då gir formelen oss x₁ = -1 - 3/1 = -4.
Deretter får vi sekvensen (avrunda til tre desimaler)  x₂ = -2.826, x₃ = -2.147, x₄ = -1.842, x₅ = -1.773, x₆ = -1.769,og då er vi allerede omtrent på nullpunktet. Du kan studera dette eksempelet nærmare sjøl.

Vi fant altså svaret (med tre desimalers nøyaktighet) etter bare seks steg, og det viser at metoden konvergerer raskt. Spørsmålet er om den alltid konvergerer?

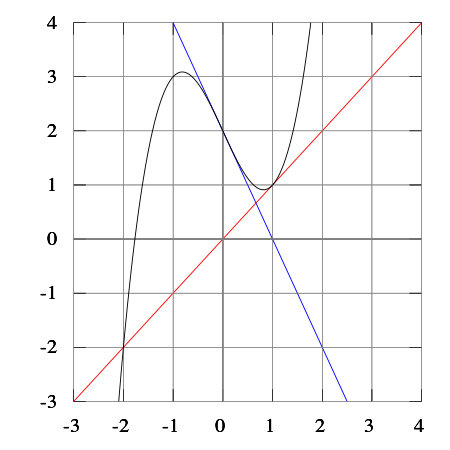
For å svara på det, kan vi sjå kva som skjer når vi gjettar på x₀ = 1,  i staden for -1. Vi får : x₁ = 0, x₂ = 1, x₃ = 0, osv. Som vi forstår: denne sekvensen vil alternera mellom 0 og 1 i det uendelige. Det vil sei at svaret er nei: metoden konvergerer ikkje alltid mot nullpunktet. Hvis vi startar i nærheten av punkta x = 0 eller x = 1, kan vi også bli dradd inn mot disse punkta og til slutt havna i same syklusen som over. Prøv feks x =1.1

Funksjonen har eit lokalt maksimum i x = -0.8165, og eit lokalt minimum i x = -0.8165. Hvis vi tilfeldigvis gjettar på eit slik stasjonært punkt, veit vi at den deriverte er lik null- (f'(x) = 0). Då vil metoden også feila, fordi vi prøver å dela på null. Hvis vi gjettar på x-verdiar i mellom disse punkta, vil tangenten ha negativt stigningstal, og havnar vi lenger ute på x-aksen. Dette kan noken gonger gå bra likevel fordi den neste iterasjonen vil bringa oss nærmare, men som regel vil det feila.