KEPLERS LOVER

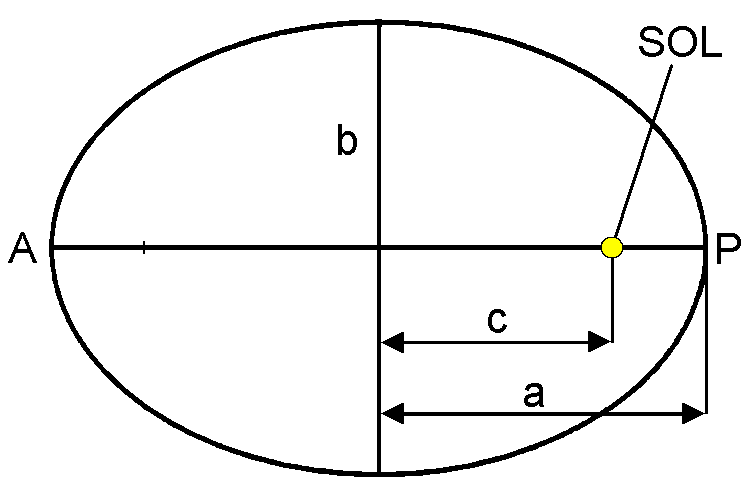
 Figuren til høgre viser ein ellipseforma bane der a og b kallast henholdsvis store og lille halvakse. a er også lik planetens gjennomsnittlige avstand til sola, og kan skrivast a = (r_max + r_min)/2. c er brennpunktets avstand frå aksesenteteret. Jo større forskjell det er på disse aksane, jo meir avlang blir ellipsen. Vi kan altså ta forholdet mellom b og a som eit mål for kor avlang ellipsen er. Men det er vanlig å heller bruka forholdet mellom c og a. Dette kallast for banens eksentrisitet e, og er gitt ved uttrykket:

Eksentrisisteten er eit tal mellom 0 og 1. Dersom den er lik 0, dvs at c = 0, betyr det at banen er sirkulær og har en konstant avstand r = a frå sola. I solsystemet er det Venus som har den mest sirkulære banen med ein eksentrisitet på 0.0067. Jordbanen er også nesten sirkulær og har ein eksentrisitet på 0.017 og, mens Pluto har den mest avlange planetbanen med ein eksentrisitet 0.2482. Likevel er dette lite samanlikna med kometane som ofte har svært avlange banar. Mars har ein eksentrisitet på 0.0934.

På figuren er punktet A det punktet i banen der planeta er lengst frå sola. Dette kallast for aphel. Tilsvarande er P det punktet i banen der planeta er nærast sola. Dette kallast for perihel. For ein elliptisk bane rundt jorda, dvs. ein satelittbane, blir disse punkta kalt hhv. apogeum og perigeum.

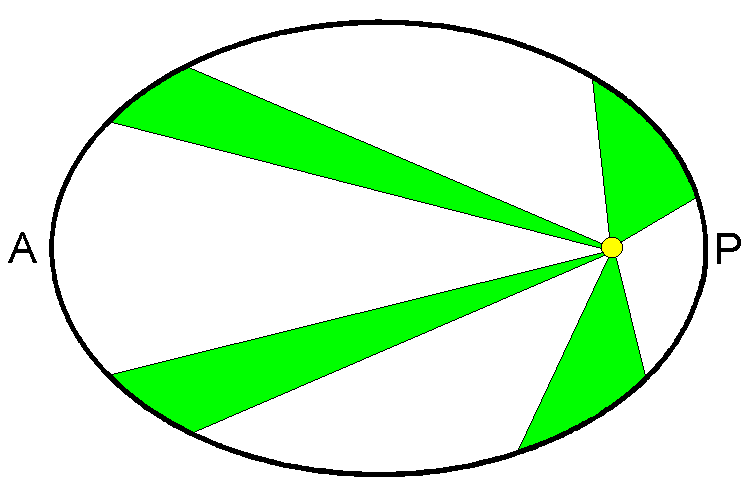
For ein satelitt er hastigheten størst i P og minst i A. Kor mykje større er gitt ved Keples andre lov:

Årsaken til denne hastighetsvariasjonen er at for ein elliptisk bane står ikkje gravitasjonskrafta normalt på banen slik tilfellet er for ein sirkulær bane. Dermed gjer gravitasjonskrafta eit positivt arbeid på satelitten når den er på vei mot jorda, og eit negativt på vei bort. Det betyr at når satelitten nærmar seg så aukar den kinetiske energien, og når den fjernar seg så minkar energien, og dermed også farten. Ein annan måte å sjå dette på er at når satelitten er langt borte er den potensielle energien stor. Sidan den totale mekaniske energien er bevart, så må den kinetiske energien vera tilsvarande liten.

Keplers andre lov seier altså at ein satellitt brukar mest tid i deler av banen lengst ute fra jordas sentrum, men den seier ingenting om kor lang tid den brukar på ein heil runde. Men her kjem Keplers tredje lov inn:

Bevis for Keplers tredje lov i et spesialtilfelle

Keplers lover er idealiserte og gjeld kun for ein punktmasse i bane rundt et tyngdesenter som også kan betraktast som ein punktmasse. Verkeligheten er meir komplisert, for det første fordi jorda har ujevn massefordeling og for det andre fordi at gravitasjonskrefter frå andre planeter spelar inn. Likevel kan vi bruka dei med god tilnærming både for planeter i bane rundt sola og satelittar i bane rundt jorda, og både for sterkt avlange banar og sirkelbanar.

Lovene er empiriske, men vart seinare vist generelt av Isaac Newton med utgangspunkt i hans gravitasjonslov. Men her skal vi nøya oss med å visa det for ein sirkelbane. Vi tar då utgangspunkt i at banefarten til ein satelitt som går i ein sirkulær jordbane (dvs. sirklingsfarten)  kan skrivast som

der M er jordmassen, G er den universelle gravitasjonskonstanten, og r er avstanden til jordensenteret. Hvis vi set farten lik banens lengde dividert med perioden, altså v =  2πr/T, får vi denne samanhengen mellom T og r:

Som vi ser, er dette i samsvar med Keplers tredje lov sidan radiusen r = a for ein sirkulær bane. Av dette ser vi også at konstanten K har verdien

Denne K-verdien gjeld for alle gjenstandar i bane rundt jorda. For planeter rundt sola må vi setja M lik  solmassen.

Utrekningar etter Kepler tredje lov

Når ein bruker den tredje loven er det ofte enklast å bruka andre enheter enn meter og sekund. Dersom vi reknar omløpstida i år og avstander i den astronomiske enheten AU, blir Keplers tredje lov forenkla. Med disse enhetene har både T og a verdien 1 for jorda. Dermed må også K vera lik 1, og vi kan skriva Keplers tredje lov slik:

T² = r³

Dette gjeld også for dei andre planetene. Tar vi td. utgangspunkt i omløpstida for Mars, som er 1.88 år kan vi finna r som:

r = T^2/3 = (1.88)^2/3 = 1.52 AU

som er akkurat gjennomsnittsavstanden til Mars.

Tilsvarande kan vi finna omløpstida for Pluto når vi kjenner den gjennomsnittlige avstanden til sola, som er 39.44 AU. Vi har då at

T = r^3/2 = (39.44)^3/2 = 248 år.

som stemmer med den observerte omløpstida for Pluto. Slå opp i tabellen og sjekk at verdiane for dei andre planetene også stemmer.