Fraktaler

Mange objekt i naturen, slik som ei bregne, er bygd opp av mønster som gjentar seg eller liknar seg sjøl i ulike skalaer. Dette kallar vi fraktaler. Vi forstår best strukturen ved å studera eit par-tre eksempel.

Koch-snøflaket

Først ser vi på det såkalte Koch-snøflaket, oppkalt etter den svenske matematikaren Helge von Koch.For å laga det, startar vi med den likesida trekanten til venstre, og lar det "voksa ut" ein likeformet trekant på kvar endeflate som er en nidel av den første (når vi reknar i areal). Det gir oss figuren i midten. Lar vi det "voksa ut" nye trekantar som er ytterligare ein nidel av dei forrige, får vi ein figur slik den til høgre. Hvis vi tenkjer oss at dette fortset i det uendelige, får vi til slutt ein figur som kallast Kochs snøflak, som er ein fraktal som har bestemte egenskaper. Det eine er at når vi fortset å dela opp sidene i det uendelige blir det ingen rette sider igjen. Koch-snøflaket er altså ein figur som bare består av hjørner! 

Hvis vi lar arealet av den første trekanten vera 1 så må den midterste figuren ha arealet 1 + 3/9. Den neste figuren har arealet 1 + 3/9 + 12/81. For kvart steg legg vi til fire gonger så mange trekanter som i leddet før (bortsett fra ledd to), og disse trekantane er i størrelse alltid ein nidel av de forrige. Dette er ei geometrisk rekke med a = 3/4 og k = 4/9. Og sidan k < 1 vil den konvergera. Summen blir S = 0.75/(1-4/9) = 1.35.
Arealet er altså endelig, sjøl om vi legg til uendelig mange småbitar.

Denne er enklere å rekna ut. For kvart steg legg vi til 1/3 av det vi hadde før, med andre ord har vi at omkretsen i steg n er 4/3 av forrige. Vi forstår då at når n går mot uendelig vil også omkretsen gå mot uendelig. Vi har altså ein figur som har endelig areal, men uendelig omkrets.

Sierpinski-trekanten

Som om ikkje dette er rart nok, så kan det bli rarare. La oss sjå litt på ein annan fraktal som kallast for Sierpinski-trekanten, oppkalla etter den polske matematikaren  Wacław Sierpiński:

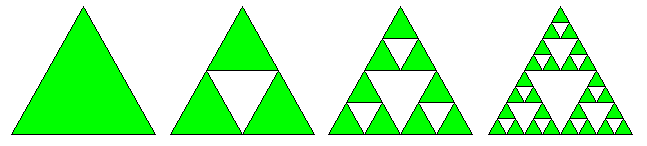
Her startar vi også med ein likesida trekant. Så deler vi opp trekanten i fire like trekanter og fjerner den midterste. Deretter deler vi dei tre gjenværande i fire nye og fjernar igjen den midterste. Denne prosessen tenkjer vi så held på i det uendelige, og den figuren vi står igjen med kallast Sierpinski-trekanten. Det viser seg at denne har uendelig kantlinje, men likevel er arealet lik null.

Fraktale planter og vekst i naturen.

Hvis vi forstørrer ein av av dei tre første del-trekantane i Sierpinski-trekanten så oppdagar vi at den er identisk til trekanten i seg sjøl. Dette er ein karakteristisk egenskap ved fraktaler. På samme måten oppdagar vi at hvis vi zoomer inn på ein del av Koch-snøflaket ser vi at mønsteret gjentar seg sjøl i det uendelige. Dette er også tilfellet for det vi kan kalla fraktale planter. Eit eksempel på dette er den såkalte Barnsley-bregna. Ei slik fraktal bregne er slik at kvar grein av bregna er lik bregna sjøl. Felles for disse tre eksempela er at dei lar seg generera ved hjelp av ein enkel rekursiv prosedyre, og er derfor velegna for å tegnast vha eit dataprogram. Barnsley-bregna kan lagast ved eit såkalt L-system, eller Lindenmayersystem. Og naturligvis er det også oppkalla - denne gongen etter ein biolog - den ungarske Aristid Lindenmayer.

Hvis vi overfører dette oppbyggingsprinsippet til korleis menneskehjernen utviklar seg, så er det nærliggande å tru at det også spelar ein rolle her. For, som eg skriv i artikkelen Optimalisering av nettverkstopologi,  så er det ikkje nok informasjon i våre gener til å beskriva den komplekse strukturen i hjernen. Derfor må hjernen sin struktur vera generert ved hjelp av ein form for regel eller oppskrift. For på samme måten som ein beskrivelse av strukturen til Barnsley-bregne vil ta mykje plass, så er det faktisk fort gjort å beskriva oppskriften for korleis den blir laga.    

Julia og Mandelbrot-mengdene

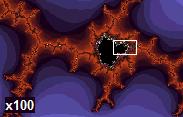
Til slutt ein liten kikk på det som antagelig er dei mest berømte av fraktaler, nemlig Julia- og Mandelbrot-mengdene. Disse er sjølsagt også oppkalt etter matematikarar, nemlig den polsk-fødte Benoit Mandelbrot, og den franske  Gaston Julia. Under er fire bilder av Mandelbrot-mengden. Her viser vi fire figurar med aukande forstørringsgrad. Vi ser at når vi zoomer inn så dukkar det opp eit mønster som er veldig likt det opprinnelige.

Til sist bare eit bilde av Juila-mengde, bare for å visa kor vakker den er:

EKSTERNE LENKER (Wikipedia)

Fractal
Koch snowflake
Sierpinski triangle
Barnsley Fern
L-system
Mandelbrot set
Julia set.