Lindenmayersystem (L-system)

I 1968 introduserte den ungarske biologen Aristid Lindenmayer eit system for å modellera plantecelle- og plantevekst. Dette kallast i dag for Lindenmayersystem eller ofte bare L-system. I 1990 publiserte han boka The Algorithmic Beauty of Plants saman med Przemyslaw Prusinkiewicz som beskriv dette. Men L-system har også blitt brukt til alt frå å modellera elvesystem til å komponera musikk.

Reglar

Et Lindenmayersystem er ein bestemt type formell grammatikk (Formal grammar). Formelle grammatikkar blir brukt innan informatikk og lingvistikk. Dei består av et sett formasjonsregler som definerer kva strenger frå alfabetet til eit formelt språk som er syntaktisk gyldige (det vil sei grammatikalske) i dette språket. Noam Chomsky delte i 1956 inn formelle grammatikkar i ulike typer, og plasserte dei i det som er kjent som Chomskyhierarkiet. Ein formell grammatikk definerer ikkje betydningen av disse strengene, bare formen.

Eit Lindenmayersystem består av:

eit alfabet A som består av eit sett med symboler. Noken av disse symbola kan bli erstatta av andre, mens andre kan ikkje. Dei siste blir kalla "konstantar" eller "terminalar".
eit startaksiom S som er ein streng beståande av symboler frå A
eit sett med produksjonsreglar P fortel korleis kvart symbol frå A kan erstattast av andre. Merk at konstantane ikkje treng nokon regel.

Eksempel 1: Algevekst

Lindenmayer sitt originale L-system for å modellera algevekst ser slik ut.

    variable : A B
    konstantar : ingen
    aksiom : A
    produksjonsreglar : (A → AB), (B → A)

Produksjonsreglane blir brukt iterativt, og startar med aksiomet. Så mange reglar som mulig blir brukt for kvar iterasjon. Dette gir følgande strengar:

    n = 0 : A
    n = 1 : AB
    n = 2 : ABA
    n = 3 : ABAAB
    n = 4 : ABAABABA

Forklaring: I første iterasjon kan bare den første regelen brukast, og vi får strengen AB. I neste iterasjon kan begge reglane brukast, slik at A blir til AB og B blir til A, og dette gir strengen ABA. Og slik går no dagane.

Eksempel 2: Geometrisk tolking

Sidan L-system er rekursive av natur, gir det oss mulighet til å laga mønster som gjentar seg sjøl i ulik skala, med andre ord fraktaler. For å kunna tegna disse blir symbola tolka som instrukser til ein tegnealgoritme. I dette eksempelet brukest symbola 0, 1, [ og ], men vi kunne like gjerne ha brukt fire andre, fordi det er strukturen (og her, tolkingen av den) som er av betydning.

    variable : 0, 1
    konstantar: [, ]
    aksiom : 0
    produksjonsreglar : (1 → 11), (0 → 1[0]0)

n = 0:     0
n = 1:     1[0]0
n = 2:     11[1[0]0]1[0]0
n = 3:     1111[11[1[0]0]1[0]0]11[1[0]0]1[0]0

Tolking:

For å tegna ein streng, bruker ein ofte såkalt Turtle-graphics der ein tenkjer seg ei virtuell "Turtle" (eller faktisk har ei robot-Turtle). I utgangspunktet står denne i ein bestemt posisjon, og har ein bestemt retning. Så kan den flytta seg eit steg fram i den retningen mens den tegnar ein strek. Den kan også snu seg til høgre eller venstre med ein bestem vinkel, og den kan flytta seg tilbake til ein tidligare posisjon. For å huska posisjonar bruker vi ein såkalt LIFO-stack. (stakk eller stabel) Tenk deg at du har ein stabel med tallerkar. Når du lagrar ein ny tallerken legg du den på toppen. Dette kallast push i dataspråket. Hvis du vil henta tilbake ein tallerken, så må den hentast frå toppen. Dette kallast pop. På denne måten vil du alltid henta tilbake den du sist lagra, og derfor kallast denne formen for stack for LIFO, som står for Last In First Out. Dei fire symbola i alfabetet kan då tolkast slik:

0: tegn eit linjesegment som (evt.) sluttar i eit lauv.
1: tegn eit linjesegment
[: push posisjon og vinkel, og snu 45 grader til venstre.
]: pop position og vinkel, og snu 45 grader til høgre.

I henhold til disse reglane, kan vi tegna strengen for generasjon 3 slik:

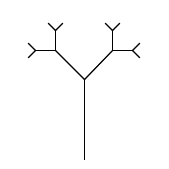
turtle3

Ved å bruka eit passande alfabet, reglar og tolking, kan ein tegna mange forskjellige typar vekster, men også heilt andre figurar (også i 3D) som for eksempel Koch-snøflaket, Sierpinski-trekanten eller Hilbert-kurven. Sjå interaktive eksempel på dette.

Plantevekst og variasjon

Planter og plantedeler er ofte modulære, dvs. at dei består av modular (greiner, lauv, blomar osv) som blir kobla saman og som gjentar seg. Greiner deler seg og dannar nye greiner osv. Måten nye greiner / modular blir lagt til, skjer ikkje heilt tilfeldig, men følgjer bestemte mønster for forgreining som definerer plantens form. Dette egnar seg godt til å bli modellert av eit L-system. (6)

Men planter veks ikkje slavisk etter ein algoritme. Dei følgjer eit grunnmønster, men viser stor variasjon likevel. Men dette kan også modellerast. Hvis den regelen som blir brukt for eit bestemt symbol er avhengig av kva symbol som ligg til høgre og venstre for det aktuelle symbolet, seier vi at systemet er kontekstsensitivt. Dette gir meir variasjon i veksten. Dette er også tilfellet for stokastiske system der det er meir enn ein regel for kvar av symbola, og kvar regel blir anvendt med ein viss sannsynlighet. For å gi ytterligare realisme kan ein også trekkja inn effekten av insektangrep, tørke, vind osv.

Menneskekroppen

Også deler av menneskekroppen ser ut til å ha ein fraktal-liknande struktur. Eksempel er lungene, blodåresystemet, nyrene og hjernen. Derfor er det nærliggjande å prøva L-system også når vi skal simulera vekst av slike organer. Nevrale nett er ein veldig enkel modell for biologiske nervenett, og strukturen på nettet har betydning for kor godt det fungerer. Her kan ein bruka Genetiske Algoritmar for å optimalisera strukturen. For små nett kan ein då operera på synapse-nivå, dvs. at kvar enkelt kobling blir bestemt av den genetiske algoritmen. For større nett vil dette hverken vera effektivt eller realistisk. For det er ikkje slik naturen fungerer. Ein kunne tenkja seg at alle koblingane i hjernen var bestemt av DNA. Men det er simpelthen ikkje nok informasjon i DNAet til å bestemma alle koblingane. Ein reknar med at det fins i størrelsesordenen 10¹⁴ synapsar i hjernen, mens vårt DNA har 10¹⁰ bits informasjon. Derfor gir det meining å bruka L-system eller liknande algoritmer. Ein kan tenkja seg å la den genetiske algoritmen finna dei optimale produksjonsreglane for L-systemet. Sjå ref. (5) og (6).

LENKER

1) L-system på Wikipedia.

2) L-systems: from the Theory to Visual Models of Plants. (PDF)

3) Plant bodies - building plants from cells and modules.

4) Basic Body Plan of Flowering Plant.

5) Searching Neural Network Structures with L-systems and Genetic Algorithms.

6) Evolving Artificial Neural Networks through L-System and Evolutionary Computation. (PDF)

Python eksempel

Lindenmayer Systems - A Python Adventure.

Modeling Plants with Lindenmayer Systems.

turtle — Turtle graphics. Eit Python bibliotek.

BOK

The Fractal Geometry of the Brain.