Tallsystem og representasjon av data
20 september 2017Titallsystemet
Når vi skriv tal, så bruker vi vanligvis titallsystemet. Det betyr for det første at vi har ti mulige siffer å velja blant, nemlig 0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. For det andre betyr det at vi bruker et plass-siffersystem der kvart plass representerer ein tierpotens. Du har sikkert høyrt om enerplass, tierplass osv. Vi kan plassera talet 356 inn i ein tabell slik:
| hundreplass | tierplass | enerplass |
|---|---|---|
| 3 |
5 |
6 |
Ved hjelp av denne tabellen kan vi omskriva 356 som: 3*100 + 5*10 +
6*1 = 3*102 + 5*101 + 6 *100
Merk at her har vi skrive 10 som 101, og 1 som 100.
Dei neste plassane i systemet er stadig høgare potensar av 10.
tusenplassen er 103 osv.
Totallsystemet
Men det fins andre måtar å skriva tal på. Innen data er det vanlig å bruka totallsystemet, eller det binære tallsystemet. Då har vi bare to typer siffer til rådighet, nemlig 0 og 1. På dataspråket kallar vi eit enkelt binært siffer for ein bit. Når vi tel med vanlige tal kan kjem vi heilt opp til 9 før vi må begynna med to siffer. Det neste talet etter 9 skriv som 10. Men med binære tal må vi bruka to siffer allerede etter 1! Det neste talet, dvs. 2, må vi då med totallsystemet skriva "10". Vi seier ikkje ti, men ein - null, og for å unngå misforståelse skriv vi ofte 102. Etter 2 kjem 3 som vi på "binærsk" skriv 112. Så langt kjem vi med to siffer. 4 må vi skriva med tre siffer: 1002. Deretter kjem 5 = 1012, 6 = 1102 og 7 = 1112.
| Vanlig | Binær |
|---|---|
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Til høgre er ein tabell som viser dei første ti tala med vanlige og med binære tal. Her har vi tatt med såkalte ledande nullar. Disse reknar vi jo ikkje med. 0001 = 1 osv. Hvis vi ser litt nærmare på talet 7 = 1112, så merkjer vi oss at vi kan skriva det som summen 1002 + 0102 + 0012, og dette er med vanlige tall lik 4 + 2 + 1. Disse er alle potenser av 2: 4 = 22, 2 = 21 og 1 = 20. Dei tre første plassane i det binære tallsystemet er altså (i stigande rekkefølge) enerplassen, toerplassen og firerplassen. Når vi samanliknar med titallsystemet, så ser vi at den neste plassen blir 23 = 8, og så kjem 24 = 16 osv. La oss putta det binære tallet 101001 inn i ein tabell som den over:
| 32plass | 16plass | åtterplass | firerplass | toerplass | enerplass |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 1 |
Talet vi får blir då: 1*32 + 0*16 + 1*8 + 0*4 + 0*2 + 1*1 = 32+8+1 = 41. På denne måten kan vi rekna om eit binært tal til eit vanlig tal. Her kan du prøva ein kalkulator som reknar om mellom vanlige desimaltall og binære og andre tall. Den kan også rekna med hexadesimale tall, som vi skal sjå på nedanfor.
Kor mange bits treng vi?
Vi er ofte interessert i kor store tall vi får plass til med eit gitt antal siffer, dvs bits. Vi såg over at med to siffer er antalet 4. Aukar vi med et siffer, så får vi 8 mulige tal (0-7), altså det doble. Og det forstår vi lett når vi ser at tala 4 - 7 bare gjentar det samme bitmønsteret som 0 - 3, bare med ein "1" framfor. Kvar ekstra bit gir altså dobbelt så mange tal. Med litt tankearbeid ser vi då at når 4 siffer gir 16, og 5 gir 32, så er formelen rett og slett 2n. I data blir bits gruppert i grupper på 8 som vi kallar ein byte (B). Ein byte kan då ifølge formelen innehalda 28 = 256 tall. Dette kan td. vera heiltala frå 0 til og med 255. Ein CD har 16 bits oppløysing, og det gir altså 216 = 65 536 ulike nivå på kvar lydsampling. (les meir om Digital lyd.).
Enhet og prefiks
Det er tillatt å bruka liten bokstav b for bits, men det er anbefalt å skriva fullt ut bits for å skilla det frå Byte, der vi bruker den store bokstaven B.
Når det blir veldig mange bits eller bytes, så bruker vi som regel eit prefiks. For eksempel kan ein CD ha plass til ca. 700MB, mens dagens harddiskar ofte kan lagra mange Terabyte. Disse prefiksa har i dag same betydning som i matematikk og fysikk. k (kilo) = tusen, M (Mega) = en million, G (Giga) = en milliard, og T (Tera) = billion, osv.
Sekstentallsystemet
Men det fins også andre tallsystem som er nyttige i data. Eit av dei er sekstentallsystemet, eller det hexadesimale systemet. Her har vi, som navnet tilseier, 16 ulike siffer å bruka på kvar plass. Vi bruler vanlige tall frå 0 - 9 pluss dei seks første bokstavane i alfabetet. Det betyr at A = 10, B = 11, C = 12, D = 13, E = 14 og F = 15. Du kan også bruka små bokstaver. Med eit siffer frå 0 - F, kan vi altså skriva tala frå 0 - 15. Frå og med 16 må vi ta i bruk fleire siffer. 16 skriv vi som 1016, der "16" er tatt med for å visa ka tallsystem vi bruker. Dei neste tala blir då 17 = 1116 18 = 1216 osv. opp til 1F16, som då er lik 31. No må vi auka andre sifferet slik at 32 = 2016. Med to siffer kan vi altså skriva tal heilt opp til 255 = FF16. Systemet er då heilt analogt med totallsystemet, bare at vi har 16 siffer, og plassane står for (frå høgre mot venstre) for enerplass, 16-plass, 256-plass, 4096-plass osv. Dette fordi 256 = 162 og 4096 = 163 osv. Som eksempel kan vi no rekna om det hexadesimale talet C3D16 til vanlig desimaltal ved hjelp av følgande tabell:
| 256-plass | 16-plass | enerplass |
|---|---|---|
| C |
3 |
D |
Sidan C = 12 og D = 13, så betyr dette 12*162 + 3*161 + D*160 = 3133. No kan du sjøl forska vidare på dette ved hjelp av kalkulatoren. Fargar og hexkode. Når vi skal definera fargar i ei webside, feks. til tekst, så kan ein bruka hex-kode til å sei kor mykje av primærfargane rødt, grønt og blått ein vil bruka. Her bruker vi to hex-siffer. Det vil sei at vi bruker tal frå 0 (00) til 255 (FF) for å angi kor mykje av kvar farge vi vil ha. Fargen #ff7900 betyr derfor 255 deler, (dvs. 100%) rødt, 121 deler grønt, og ingenting blått. Det gir ein oransje farge. Du kan testa ut ulike kombinasjonar ved hjelp av denne RGB-utforskaren.
Åttetallsystemet
Hvis du har fulgt med så langt, bør det ikkje komma som ein overraskelse at vi kan laga uendelig mange tallsystem, med kvar sin base. I data er også åttetallsystemet, eller det oktale tallsystemet brukt. Her har vi siffera frå 0 til 7 til rådighet. Når vi kjem over 7 må bruka to siffer, slik at åtte blir 10, ni blir 11 osv. Den einaste forskjellen frå dei tre andre plass-siffersystema vi har sett på er det tallet kvar plass representerer. I titallsystemet er plassane 1, 10, 100, 1000 osv. For kvar plass til venstre gangar vi med ti. I totallsystemet gangar vi med 2, slik at plassane er 1, 2, 4 8, 16 osv. Så vi bruker det same prinsippet for åttetalsystemet: vi startar med ein og multipliserer med 8 for kvar plass. Dermed får vi plassane 1, 8, 8 * 8 = 64, 8 * 64 = 512 osv. Talet 17508 er derfor det same som 1*512 + 7*64 + 5*8 + 0*1 = 1000 i titallsystemet.
Lagring av data
 Når disse einarane og nullane
skal lagrast på eit lagringsmedium eller overførast gjennom ein kabel,
så er poenget å representera ein "null" eller ein "ein" som to
distinkte fysiske tilstandar. I gamle dagar vart for eksempel
data ofte lagra på hullbånd
eller hullkort,
der ein "1" vart representert ved eit hol i båndet / kortet (eller
omvendt, eg er ikkje sikker). På bildet til høgre kan du sjå korleis
ordet "Wikipedia" kunne lagrast på eit bånd. Eit anna eksempel er det
såkalte magnetkjerneminne
som vart brukt ganske lenge som arbeidsminne i datamaskinene. Her blir
ein bit lagra vha ein magnetisk ring kan magnetiserast i to retningar.
Begge disse eksempela er fundamentale i datamaskinens
historie
Når disse einarane og nullane
skal lagrast på eit lagringsmedium eller overførast gjennom ein kabel,
så er poenget å representera ein "null" eller ein "ein" som to
distinkte fysiske tilstandar. I gamle dagar vart for eksempel
data ofte lagra på hullbånd
eller hullkort,
der ein "1" vart representert ved eit hol i båndet / kortet (eller
omvendt, eg er ikkje sikker). På bildet til høgre kan du sjå korleis
ordet "Wikipedia" kunne lagrast på eit bånd. Eit anna eksempel er det
såkalte magnetkjerneminne
som vart brukt ganske lenge som arbeidsminne i datamaskinene. Her blir
ein bit lagra vha ein magnetisk ring kan magnetiserast i to retningar.
Begge disse eksempela er fundamentale i datamaskinens
historie
I dag er prinsippet for ein tradisjonell harddisk å magnetisera små
segment av disken i ein av to retningar. Så blir den eine retningen
definert som 0 og den andre som 1. Disse retningane kan endrast ved
skriving, ellers målast ved lesing, og magnetiseringen er permanent
slik at data ikkje forsvinn når datamaskinen blir slått av. Derfor
egnar det seg som permanent datalager. Moderne diskar bruker såkalt Giant
magnetoresistance (GMR) som er meir raffinert, men er i
prinsippet det same: å lagra 1 og 0 som to forskjellige magnetiske
mønster på disken. Ein tradisjonell harddisk HDD,
bruker ei roterande magnetisk plate, der ein liten skrive / lesearm
kan bevega seg nær det magnetiske for enten å avlesa mønsteret eller
endra det.
Flash-minne
benytter seg av tilstandar i transistorar. Det fins mange typar og
anvendelsar: det blir brukt i datamaskinens hovedminne , minnebrikker,
minnepennar
og SSD-diskar
(solid-state drive), som er ein harddisk uten bevegelige deler.
Fordelen med flash-minne er at det er hurtigare enn den gamle
harddisken. Ein bakdel har vore prisen og meir begrensinga
lagringsplass, men dette endrar seg hurtig - så hurtig at det i nær
framtid kanskje vil bli slutt på skillet mellom hoved (intern-) minne
og eksternt lager.
Ein CD består av eit spor med ei rekkje "humper" (boka skriv at der er groper, men frå den sida laseren les er det humper) som blir lest av vha ein laserstråle. Sporet går frå innerst til ytterst, og er så smalt at det ville vore nesten 5 km langt hvis du strekte det ut! Ein bit blir ikkje representert ved humpane i seg sjøl (slik boka påstår), men i overgangane. Laserene skannar overflata og når ein hump begynner eller slutter får vi ein "1", resten er nullar. På figuren under kan du sjå korleis humpane blir oversatt til ein bitstraum.
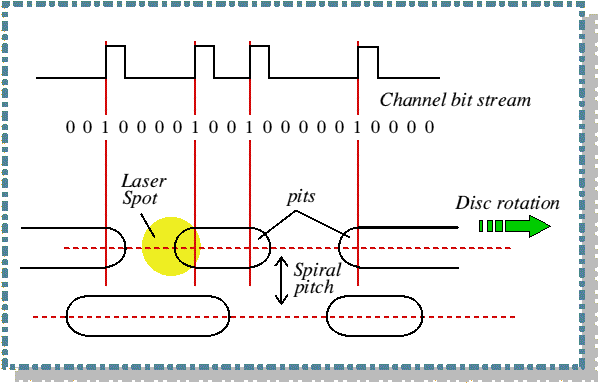
Eit slikt signal kan overførst vha eit digitalt signal, der einarar blir representert ved eit "høg" spenning, mens nullarar blir representert ved ein "lav" spenning td, 0. Sjå Digital lyd.
LENKER
Binært tallsystemVideo om tallsystem
Teljing med binære tal
