Langtons maur

Langtons maur er ein enkel virtuell "maur" som i originalversjonen beveger seg i eit rutemønster med svarte og kvite ruter i henhold til veldig enkle reglar. Likevel framviser den kompleks emergent "oppførsel". Den vart oppfunnen av Chris Langton i 1986. I 2002 vart det bevist at den er ein universell Turingmaskin. Langtons maur kan generaliserast på mange måtar. Ein kan leggja til fleire fargar og tilstandar, ein kan endra reglane, endra på rutemønsteret, og ein kan la fleire maur bevega seg i same planet. Sjå lenker nedanfor. Langtons maur kan også beskrivast som ein cellulær automat.

Animasjon av dei første 200 stega til ein maur.

Reglar

I starten befinn mauren seg i ei tilfeldig rute, med ein tilfeldig retning, Den tar eit steg framover i den retningen, og vidare oppførsel er betinga av fargen på den ruta mauren er på:

• Hvis den er på ei kvit rute, snur den 90° til høgre, byter farge på ruta og går eit skritt fram
• Hvis den er på ei svart  rute, snur den 90° til venstre, byter farge på ruta og går eit skritt fram.

Mauren byter altså kvar gong farge på den ruta den befinn seg på: svarte ruter blir kvite, og kvite blir svarte.

Oppførsel:

Disse reglane er enkle, men fører likevel til ganske kompleks oppførsel. Når vi startar med ei heilt kvit flate ser vi tre distinkte mønster:

1. Enkelhet: I dei første få hundre stega skaper den veldig enkle mønster som ofte er symmetriske.
2. Kaos: Etter dette dannar det seg eit irregulært mønster som varer til rundt 10,000 steg.
3. Emergent orden: Til slutt begynner mauren å laga ein uendelig "motorvei" som består av 104 steg som gjentar seg.

Sjøl om vi startar med ei tilfeldig generert flate, ser det ut til at alle simuleringar konvergerer mot det same gjentakande mønsteret med ein slik motorvei. Utallige datasimuleringar viser dette kvar einaste gong. Men ingen har klart å bevisa at det må bli slik for alle mulige start-tilstandar, og det er heller ikkje sikkert at det er mulig å bevisa. Egentlig er dette litt oppsiktsvekkjande: Vi veit altså alt som det er mulig å vita om Langtons maur, fordi det er vi som lagar reglane den lever etter. Likevel veit vi ikkje alt om langtidsoppførselen når vi varierer startbetingelsane. Men det som er bevist, er at alle variantar er ubegrensa, i betydningen at mauren kjem lenger og lenger bort frå startpunktet sitt. Dette er kjent som Cohen–Kung teoremet. Dette gjeld altså for Langtons opprinnelige maur. Når vi utvider eller endrar reglane, så forandrar også oppførselen seg, som vi skal sjå.

Utvidelsar

1 Fleire fargar:

Greg Turk og Jim Propp foreslo å bruka fleire fargar på rutene, og la disse endra seg syklisk. Farge 1 blir til farge 2, farge 2 til 3 osv.*  Kvar farge må ha ein regel for om mauren skal snu til venstre eller høgre. Disse reglane kan samanfattast i ein enkel tekstreng med "L" eller "R".  For eksempel betyr tekststrengen "RLR" at når mauren kjem til ei rute med farge 1, så snur den til høgre og bytter til farge 2. Når den kjem til farge 2, så vil den svinga til venstre og skifta til farge 3. Og når den til slutt kjem til farge 3, så vil den svinga til høgre og skifta tilbake til farge 1. Langtons sin originale maur har derfor navnet "RL" i henhold til denne måten å beskriva reglane. Noken av disse reglane produserer mønster som blir symmetriske igjen og igjen. Eit av dei enklaste er regelen "RLLR". Du kan sjøl prøva ulike variantar i denne interaktive animasjonen. Du kan også sjekka ulike mønster å testa her.

2. Heksagonal grid

Hvis vi lar mauren vandra på på ei flate med sekskanta felt, så har den fleire retningar å snu seg i, og vi treng derfor fleire symbol for disse. Eksempelvis kan vi bruka N (for "No turn", dvs. rett fram), R1 (60° til høgre), R2 (120° til høgre), U (for "U-turn", dvs. 180°), L2 (120° til venstre) og L1 (60° til venstre). Prøv variantar av dette her. (Denne nettsida bruker andre symbol, jamfør figuren øverst)

Her er eksempel, henta frå Wikipedia, på kva mønster ulike reglar ihht. 1 og 2 kan produsera:

Kommentarer:

RLR: Gir kaotisk vekst. Det er ikkje kjent om denne varianten noken gong vil begynna å laga ein motorvei.
LLRR: Symmetrisk vekst.
LRRRRRLLR: Fyller rommet i ein firkant rundt seg sjøl.
LLRRRLRLRLLR: Skaper ein slags bølgete motorvei.
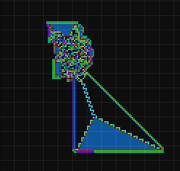
RRLLLRLLLRRR: Skaper ein fyllt trekant som veks og flyttar seg.
L2NNL1L2L1: Dette er på ein heksgonal grid, og resultatet er sirkulær vekst.
L1L2NUL2L1R2: Også heksagonal grid, men no får vi spiral-vekst.

Langtons maur i 3D

Det er naturlig å forsøkja seg å utvida også til tre dimensjonar. Det er ikkje opplagt korleis reglane skal vera i såfall, men denne artikkelen fortel at det kan oppstå mange forskjellige typer motorveier, og komplekse strukturar. Sjå eksempel på dette her (bla ned)

Fleire tilstandar

Fleire maur samtidig

Så langt har vi latt ein einslig maur vandra rundt åleine, men det fins sjølsagt folk som har testa med fleire maur. Dette gir opphav til endå meir komplekse strukturar, og noken gonger samarbeider maurane om dette, mens andre gonger vil ein maur rolig bygga ned det som ein annan har bygd opp. Der er ingen behov for konfliktløysing, for to maur som havnar på den same ruta vil gjera den same endringen i fargen (sjøl om dei har ein annan retning. Prøv ut dette her. (Merk at spilleplanet i dette eksempelet er slik at når ein maur går ut til høgre, så vil den dukka opp igjen til venstre, og tilsvarande vil ein maur som går opp dukka opp nede)

Kva kan vi læra av Langtons maur?

Bortsett frå at studiene av Langtons maur er artig og at den produerer intrikate  og vakre / forbløffande mønster, så er det kanskje noko djupare å læra her. Det eine er at Langtons maur demonstrerer prototypen på såkalt emergent oppførsel. Evnen til å byggja motorveier og andre komplekse strukturar er ikkje programmert inn i mauren, men likevel oppstår disse strukturane som følge av dei innebygde reglane. Det oppstår orden av kaos, uten at det er designa, akkurat som livet sjøl. Det andre (som heng saman med det første) er at sjøl om systemet vårt er deterministisk (alt som skjer er ein følge av reglane, og ingenting skjer tilfeldig) så har vi ingen måte å rekna ut om ein gitt startbetingelse fører til motorveibygging, og når dette evt, skjer. Vi forstår at determinisme og forutbestemmelighet er to forskjellige ting.

* Ein skulle tru at dette ikkje er nødvendig at farge nr n alltid blir til farge nr n+1, men eg kjenner ikkje til variantar som ikkje gjer det slik.

LENKER

Complex Projective 4-Space.

Complexity of Langton's ant.

Artig variant med diskusjon her.

Interaktiv heksagonal variant

Langtons maur og logiske porter Masteroppgave ved UiO.

Python script for generating 2D n-state Langton's Ant animations :)

Langton's Ants - in Javascript.

Endå ein interaktiv variant .

Langton's Ant A generization to multiple colors med simulering.