Introduksjon til funksjonar
7 februar 2016- Funksjonen som talmaskin
- Definisjonsmengde og verdimengde.
- Måter å uttrykkja ein funsjon: tabellform, graf eller formel
- Korleis finna definisjonsmengde og verdimengde?
- Enkel test om ein graf definerer ein funksjon
Funksjonen som talmaskin
Kva meiner vi egentlig med begrepet funksjon? Vi kan først sjå litt på ein (litt uformell) definisjon:
Definisjon: Ein funksjon er ein relasjon eller avbilding (ordet "mapping" blir også brukt) frå ei mengde til ei anna mengde på ein slik måte at det til kvart element i den første mengda blir tilordna eit element frå den andre. |
Når vi skal danna oss eit bilde av kva dette betyr i praksis, så er det ofte nyttig å tenkja på ein funksjon som ein slags "talmaskin" der du puttar tal inn, og får tal ut. (Ein funksjon kan i prinsippet også ta bokstaver og andre symboler som input eller output, men her begrensar vi oss altså til tal!) Vi gir som regel denne funksjonen eit navn, som f (kort for “funksjon”), og hvis vi kallar det talet vi putter for x, så skriv vi det talet som kjem ut for f (x). Slik kan vi tegna dette:
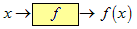
Funksjonsnotasjonen f (x) betyr “funksjon av x”. Talet x blir kalla argumentet til f, eller også den uavhengige variabelen, og det som kjem ut blir kalla verdien eller den avhengige variabelen. Vi bruker ofte også bokstaven y for verdien, og vi kan skriva at y = f(x).
Definisjonsmengde og verdimengde
For at vi skal kalla noke ein funksjon, så må eit krav vera oppfylt, nemlig at vi aldri kan få to forskjellige svar når vi puttar inn same tal. Puttar vi inn x = 2 og får ut f(2) = 5 ein gong, så må vi får ut 5 kvar gong. Funksjonsverdien er altså bare avhengig av x. Men omvendt kan det godt henda at to forskjellige x-ar kan gi same tall ut. Vi kan tegna dette slik:
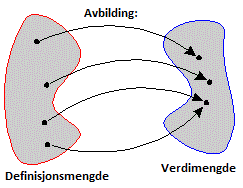
Mengden av alle mulige x-ar vi kan mata ein funksjon med kallar vi definisjonsmengden. Noken gonger kan det vera alle reelle tal, andre gonger kan det vera eit intervall, og atter andre gonger ei tellbare og endelig mengde. Mengden av alle mulige tal vi kan få ut kallar vi så verdimengden. Det som bestemmer verdimengden er for det første funksjonen sjøl, men også definisjonsmengden.
Måter å uttrykkja ein funksjon
Vår talmaskin må ha ein eller annan
regel, eller algoritme
som fortel den korleis den skal finna det riktige svaret for kvar x. Dette kan skje på fleire
måtar:
- Ein funksjon kan vera definert ved ein tabell,
spesielt hvis det er få verdiar. Her er eit eksempel på ein
funksjon f som er gitt
ved ein tabell:
Her er definisjonsmengden Df = {10, 2, 5} og verdimengden Vf = {3, 15, 46}. Vi kan skriva at f (10) = 3 og f (2) = 15.x f(x) 10 3 2 15 5 46 - Ein funksjon kan også vera definert ved ein graf, eller
kurve i xy-planet. Då er
definisjonsmengden tegna horisontalt (i x-retningen) og
verdimengda vertikalt (i y-retningen). For å finna den y
som høyrer til ein bestemt x så startar vi med verdien
på x-aksen. Så går vi vertikalt opp eller ned til vi treff
grafen. Deretter går vi horisontalt (til høgre eller venstre) til
vi treff y-aksen. Sjå nedenfor eit eksempel på dette:
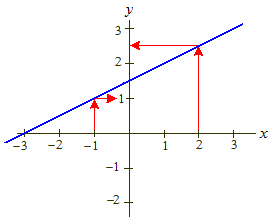
Her er det bare å følja pilene. Hvis vi startar på x = -1 på x-aksen, går opp på grafen, og deretter til høgre på y-aksen, så treff vi y = 1. Hvis vi kallar funksjonen for g så kan vi skriva denne samanhengen som g (-1) = 1. Tilsvarande gir x = 2 at y = 2,5. Dette skriv vi g (2) = 2,5. - Som siste variant vi skal sjå på, er den vanligaste, nemlig når
funksjonen er gitt ved ein formel.
Denne kallar vi for funksjonsuttrykket.
Dette uttrykket bruker vi
då til å rekna ut verdien for kvar x-verdi. Her er eit eksempel:
h (x) = x 2 - 2 x
Her er funksjonen kalla h . Når vi skal finna funksjonsverdien for x = 4, så erstattar vi x med 4 alle stader den fins i funksjonsuttrykket. Då får vi:h (4) = 4 2 - 2 · 4 = 8.
Tilsvarande gir x = 5:h (5) = 5 2 - 2 · 5 = 15.
Når funksjonsuttrykket er gitt kan vi tegna grafen til funksjonen, og omvendt kan vi ofte finna funksjonsuttrykket (om enn kanskje bare tilnærma) ved å studera grafen. Her kan du lesa meir om grafane til ulike funksjonstyper.
Korleis finna definisjonsmengde og verdimengde?
Vi har i utgangspunktet begrensa oss til tal. Nærmare bestemt skal vi sei at x og y må vera reelle tal, dvs. alle tal som vi kan finna på tallinja. (det går an å definera andre tal, såkalte komplekse tal, men det ser vi bort frå i denne diskusjonen.) Spørsmålet er då: korleis bestemmer vi Df og Vf?
Hvis funksjonen er gitt ved ein tabell eller som ein graf, så kan vi identifisera disse mengdene ved å lesa lista (sjå eksempelet over), eller studera grafen. Men hvis den er gitt ved eit uttrykk må du gjera følgande:
- Med mindre oppgaven, eller sunn fornuft tilseier at x er begrensa, så kan du gå ut frå at alle mulige x-verdiar er lovlige, bortsett frå slike som gir ulovlige operasjonar. Eksempel på dette er å dela på 0, eller å ta kvadratrota av negative tal. Ein del andre funksjonar som logaritmen er også begrensa til positive tal.
- Når du kjenner definisjonsmengda, kan du setta inn ulike verdiar frå denne i uttrykket, og derved finna ut verdimengda.
Eksempel: La oss sjå på funksjonen
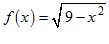 . Vi veit at vi ikkje kan ta kvadratrota av negative
tal. Med andre ord, her må uttrykket under kvadratrota vera større
eller lik 0. Det vil sei at definisjonmengda er bestemt ved ulikheten:
. Vi veit at vi ikkje kan ta kvadratrota av negative
tal. Med andre ord, her må uttrykket under kvadratrota vera større
eller lik 0. Det vil sei at definisjonmengda er bestemt ved ulikheten:
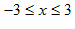 . Hvis vi set inn
ulike verdiar frå definisjonmengda, så ser vi at verdimengda må vera
. Hvis vi set inn
ulike verdiar frå definisjonmengda, så ser vi at verdimengda må vera
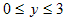 . Her er ein graf som
viser dette:
. Her er ein graf som
viser dette: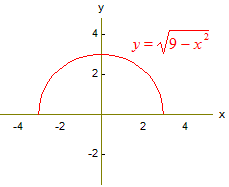
Enkel test om ein graf definerer ein funksjon
Det er ikkje alle kurver i xy-planet som definerer ein funsjon. Definisjonen av ein funksjon seier nemlig at for kvar verdi i definisjonmengda kan vi ha bare ein verdi i verdimengda. Det betyr at grafen til funksjonen ikkje kan sjå slik ut:
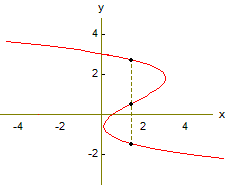
Grunnen er at det fins mange stader der ein x-verdi svarer til fleire ulike y-verdiar. Hvis du kan trekkja ei vertikal linje slik at den skjer grafen fleire stader, så kan den ikkje bli representert ved ein funksjon. I staden seier vi at den gir oss ein relasjon mellom x og y.
No har vi gått gjennom det grunnleggjande: kva som er ein funksjon, og kva som ikkje er ein funksjon. I praksis handlar funksjonar om å kunna tegna grafen, lesa av grafen, eller finna funksjonsuttrykket når grafen, eller to eller fleire punkt på grafen er gitt. Vidare handlar det ofte om å drøfta funksjonar. Det betyr å finna nullpunkt, finna ekstremalpunkt (dvs. toppunkt og bunnpunkt) eller vendepunkt, og det betyr å finna funksjonen sine monotoniegenskaper, dvs. når funksjonen stig og minkar. Her bruker vi som regel den deriverte.
Les meir: omvendte (inverse) funksjonar, funksjonar av fleire variable, vektorfunksjonar og komplekse funksjonar.
