Funksjonar: åtte basistyper

---

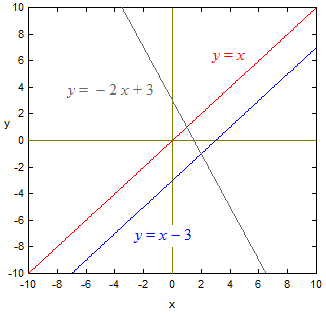
Lineære funksjonar

er funksjonar som kan skrivast på formen:

y = a x + b

der a og b er konstantar. b kallast konstantleddet, og det  fortel kor grafen skjær y-aksen. a kallast stigningstalet, og det fortel kor mykje grafen stig (på y-aksen) når vi forflyttar oss ein enhet til høgre på x-aksen. Grafen til lineærfunksjonen er ei  rett linje. Alle rette linjer kan skrivast på denne formen, men unntakt av vertikale linjer som skrives x = k, der k er ein konstant. Når stigningstalet a er positivt, stig grafen mot høgre, og når stigningstalet er negativt fell den mot høgre. Ei horisontal linje har stigningstal a = 0, og kan dermed skrivast y = b.   Lineære funksjonar er også polynom. Sjå nedanfor.

---

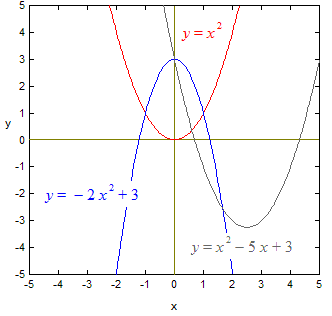
Andregradsfunksjonen

er ein funksjon på formen:

y = a x ²+ b x + c,

der a, b og c er konstantar. Grafen til andregradsfunksjonen kallast for ein parabel. Karakteristisk for grafen er at den har ett (og bare ett) ekstremalpunkt. Dette er eit toppunkt når a er negativ eller eit bunnpunkt når a er positiv. Avhengig av plassering, så kan andregradsfunksjonen ha ingen, ett eller to nullpunkt. Eksempel på anvendelsar er objekt i fritt fall. (kast) .
Andregradsfunksjonar er også polynom. Sjå nedanfor.

Les meir om andregradsfunksjonen.

---

Potensfunksjonen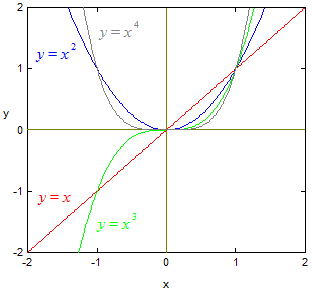

er ein funksjon på formen:

y = a x ^b,

der a og b er konstantar. Dette er ein funksjon som kan ha mange ulike former på grafen, avhengig av kva verdi eksponenten b har. Konstanten a har ikkje så mykje å bety for formen, så i eksempela under antar vi at  a = 1, enkelt og greit. Vi skal sjå på noken tilfeller med ulike b: (merk at ikkje alle variantar er diskutert)

ber eit positivt heiltal.

Det vil sei at funksjonen er x, x², x³, x⁴ osv. Alle disse går gjennom origo, og alle går mot uendelig når x går mot uendelig. Når x går mot minus uendelig så går dei med partalseksponent mot uendelig, mens dei med oddetalseksponent går mot minus uendelig. Sjå grafane til høgre. Merk at sjøl om tredjegradsfunksjonen ofte har både maksimalpunkt og minimalpunkt (sjå polynom nedanfor) , så har x³ det ikkje.

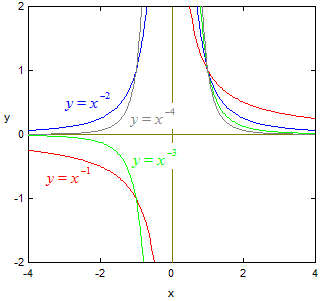
b er eit negativt heiltal.

Dette svarar til funksjonar som x^-1, x^-2, x^-3, x^-4 osv. Sjå grafen til høgre. Disse funksjonane er dermed spesialtilfeller av rasjonale funksjonar, med vertikal asymptote x = 0, og horisontal asymptote y = 0. Sjå nedanfor. For x = 0 har funksjonen ingen verdi sidan dette betyr å dela på null. Når x går mot uendelig, går funksjonen mot null. Dei med odde eksponent er negative for negative x, mens dei med partal eksponent er positive.

b er ein brøk mellom 0 og 1.

Dette er det same som kvadratrot-, tredjerot-, fjerderot-funksjonane. Sjå graf til høgre. Alle disse går gjennom origo. Dei stig bratt til å begynna men vekstfarten minkar heile tida med x. Likevel stig grafen, og funksjonen går mot uendelig når x går mot uendelig.

Les meir om potensfunksjonar.

---

Polynom

er funksjoner på formen:

y = a_n · x ⁿ + a_n −1 · x ^n −1 +  …  + a₂ · x ² + a₁ · x + a₀,

der a_n, a_n −1,  … , a₂, a₁, a₀ er konstantar. Bare heiltallige (positive) eksponentar er tillatt.
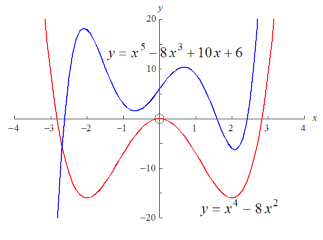
Det vil sei at polynom er ein sum av ledd, der kvart ledd er ein potensfunksjon med heiltallig eksponent. Den største eksponenten kallast graden til polynomet. Til høgre ser vi eit femtegradspolynom og eit fjerdegradspolynom. Jo høgare grad, jo fleire ekstremalpunkt og nullpunkt kan polynomet ha. Eit n-te gradspolynom kan maksimalt ha n -1 ekstremalpunkt og n nullpunkt. Frå og med tredjegradspolynom kan funksjonen også ha eit antal vendepunkt.

Les meir om polynomer.

---

Rasjonale funksjoner

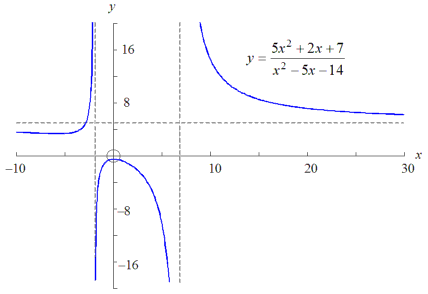
er det same som brøkfunksjonar, dvs. dei er brøker med et polynom i både teljar og nevnar. Når nevnaren er null har funksjonen derfor ingen verdi. Disse x-verdiane representerer vertikale asymptotar. Funksjonen til høgre har to vertikale asymptotar, nemlig  x = −2 og x = 7. Vertikale asymptoter representerer også bruddpunkt. For grafen til funksjonen kan ikkje kryssa eit bruddpunkt. Rasjonale funksjonar er dermed ikkje samanhengande, men er delt i to eller fleire deler. Funksjonen til høgre har td. tre deler.

Hvis polynomet i teljaren og polynomet i nevnaren har samme grad, så går funksjonen mot ein bestemt y-verdi, når x går mot uendelig. Denne verdien er bestemt av forholdet mellom koeffisientane til ledda med høgast grad. Funksjonen til høgre går mot y = 5. Dette representerer ein horisontal asymptote.

Hvis polynomet i nevnaren er av høgare grad enn det i teljaren, så vil den horisontale asymptoten vera y = 0.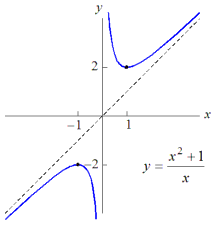

Hvis derimot polynomet i teljaren er av høgare grad enn det i nevnaren, så har funksjonen ingen horisontal asymptote. Den vil då gå mot pluss-minus uendelig når x går mot uendelig. Den kan likevel ha det som kallast ein skrå-asymptote. Funksjonen til høgre nærmar seg linja y = x  for store x.

Merk at formelt så kan ein brøkfunksjon godt ha ein nevnar uten x, dvs at nevnaren bare er ein konstant. Det betyr at formelt er alle polynom også ein rasjonal funksjon. Men disse blir vanligvis ikkje diskutert under denne overskrifta, sidan polynom ikkje har asymptotar.

Les meir om rasjonale funksjonar.

---

Eksponentialfunksjonen

er ein funksjon på formen:

y = a k ^x,

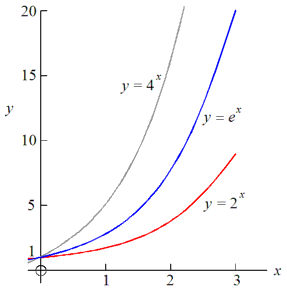
der a og k er konstantar. Merk at her er x i eksponenten, og ikkje i grunntalet slik som potensfunsjonen.  Eksponentiell vekst får vi når noke aukar eller minkar med ein fast prosent over mange periodar. a er startverdien, og k er vekstfaktoren. Vi har at k = 1 pluss minus p/100 der p er prosenten.

Hvis  k er større enn  1 så er resultatet ekspontiell vekst. Eksempel på dette er eit fast beløp som står på konto og får rente og rentesrente, eller ein populasjon (feks. bakterier) som veks med ein fast prosent per år. Som vi ser av grafen så vekst funksjonen fortare og fortare. Dette er ein type vekst som i praksis ikkje kan fortsetta. Les meir om vekst.

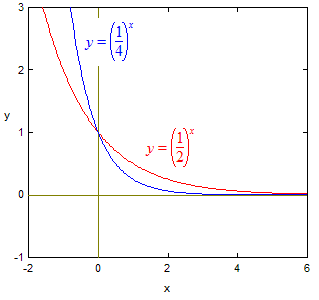
Hvis vekstfaktoren k er mindre enn 1 så har vi eksponentiell nedgang. Grafen startar også då i y = a, men går mot null når x går mot uendelig. Grafen flatar også ut jo større x blir. Sjå figur til høgre.
Eksempel på dette er såkalt radioaktivt sundfall eller decay. For ein radioaktiv isotop vil ein viss prosent av stoffet "forsvinna" (egentlig gå over til eit anna grunnstoff) per sekund.  Eit anna eksempel er korleis sollyset minkar eksponentielt med dybden i sjøen.

Les meir om eksponentialfunksjonen.

---

Logaritmefunksjoner.

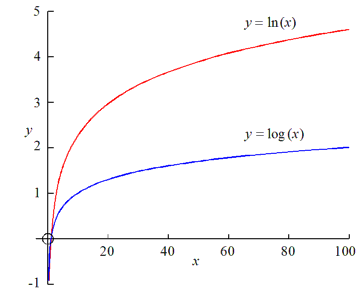
Det fins mange forskjellige logaritmefunsjonar. Den enklaste er

y = lg (x),

Dette er den såkalte tierlogaritmen, sidan den kan definerast som den omvendte funksjonen av 10^x. Vi  kan altså sei at 10^{lg a} = a. Tilsvarande har vi også den naturlige logaritmen, ln(x), som er definert vha. grunntalet e = 2.718281829... e^{ln a} = a. som Disse funksjonane er bare definert for positive x. Formen til grafen er ikkje ulik rotfunksjonane over ved at den heile tida stig, men blir likevel mindre bratt etter kvart. Men til forskjell frå disse, så går ikkje grafen gjennom origo. For små x er funksjonen negativ. Den skjer y-aksen for '  x = 1. Når x nærmar seg 0, så går grafen mot minus uendelig. 

Les meir om logaritmer.

---

Sinusfunksjonen

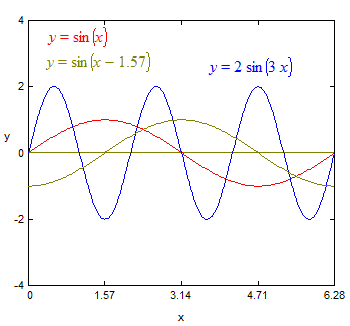
er ein funksjon på formen:

y = a sin (b x + c) + d,

der a, b, c og d er konstantar. Slike funksjonar er nyttige til å beskriva harmoniske bølgeformer (hvis x er avstand) og svingningar (hvis x er tid).  Parameteren d bestemmer likevektslinjen, dvs den verdien bølgen eller svingningen svinger om. a kallast amplituden, og bestemmer kor høgt over likevektslinjen funksjonen er i sine maksimalpunkt.  b bestemmer bredden på bølgeformen, og c bestemmer kor det første nullpunktet befinn seg på x-aksen. Når c = 0 går grafen gjennom origo.

Les meir om Periode, amplitude, likevektslinje og faseforskyvning.