Eulers tal e

Kva er spesielt med talet e, egentlig? Vi veit at det er sånn omtrent 2.718281828..., men kva så? Jo, for det første så antyder prikkane at tallet har uendelig antal siffer etter komma. Men det som ser ut til å vera ein lovmessighet, er det ikkje. Disse siffera "1828", som noken huskar som Ibsens fødselsår, gjentar seg, men det sluttar der (sjøl om det nok kan forekomma lenger ute i rekkja.) Hvis vi tar med 100 siffer så ser det slik ut:

e = 2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274.

Hvis ikkje dette er nok for deg, så kan du finna e med 50 000 siffer her. :) Tallet er produsert av Shigeru Kondo & Alexander J. Yee, som også har funne veldig mange siffer for pi!

Dette talet er eit irrasjonalt tal slik som pi. Det vil sei at det ikkje kan skrivast som ein brøk med heiltal i teljar og nevnar. Og på same måten som pi er viktig i mange samanhengar, er også e det. Talet blir kalla Eulers tall, som etter matematikaren Leonhard Euler, men det var antagelig oppdaga av Jacob Bernoulli i forbindelse med hans arbeid om Compound Interest.

Definisjon

Under har vi tatt med den kanskje mest vanlige definisjonen av e. Det fins mange andre, men dei er likeverdige med denne:

\lim_{n \to \infty} {(1 + \frac{1}{n})}^{n}

Dette betyr grenseverdien av uttrykket (1+1/n) når n går mot uendelig. Med andre ord, vi kan komma så nær e vi vil, bare vi velgjer n stor nok. La oss sjå på noken eksempel:

n	Uttrykk	Svar
10	1.1¹⁰	2.59374246
100	1.01¹⁰⁰	2,704813829
10000	1.0001¹⁰⁰⁰⁰	2.718145927
1000000	1.000001^1000000	2.718280469

Her har vi markert det første sifferet som er feil med rødt. Som vi ser dukkar det opp seinare og seinare ute i desimalane (faktisk like langt ute som antal nullar i n), og det betyr at vi kan rekna ut e med så mange riktige siffer vi vil, bare vi velgjer n tilsvarande stor. Ein heilt annan sak er om dette er den mest optimale måten å rekna det ut på!

Alternativ definisjon

Talet kan også definerast som den uendelige summen

$\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \dots$

Her har vi brukt at feks 3! betyr 1 x 2 x 3 osv. Dette kallar vi fakultet. n! = 1 x 2 x 3 x .... x (n-1) x n.

Andre egenskaper ved e

Kva funksjon er det som blir uendra ved derivering? Med andre ord kva funksjon f(x) er det som passar i likninga* f'(x) = f(x) ? Det viser seg at dette er eksponentiafunksjonen med e som grunntal dvs. f(x) = e^x. f'(x) = f(x) er ein såkalt differensiallikning, som er ei viktig del av anvendt matematikk, og Euler utvikla ein numerisk metode for å løysa slike. Les meir om Eulermetoden og Eulers tal e. Frå eksponentialfunksjonen kan vi også definera den naturlige logaritmen ln, som den omvendte funksjonen til e^x.

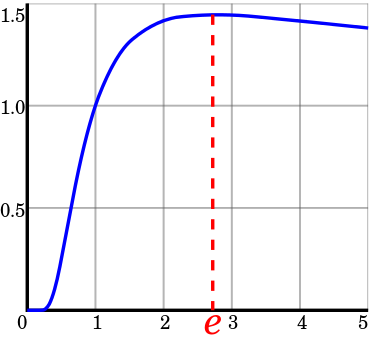
Litt overraskande viser det seg også at e er maksimum av funksjonen x-teroten av x! (eller x^1/x)

Eulers likhet

Som ein kuriositet tar vi med ein likning som har blitt kalla Eulers likhet. Grunnen er at det for mange, i alle fall mange matematikarar, representerer ein av dei vakraste likningane som fins! Den har med både e, π , tala 1 og 0 i ein og same likning. Men det har også med det "mystiske" talet i, som er definert som kvadratroten av -1. Går det an då? Ja, men då må vi utvida den reelle talmengda til å omfatta slike rare tal. Denne mengda kallast komplekse tal. Les meir om talmengder.

$e^{i π} + 1 = 0$

LENKER

e (Euler's Number).
Tallet e.