For å rekna på bevegelser av fysiske objekt, så tar vi ofte utgangspunkt i Newtons lover, og den viktigaste er Fsum = ma. Her er Fsum vektorsummen av alle kreftene som virkar på gjenstanden, m er massen til gjenstanden, og a er akselerasjonen, som også er ein vektor. Hvis vi har rettlinja bevegelse, så blir F og a skalare størrelsar med fortegn i forhold til ein definert pluss-retning, men som regel vil vi ha behov for å kunna både vektorsummar og å dekomponera krefter. Når vi skal finna kraftsummen, må vi vita korleis vi finn alle dei andre kreftene. Så la oss derfor sjå litt på ulike typer krefter som kan dukka opp i ei simulering.
I nesten alle eksempel vi vil komma borti, vil dei objekta vi simulerer vera påvirka av gravitasjonskrafta, dvs tyngdekrafta. Tyngdekrafta er ei tiltrekkjande kraft som er proporsjonal med massane til dei to objekta, og omvendt proporsjonal med kvaratet av avstanden mellom dei. Newtons tredje lov fortel oss at krafta frå ein gjenstand på ein annan er lik krafta frå den andre på den første, men motsatt retta. Så i absoluttverdiar har vi altså at:
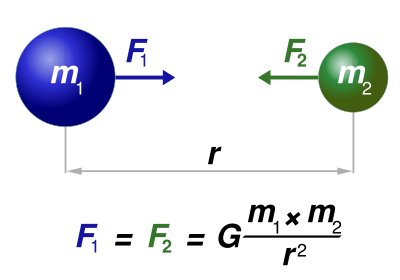
Her er G gravitasjonskonstanten, og har verdien 6,67 × 10−11 Nm²/kg2, og m1 / m2 er massane til dei to objekta.
Avstanden r mellom to punkt finn vi ved å bruka Pytagoras: Her er avstanden lik hypotenusen i ein trekant, der katetane er gitt som differansen mellom punkta sine x- og y- koordinatar. Sidan vi her vil finna r2, så slepp vi å ta kvadratrota, så formelen blir rett og slett:
r2 = (x2 - x1)2 + (y2 - y1)2
Hvis vi modellerer feks. ein satelitt som går i bane rundt jorda, så kan vi ofte lata som om jorda står i ro. Det kjem av at massen til jorda er enormt mykje større enn satelitten sin masse, slik at akselerasjonen blir forsvinnande liten. Hvis ikkje dette er tilfelle, så må vi for kvar iterasjon oppdatera posisjon og fart til alle massane. Sjå Tolegemeproblemet og Trelegemeproblemet.
Hvis vi reknar på bevegelse i tyngdefeltet i lave høgder på jorda, eller andre planeter, så kan vi med god tilnærming setja at tyngden til ein gjenstand er konstant. Sjå Bevegelse med konstant akselerasjon. Då set vi at G = mg, der g er tyngdeakselerasjonen (konstant) For mange formål er det nok å setja g = 9,81 (eller kanskje til og med 10 hvis du ikkje treng å vera så presis). På Månen er g lik 1.62 m/s2. Sjå tabell for verdiane på andre planeter.
Vi tar med to variantar av den elektrostatiske krafta, fordi disse er veldig like på tyngdekrafta, og algoritmane tilsvarande like. Det vi må passa på er fortegna og verdiane på konstantane.
Krafta mellom to elektriske ladningar q1 og q2 er gitt som
Her er ke Coulombs konstant og er lik 8.987742438 * 109 N m2 C-2
Formen til denne lova er akkurat som gravitasjonslova, bare at vi har ein annan konstant, og vi har erstatta massane med dei elektriske ladningane q1 og q2. Disse har enhet Coulomb (C), og kan ha både positiv og negativ verdi. Krafta mellom to like ladningar (+ og + eller - og - ) virkar fråstøytande, mens når vi har ein positiv og ein negativ ladning, så virkar krafta tiltrekkjande (som tyngdekrafta)
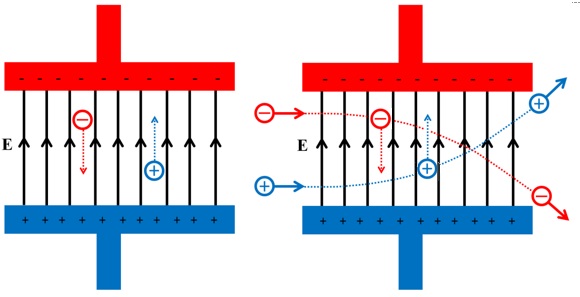
På same måten som gravitasjonskrafta får ein enklare form nær jordoverflata der g er tilnærma konstant, så får vi ein enklare variant av den elektriske krafta når det elektriske feltet er konstant. Mellom to ladde plater vil det vera ein tilnærma konstant elektrisk felt E, som går frå den positive plata til den negative. Ein ladd partikkel som befinn seg mellom platene vil då oppleva ei elektrisk kraft gitt ved F = qE. Når partikkelen har negativ ladning vil krafta virka motsatt av feltretningen, dvs mot den positive plata, og omvendt. Sjå figuren nedanfor.
Vi bruker engelsk notasjon. Luftmotstand heiter "drag" på engelsk, så vi bruker derfor ofte suffikset "D". For dei fleste formål gjeld det at motstandskrafta FD er proporsjonal med kvadratet av farten til gjenstanden, dvs:
FD = -k * v2
Retningen til luftmotstanden er motsatt retta av farten. Verdien av konstanten k, er avhengig av både størrelsen til objektet, formen og overflata. I tillegg er også ulike parameterar for lufta / væska viktige. For å finna verdien til k, kan du lesa meir om luftmotstand.
Ei fjør er omtrent beskriven av ein Hookes lov: F = kx, som seier at den krafta du treng for å strekkja ei fjør er proporsjonal med lengden du strekk den x. Retningen til fjørkrafta er langs fjøra i retning mot likevektspunktet. Dette kan vi bruka til å simulera eit elastisk svingesystem. Les meir om svingesystem.
Oppdriften til ein gjenstand som er heilt eller delvis nedsenka i ein gass eller ei væske, er gitt ved Arkimedes lov. Den seier at oppdrifta er lik vekta av den fortrengte væskemengda. Hvis ein gjenstand flyt i vatn (ingen bevegelse i y-retning), så må oppdrifta vera lik tyngda av den vannmengda som gjenstanden fortrenger, med andre ord, den vannmengda som ville ha vore der hvis ikkje gjenstanden tok opp plassen. Dette er markert med gult på figuren under. Merk at oppdrifta O då er lik vekta av ei vannmengde med volumet V. Vekta er lik mg, der massen til vatnet kan finnast som tettheten ρv til vatnet * V. Altså kan vi skriva at O = ρv V g
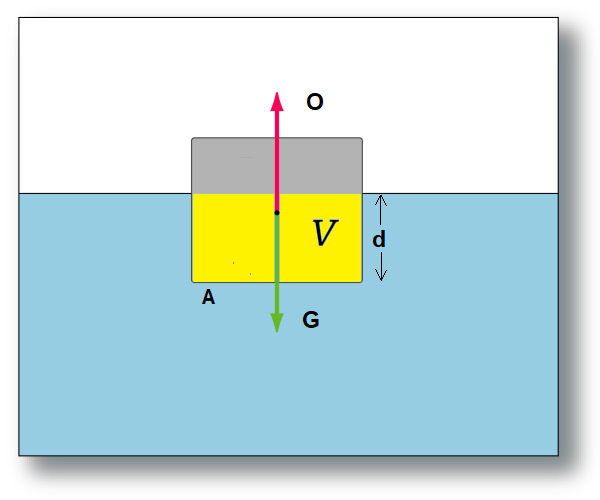
Tettheten ρv til vatn kan vi ofte setja som 1 kg per liter. (varierer med temperatur og saltinnhald) Is har litt mindre tetthet og vil derfor flyta, mens gjenstandar som har større tetthet enn vatn vil synka. Ein båt som blir lasta full, får større vekt, og vil derfor liggja lavare i vatnet for å halda seg flytande. Då vil V bli større, og dermed også oppdriften.
Eit flytande objekt som blir pressa ned i vatnet vil fortrenga meir væske (V blir større) Oppdriften blir derfor større enn tyngda, og objektet vil stiga oppover. Tilsvarande, hvis det blir heva over likevektspunktet vil det synka ned. Ein gjenstand vil dermed kunna svinga om likevektspunktet på same måten som ein elastisk pendel. Men sidan vatn har stor motstand, så vil ein slik svingning fort bli dempa.