
Trelegemeproblemet er eit problem innan himmelmekanikken (også kalt celest mekanikk) som går ut på å bestemma banane for tre objekt som beveger seg under gjensidig gravitasjonspåvirkning. Trelegemeproblemet kan bare løysast analytisk i spesialtilfeller, og vi må derfor ty til simuleringar for å finna banane. Når ein kjører ein simulering med tre objekter med tilfeldig startfart og posisjon, vil ein ofte få noke i retning av dette :

Animasjonen over (laga av R. Moeckel.) er bare ein kort del av ein simulering der vi ikkje kjenner fortsettelsen. Det kan henda at dei tre objekta vil fortsetja i kaotiske banar nær kvarandre, men det kan også henda at to av dei kræsjar i kvarandre, eller at det eine objektet får så mykje energi frå dei to andre at det stikk av. Men det fins også mange løysingar med (meir eller mindre) periodiske banar som vi skal sjå nedanfor.
Mange av vitskapens klokaste hodene har studert trelegemeproblemet, blandt disse Lenonhard Euler og Joseph-Louis Lagrange.
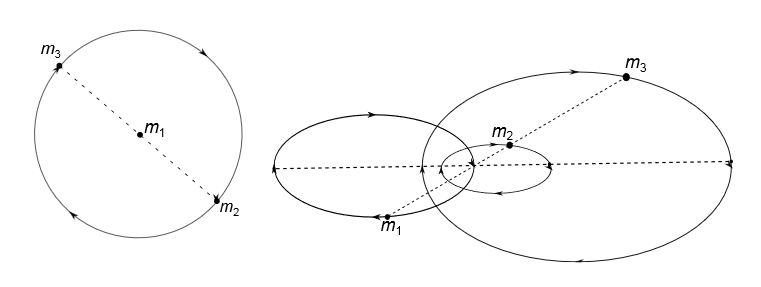
Her ligg dei tre objekta alltid på linje. Hvis m2 er lik m3, og med passande startfart, så får vi den sirkulære løysinga til venstre. Hvis ikkje får vi løysinga til høgre. Men eit slikt system vil vera ustabilt, og derfor kan vi ikkje forventa å finna det i verkeligheten. Det er blitt framlagt ein hypotese om at jorda har ei slags "motjord" på motsatt side av sola. Som vi forstår, er dette teoretisk mulig. Ei slik jord ville ikkje vore synlig frå jorda, og derfor er dette ganske beleilig for tilhengarane. Men vi hadde jo oppdaga den på andre måtar likevel, så den må dei litt lenger ut på landet med. Men dette er ikkje det same som å sei at ei niande planet ikkje eksisterer.
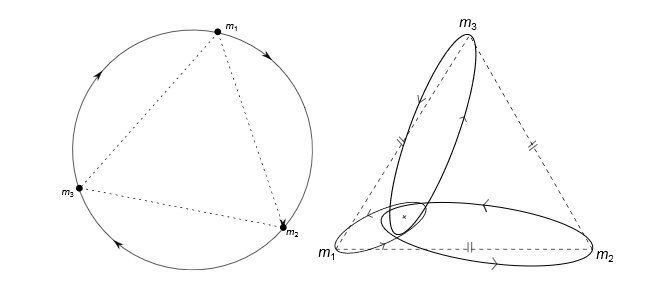
I 1772 oppdaga Lagrange ei anna løysing der dei tre objekta alltid dannar ein likesida trekant. Til venstre ser vil eit spesialtilfelle der dei tre massane er like. I midten og til høgre ser vi korleis det ser ut med ulike massar. Lagrange-løysinga er heller ikkje stabile generelt. Men når den eine av objekta er ei sol, det andre ei stor planet, og det siste ein mindre asteroide, så kan denne liggja i eit av fem såkalte Lagrangepunkt.
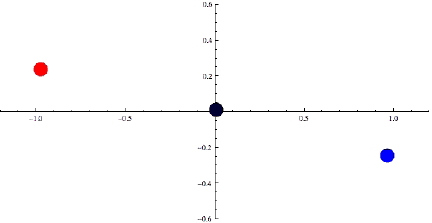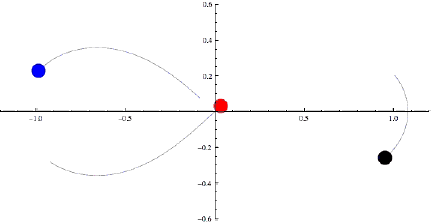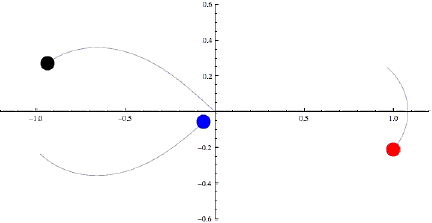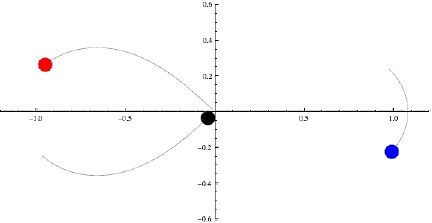
Åttetalet er eksempel på det som blir kalla ein koreografi. Dette er banar der vi har eit antal objekt med lik masse som går i same bane. Eit anna eksempel med tre objekt er dette:
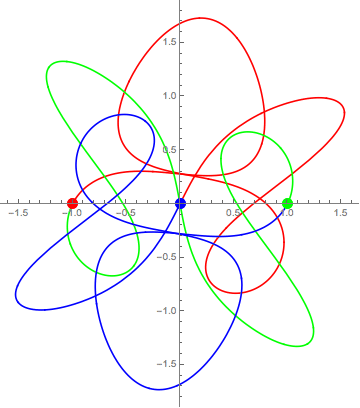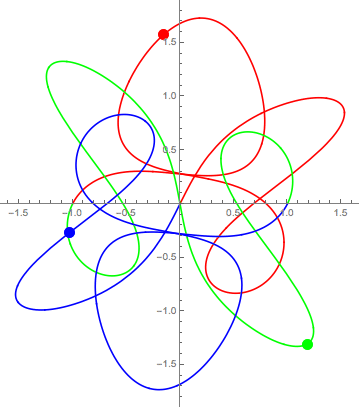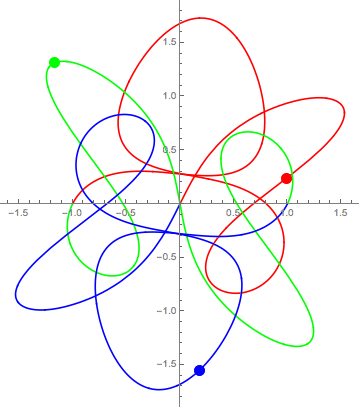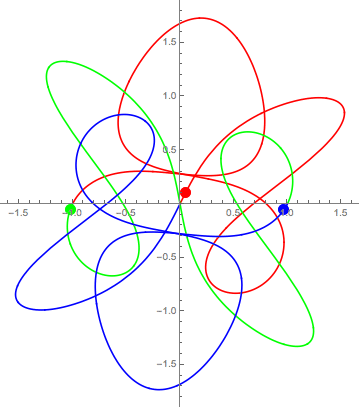
Her kan du test manga andre koreografiar.
For fleire eksempel på periodiske løysingar, sjå videoen 3 Body Problem - Periodic Solutions.
Som sagt, sjøl om mange andre løysingar er teoretisk mulige, vil dei vera
ustabile. I verkeligheten vil vi derfor med tre objekt ofte observera noke
i retning eksempelet over. Eit spesialtilfelle av dette er når den
raude massen er mykje større enn dei to andre, slik stjerna i sentrum av
eit solsystem er. Då vil ha det som vi kan kalla "Sol og planeter" -konfigurasjon.
Ein annan vanlig, og stabil konfigurasjon er ein konfigurasjon med "sol-planet-måne".
Her har vi også eit objekt som er mykje tyngre enn dei to andre, og det
andre og tredje objektet er i bane rundt kvarandre.
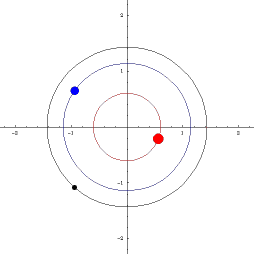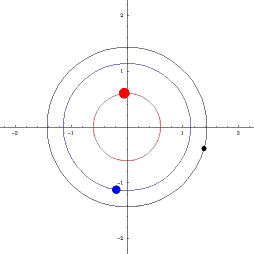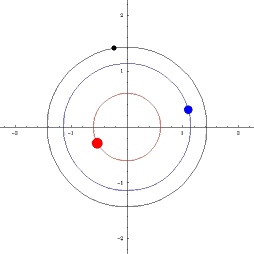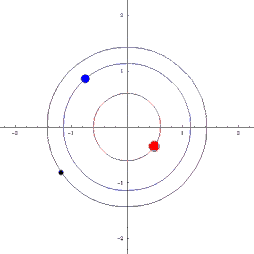
Ein tredje muligheten er med to tunge objekt som går i ein bane nær
kvarandre, og med et tredje lenger ute, som då vil gå i bane rundt begge.
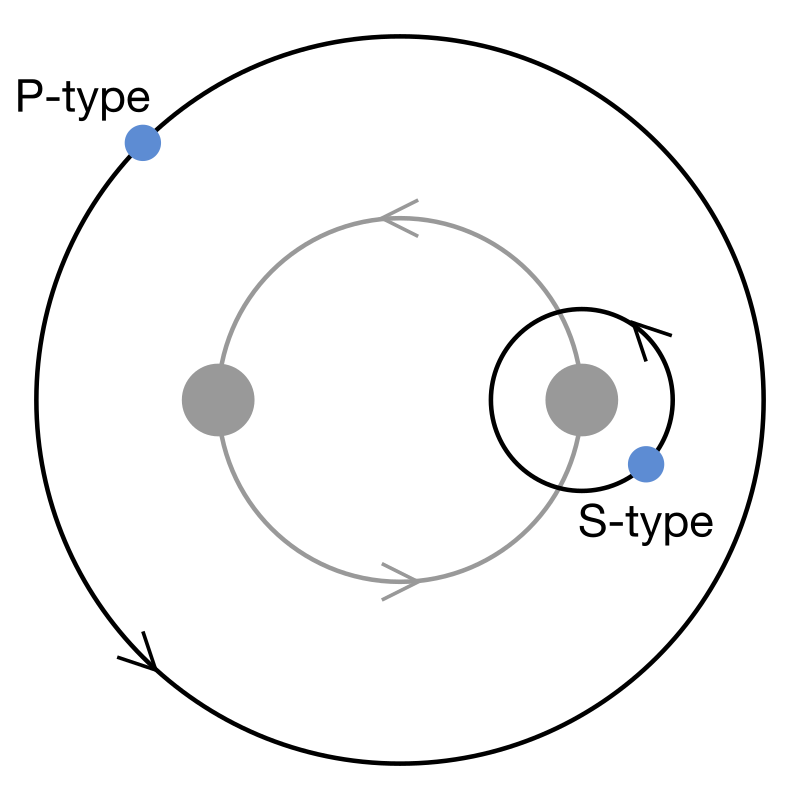
Dette er den såkalte P-type banen til planeter i bane rundt
dobbeltstjerner. Sjå figuren under.
Planeter som bare kretsar rundt den eine av to dobbeltstjerne, seiest å ha ein såkalt "S-type"-bane, mens dei som kretsar rundt begge, seiest å ha ein "P-type"-bane.
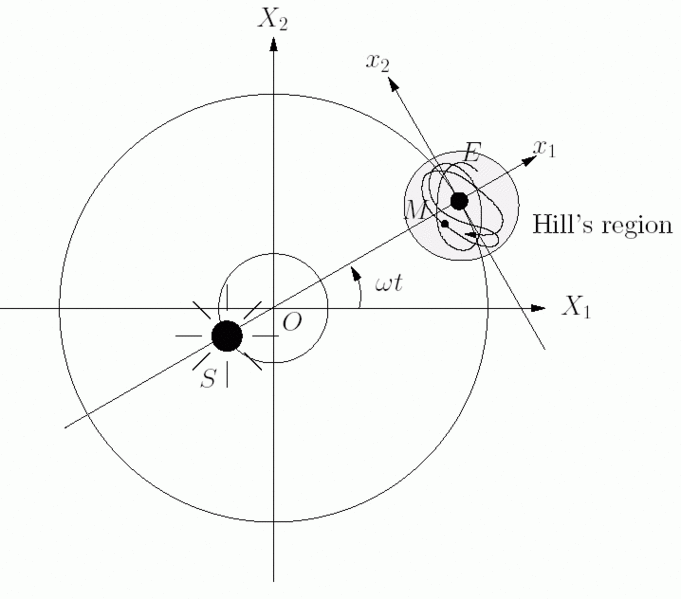
Objekt som er små nok i forhold til ei planet, kan gå i bane rundt denne, og bli ein måne.Vår måne har en stabil bane rundt jorda i ein avstand av 384 400 km. Dette er godt innanfor det som kallast Hill-sfæren som er det området der jorda sin gravitasjon dominerer over sola sin. Jorda sin Hill-sfære er på ca. 1.5 millionar km, og er bestemt både av massane til jorda og sola, og av jordbanen. Hvis jorda hadde vore lettare, så hadde Hill-sfæren vore mindre, og jorda ville ikkje klart å halda på månen, som då ville gått i ein uavhengig bane rundt sola. I teorien kan også månen ha ein måne, men den vil ikkje vera stabil pågrunna av tidevannskreftene,
Objekt som ligg på grensa mellom sola og planeten sine dominansområder kan enda opp med å veksla mellom disse to, slik animasjonen under viser:
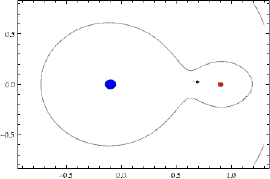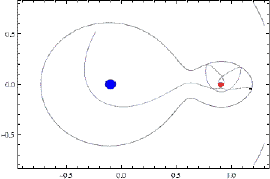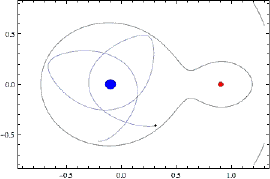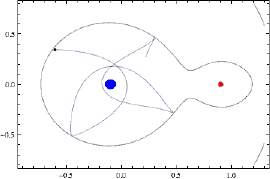
Under dei rette omstendigheter kan ei planet fanga inn eit objekt som blir ein ny måne. (Ein slik blir kallas for ein irregulær måne, til forskjell frå regulære månar som er danna i banen sin) For at dette skal skje må objektet tapa energi, og dette kan skje gjennom påvirkning frå andre planeter eller objekt. Noken gonger har objektet akkurat nok energi til å riva seg laus igjen. Det kan då "kretsa" rundt planeten i ein komplisert bane, før det drar vidare. Jorda har hatt mange slike besøk opp gjennom tidene. For eksempel var asteroiden 2006 RH120 fanga av jorda frå september 2006 til juni 2007.
Eit eksotisk eksempel på korleis tre objekt kan oppføra seg er dei to månane til Saturn, Epimetheus og Janus, som går i nesten same bane. Dette kallast ko-orbitale månar. Men det spesielle med disse to stoppar ikkje der, for dei har nemlig motsatt rotasjon om Saturn. Det medfører at dei møtest. Men i staden for å kollidera tar dei ein sving rundt kvarandre og retunerer i motsatt retning, slik figuren under viser:
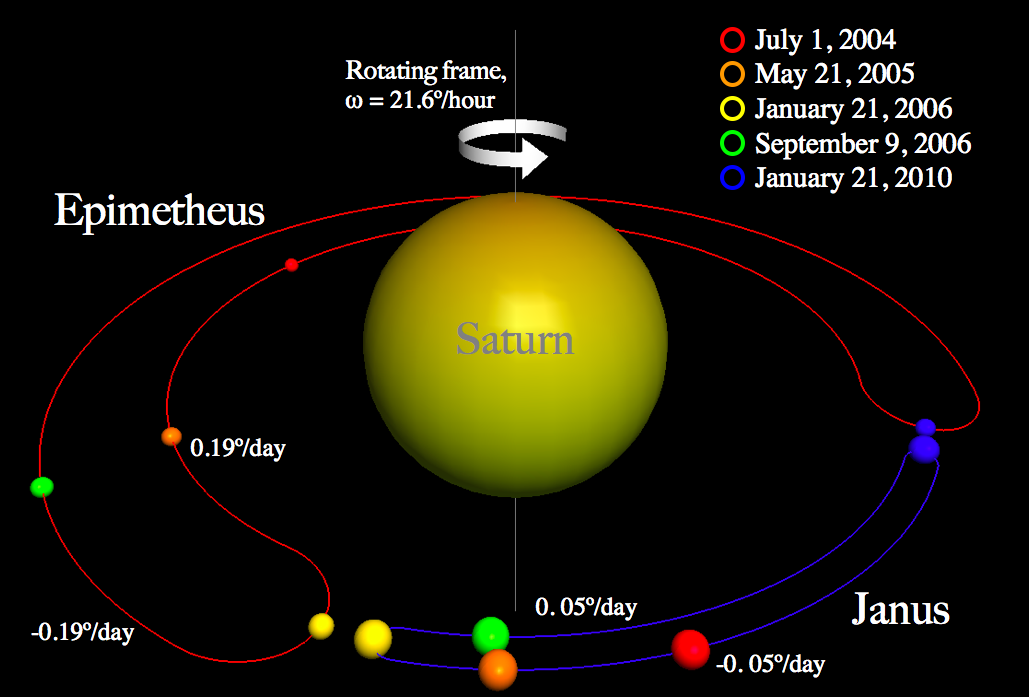
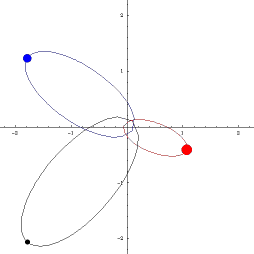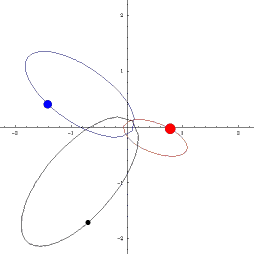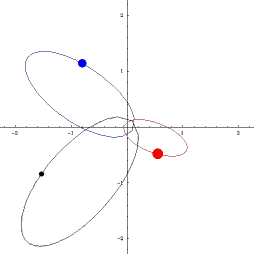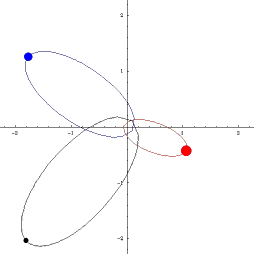
Det fins astereoider som er i 1:1 resonans med jorda. Det betyr at dei har same omløpstid som jorda, men dei deler ikkje bane, og dei går heller ikkje i bane rundt jorda. Slike asteroidar kallast for kvasisatelittar. Ein av disse er Cruithne som er vist i figuren under. Den raude banen er jordbanen. Den blå banen er Cruithne sin bane, og den gule er slik den er, sett frå jorda.
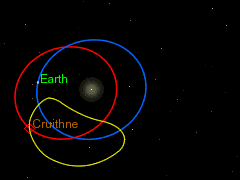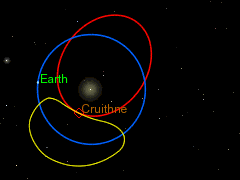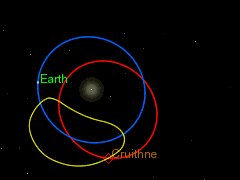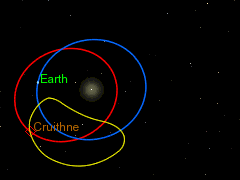
Banar som den til Cruithne er ikkje stabile. Datamodellar indikerer at Cruithne vil tilbringa bare omkring 5000 år i den noverande banen. Så kan det henda at det vil gå inn i ein ekte bane rundt jorda, og då vil den altså bli ein måne nr to. Men etter omkring 3000 år til, så vil den sleppa unna og gå tilbake til ein bane rundt sola.
Three Body Problem (Scholarpedia)
Ducati Stable Solution to the Planar Three-Body Problem.
Super Planet Crash. Try to Build a Stable Solar System: Orbital Physics and World Making.