Tvilling-paradokset
Dette er eit berømt "paradoks" som har generert mykje diskusjon opp igjennom åra, sjølv om fysikarar stort sett er enige om at det ikkje er noko paradoks.
Vi kan ta utgangspunkt i tvillingane Arve Tellusen og Bella Stella, også kalla A og B. A sit heime på jorda (og øver filolin), mens B er på ein intergalaktisk chartertur (med Star-tour) og reiser i et romskip med oppunder lysets hastighet for så å reisa tilbake igjen. I følge den spesielle relativitetsteorien går tida saktare i kvilesystemet (dvs romskipet) enn i et system som har ein hastighet i forhold til kvilesystemet. Sagt med andre ord: tida går saktare i romskipet enn på jorda. . Dette kan vi utttrykkja ved likninga
t = γ t0 der γ er Lorentzfaktoren, som er gitt ved
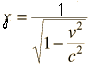
Paradokset oppstår i det vi tenkjer oss reisa sett (og målt) frå romskipet. I romskipet sitt system er det B som er i ro og jorda, dvs. A, som reiser av gårde i stor fart. Med andre ord: sett frå B sitt system vil tida på jorda gå saktare enn på romskipet, og B vil derfor ha blitt eldre enn A. At begge ser at den andre blir eldre er riktig når vi ser isolert på einveis-tur. Men begge klokkene kan ikkja ha gått saktare enn den andre når Bella har returnert til jorda. Det ville ha vore eit reelt paradoks.
Den enkle forklaringen på dette er at det som i utgangspunktet ser ut som symmetrisk problem ikkje er det. A, som er i ro, ER i et treghetssystem (eit system der mekanikkens lover gjeld) mens B som jo først må akselerera romskipet og deretter bremsa ned, snu og gjenta dette på tilbaketuren, er IKKJE i et treghetssystem. (Vi ser her bort frå jordens gravitasjonsfelt som medfører at jordsystemet heller ikkje er eit skikkelig treghetssystem) At B er akselerert kan vi jo observera direkte: Vi ser at ho fyrer av rakettmotorane og ho kan føla akselerasjonen. Den spesielle relativitetsteorien (SR) seier ikkje at alle referansesystem er likeverdige, bare dei som er treghetssystem. SR foretrekk jordsystemet, og dermed det første svaret: A er eldre enn B ved tilbakekomst.
Dopplerskift-forklaringa
Det er mange andre måtar å forklara dette på. Den eine kan kallast Dopplerskift-forklaringa
La oss sjå på hendelsane i litt meir detalj. Vi kan forenkla problemet litt ved seia at B bare passerer jorda til og frå, og dermed kvitta oss med B sin akselerasjon i starten og på slutten av turen. Vi forkuserer på det som tvillingane kan sjå med sine egne auger. Vi utstyrer Arve og Bella med klokker som sender ut eit lysglimt kvart sekund og utrulig sterke teleskop, slik at begge kan sjå den andre si klokke.
Start: Bella suser forbi Arve og dei synkroniserer klokkene til
0.
Utreise: La oss seia at Bella reiser avgårde i eit år i nesten 99
prosent av lysfarten. La oss sei at farten er slik at gamma er akkurat 7,
dvs. at turen tar 7 år sett frå jorda.
Sving: Bella fyrer motorane i ein dag (i jordsystemet) før ho
reiser tilbake til jorda i samme fart som utreisa.
Tilbakereise: Bella reiser tilbake i 1 år i 99 prosent av
lyshastighet.
Slutt: Bella raser forbi Arve i den andre retningen og dei
samanliknar klokkene sine.
I følge A har det no gått to 14 år og ein dag, mens Bella si klokke bare viser litt over to år. (Det viser seg at hvis nedbremsinga og akselerasjonen var jevn, ville svingen ta litt over 15 timar for Bella)
Du trur kanskje no at Arve ser at klokka til Bella blinkar kvart sjuande sekund, men det er feil! Han vil rekna ut dette, men det er ikkje det han ser, for det er to ulike effektar ute og går her: Den første er den relativistiske tidsforlengelsen som gitt ved likninga over. Den andre er ein forsinkelse som kjem av at kvart påfølgande lysblink har stadig lengre vei å reisa sidan Bella er på vei bort. For å finna det rette svaret kan vi bruka den relativistiske Doppler-formelen som tar hensyn til begge effektane, og då finn vi at A ser ein blinkfrekvens på omtrent eit blink per 14 sek på utreisa, altså at klokka til Bella går for seint. Tilsvarande gir Doppler-formelen på heimreisa at han ser 14 blink per sekund, altså at Stella si klokke går for fort! Bella ser akkurat det same.
Så lang er det greit, men denne diskusjonen ser ut til å bare tydeliggjera paradokset: Bella ser det Arve ser, nemlig ei sakte klokke på utreise og ei fort klokke på heimreise. Kor kjem då asymmetrien frå? Svar: i lengda av utreisa og tilbakereisa slik dei blir sett. For Bella tar begge etappane omtrent et år. I A sitt system er det slik at Bella snur i år 7 i ein avstand av nesten 7 lysår, så han vil ikkje sjå svingen før nesten i år 14. Arve ser altså ei lang utreise og ei veldig kort tilbakereise.
Bella ser at Arve blir sakte eldre på utreise, men mykje fortare eldre på heimreise, og for henne er det den siste effekten som er størst, dvs i netto har han blitt mykje eldre enn henne. Arve ser også at Bella blir langsom eldre på utreise, og veldig fort eldre på heimturen, men sidan heimturen tar mykje kortare tid er det den første effekt som er størst her, dvs. i netto ser han at Bella ikkje har blitt så gammal som han. Dei er altså enige om denne konklusjonen, og paradokset er forsvunne.
Andre forklaringar
Det vert hevda at ein bare kan løysa tvillingparadokset ved hjelp av den generelle relativitetsteorien, men som vi ser bruker denne forklaringsmodellen bare den spesielle relativitetsteorien, og det ser ut til å virka OK. Poenget er at det lar seg gjera å beskriva akselerasjon vha SR, så lenge du måler den frå eit system som ikkje er akselerert, det vil seia akkurat slik klassisk mekanikk behandlar akselerasjon frå et treghetssystem. Likevel kan andre forklaringar, kasta meir lys over problemet.
