Talmengder
Ei mengde er ein samling av ulike objekt. Vi er som regel opptatt av tallmengder. For eksempel kan vi definera ei mengde M som består av tala 1, 3 og 5. Dette er ei endelig mengde som vi kan skriva som
M = {1, 3, 5}.
Når vi skriv opp alle tala på denne måten med klammeparenteser, seier vi at mengden er på listeform. For å indikera at eit tal x er med i mengda skriv vi x ∈ M (x er element i M)
Den tomme mengden: Hvis ei mengde ikkje inneheld noken element,
kallar vi det for den tomme mengden. Denne har fått symbolet 

Delmengder: Hvis vi ser på mengden D = {1,3}, så ser vi at alle tala som er med i D også er med i M, men motsatt fins det tal i M som ikkje med i D. Då seier vi at D er ei ekte delmengde av M. Dette skriv vi som: D ⊂ M. Eit litt svakare krav er hvis vi har ei mengde E der vi kan skriva E ⊆ M. Det vi veit om mengda E då, er at den enten er ei ekte delmengde av M, eller at den er lik M.
Operatorane (Kva kan vi "gjera" med mengder?)
Hvis A = {1, 3, 5} og B = {4, 5, 6} så bruker vi som regel* disse tre måtane å kombinera disse på, nemlig union, snitt og mengdedifferanse:
- Unionen av A og B er definert som alle element som er med i A eller B. Vi skriv dette som A ∪ B. Vi har altså at A ∪ B = {1, 3, 4, 5, 6}.
- Snittet av to A og B er definert som alle element som er med i både A og B. Vi skriv dette som A ∩ B. Vi får at A ∩ B = {5} fordi det bare er 5 som er med i begge mengdene.
- Mengdedifferansen (eller Komplement) av to A og B skriv vi A \ B. Dette er mengden av alle element som er med i A, men ikkje i B. Vi får A \ B = {1, 3}.
Venn-diagram
Mange gonger er det lurt å tegna mengdene. Då kan vi bruka såkalte Venn-diagram der kvar mengde er representert med ein sirkel. Nedanfor har vi tegna to mengder A og B som overlappar. Unionen representerer då alle elementa i begge mengdene, og er tegna til venstre. Snittet er det som er felles i begge mengdene, mao. "overlappet". Til høgre er mengdedifferansen B \ A. (Hvis vi tenkjer oss A til venstre)
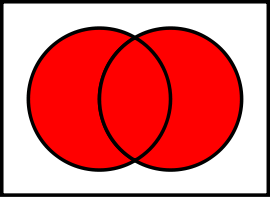
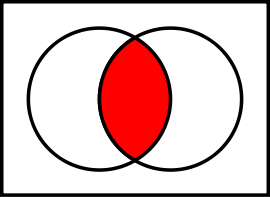
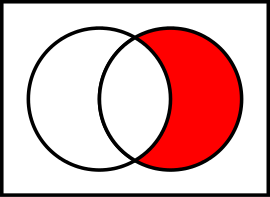
Vanlige talmengder
Det er vanlig å dela tala inn i følgande kategoriar:
- Naturlige tal. Dette er dei tala vi brukar til å telja med:
= {1, 2, 3, 4, 5 ...} (Merk at noken gonger er 0 tatt med her.)




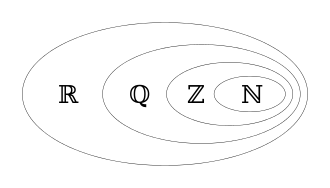 delmengde av
delmengde av 





Vi kan oppsummera samanhengen mellom dei ulike typane med Venndiagrammet til høgre:



For dei som lurer på bokstavane som vi bruker: Z skal komma frå det tyske
ordet for tal: "zahlen", og Q kjem visstnok frå det italienske#
ordet for kvotient: "quoziente." C kjem rimeligvis frå engelsk "complex".
Tal som er med i 





Intervall
Men la oss venda tilbake til tallinja. Ofte har vi bruk for å beskriva ein del av tallinja. For eksempel alle tal x som er slik at 2 < x < 5, altså alle tal som er større enn 2 og mindre enn 5. Disse kan vi skriva som intervallet <2,5>. Dette kallast for eit åpent intervall, sidan grenseverdiane 2 og 5 ikkje er med i mengden. Hvis vi tar dei med, så får vi eit lukka intervall: Hvis 2≤x≤5 er mengden av alle tall som er større eller lik 2 og mindre eller lik 5. Dette skriv vi som [2,5]. Hvis det eine endepunktet er med, men ikkje det andre, kallast det for eit halvåpent intervall, feks. [2,5>. Alle disse intervalla erendelige intervall. Men vi har også bruk for å beskriva intervall som går mot uendelig i eine eller andre retningen. Tal som er større eller lik sju, kan vi skriva som [7,∞>
Vi har også ofte behov for å skriva mengder som er sett saman av to eller fleire intervall. Tal som er mellom 2 og 5 eller større enn sju kan vi då skriva som unionen av to intervall: <2,5> U <7,∞>
Kardinaltal.
Antal element i ei mengde kallast for kardinaltalet. Mengden A = {2, 4, 6} inneheld 3 element, og har derfor kardinalitet 3. Kva så med uendelige mengder? Det viser seg at det er forskjellige former for uendelighet, og det gir derfor meining å operarera med ulike kardinaltal for dei relle tala enn for for eksempel dei naturlige tala. Dette har med begrepet tellbarhet å gjera: dei naturlige tala er tellbare, mens dei reelle er det ikkje.
NOTER
* Det fins også andre operasjon som feks. det kartesiske produktet.
# Det skal vera italienaren Giuseppe
Peano som introduserte bokstaven Q for rasjonale tal.
