oyro.no - LIVET, UNIVERSET OG ALT MULIG

Sannsynlighet

Grunnleggande begrep

Tilfeldig forsøk: Å kasta kron og mynt er et eksempel på et tilfeldig forsøk eller bare et forsøk. I et tilfeldig forsøk er resultatet ukjent. Vi kjenner bare dei mulige utfalla.
Utfall og utfallsrom: For mynt og kron har vi bare to mulige utfall, nemlig kron (K) eller mynt (M). Mengden av alle utfall kallar vi utfallsrommet til forsøket, og er ofte betegna med bokstavenU. I vårt forsøk kan vi altså skriva U = {K, M}
Hendelse: Ein hendelse definerer vi som eit eller fleire utfall. Eit enkelt terningkast har utfallsrommet U = {1,2,3,4,5,6}. Då kan vi definera hendelsen A: terningen viser eit oddetal. Den vil bestå av utfalla 1, 3 og 5. Vi skriv: A = {1,3,5}.
Den motsatte (komplementære) hendelsen: Når vi, eller oppgaven, har definert ein hendelse A, så kallar vi alle dei andre utfalla som den komplementære eller motsatte hendelsen. Vi skriv ofte A for denne hendelsen. For eksempelet vårt er det at terningen viser eit partal, altså, A = {2,4,6}

Dei store talls lov, og begrepet sannsynlighet

Eit mål for kor ofte vi får kron eller mynt, er den relative frekvensen. Hvis vi kastar mynt og kron 50 gonger og får mynt 22 gonger, så er den relative frekvensen for mynt lik 22 /50 = 0,44. Hadde vi kasta pengestykket mange nok ganger, ville den relative frekvensen ha nærma seg eit bestemt tal, som vi trur er 0,50. Hvis vi gjentar et forsøk mange nok gonger, vil den relative frekvensen for et utfall nærma seg ein bestemt verdi.Denne verdien er sannsynligheten for utfallet.
Det er vanlig å bruka bokstaven P for sannsynlighet. Bokstaven P står for probability, som er det engelske ordet for sannsynlighet.P(M) er ein kortfatta skrivemåte for sannsynligheten for å få utfallet mynt ved kast av et pengestykke. For ein nornal mynt vil vi anta at P(M) = 0,5

For sannsynlighet gjeld alltid:

Sannsynligheten for eit enkelt utfall er eit tal mellom 0 og 1(0 % og 100 %).
Sannsynligheten for alle utfalla til saman er lik 1(100 %).
Sannsynligheten for ein hendelse er lik summen av sannsynlighetane for dei utfalla som inngår i hendelsen.
Sidan summen av alle sannsynligheter er lik 1, får vi då regelen P( A) = 1 - P(A)

Sannsynlighetsmodellar

Ein oversikt over alle utfall og sannsynlighetane til dei enkelte utfalla i eit forsøk kallar vi for ein sannsynlighetsmodell.
Tabellen viser ein sannsynlighetsmodell for kast med ein terning:

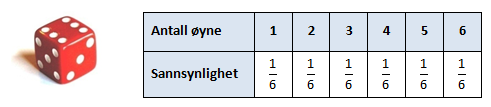
I denne sannsynlighetsmodellen er alle sannsynlighetene for utfalla like store. Vi seier då at sannsynlighetsmodellen er uniform. Eit eksempel på ein sannsynlighetsmodell som ikkje er uniform, er modellen for blodtypen til ein blodgivar. Her er sannsynlighetane for dei enkelte utfalla ikkje like store:

Blodtype	0	A	B	AB
Sannsynlighet	0,40	0,48	0,08	0,04

Vi legg merke til at i begge modellane over er summen av sannsynlighetane lik 1, slik det må vera for ein gyldig modell.

Reglar for uniforme modellar

Enten modellen er uniform eller ikkje, kan vi finna sannsynligheten for ein hendelse ved å summera enkeltsannsynligheter. Sannsynligheten for å ha blodtype 0 eller A er for eksempel då lik 0,40 + 0,48 = 0,88. Men for uniforme sannsynlighetsmodellar har vi i tillegg disse to reglane:

P(et utfall) = 1/antall mulige utfall
P(A) = antall gunstige utfall for A/ antall mulige utfall

Begrepet "gunstige utfall" er det samme som "utfall som er med i hendelsen". Sidan det er tre gunstige utfall for hendelsen "oddetall i et terningkast", så blir sannsynligheten for denne lik 3/6 = 1/2.
Når vi skal finna antall mulige utfall kan vi ofte bruka multiplikasjonsprinsippet. For eksempel blir antallet mulige utfall ved kast av to terningar lik 6 x 6 = 36, fordi første kast har 6 muligheter og andre det same. Sjå meir om dette nedanfor.

Mengder

Ei mengde er ein samling objekter, til vanlig kalla element, men som i vår samanheng som regel er det samme som utfall. Vi kan då sei at ei mengde representerer ein hendelse. Hvis A = {1,3,5}og B = {4,5,6} så er det to måtar å kombinera disse på som er viktige i forhold til sannsynlighet, nemlig union og snitt:

Unionen av to mengder A og B er definert som alle element som er med i A eller B*. Vi skriv dette som A ∪ B. For mengdene over har vi altså at A ∪ B = {1,3,4,5,6}, mao. alle utfall bortsett frå 2 som hverken er med i A eller B.
Snittet av to mengder A og B er definert som alle element som er med i både A og B. Vi skriv dette som A ∩ B. For mengdene over har vi at A ∩ B = {5} fordi det bare er 5 som er med i begge mengdene.

* NB! Når ein td. skriv "enten ski eller fotball" så betyr det at dei som driv med begger deler er utelatt. Det er altså ordet "enten" som fortel oss dette. Men hvis det bare står "ski eller fotball", så ville det betydd at dei som driv med begge deler var inkludert. Så i eksempelet over må altså vi ta med 5.
Du kan lesa meir om mengder på Store Norske Leksikon eller Wikipedia

Venndiagram

Ein vanlig måte å tegna mengder på er ved hjelp av såkalte Venndiagram. Kvar mengde blir representert ved ein sirkel (eller lignande). Vi kan då tegna unionen av to mengder A ∪ B slik:

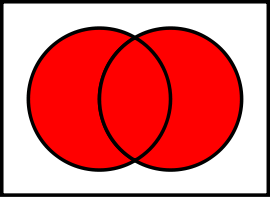
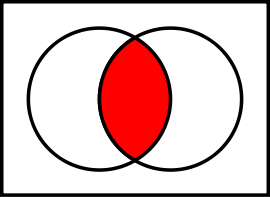
Snittet A ∩ B kan tegnast slik:

Addisjonssetningen

Når vi veit at sannsynligheten for ein hendelse er lik summen av sannsynlighetane for dei utfalla som inngår i hendelsen, så er det fristande å gjera det same for unionen av to hendelsar, dvs å summera sannsynligheten for dei to hendelsane. Men då kan vi risikera å summera samme utfall fleire gonger. Hvis A og B overlappar vil vi i summen P(A) + P(B) leggja til dei utfalla som er felles to gonger. Det som er felles er jo snittet A ∩ B. Det betyr at for å finna sannsynligheten for unionen, så må vi trekkja frå P(A ∩ B).
Altså får vi regelen: P(A ∪ B) = P(A) + P(B) - P(A ∩ B) Dette kallast den generelle addisjonssetningen.

Hvis A og B derimot ikkje overlappar (dette kallast disjunkte mengder) så forenklar dette seg slik (sidan P(A ∩ B) = 0)
P(A ∪ B) = P(A) + P(B) Dette kallast addisjonssetningen for disjunkte hendelsar

Krysstabellar

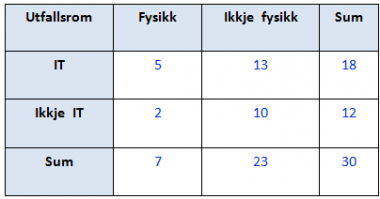
Ein annan måte å halda rede på kor mange element det er i ulike mengder etc. er ein såkalt krysstabell. Vi set opp ei ei kolonne for hendelsen A og ei for den motsatte. Tilsvarande lagar vi ei rad for B og ei for ikkje B. Tilslutt må vi også ha ei sum-rad og ein sum-kolonne. Tabellen under viser ein klasse på til saman 30 elevar. 18 av dei tar IT, og 7 av dei fysikk. Av disse er det 5 elevar som tar både fysikk og IT. Når vi veit dette kan vi rekna ut alle dei resterande tala. Antalet som ikkje tar IT er 30 - 18 = 12, og antalet som ikkje tar fysikk er 30 - 7 = 23. Så kan vi finna kor mange som tar IT, men ikkje fysikk (18 - 5 = 13), som tar fysikk men ikkje IT (7 - 5 = 2) og til slutt kor mange som hverken tar fysikk eller IT. (Enten som 12 - 2, eller som 23 - 13 = 10)

Når alle tala er på plass kan vi finna sannsynligheter: P(Fysikk eller IT) = (5 + 13 + 2) / 30 = 20/30 = 2/3. P(Fysikk og IT) = 5/30 = 1/6. Osv.

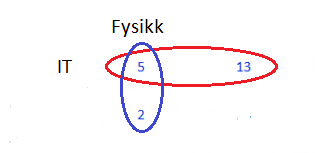
Denne situasjonan kunne vi også tegna med eit Venndiagram som på figuren under. Vi ser at disse fem som både tar fysikk og IT er altså snittet mellom dei to mengdene, mens unionen, består av 5 + 13 + 2 = 20 stk.
Krysstabell til Venn diagram

Multiplikasjonsprinsippet

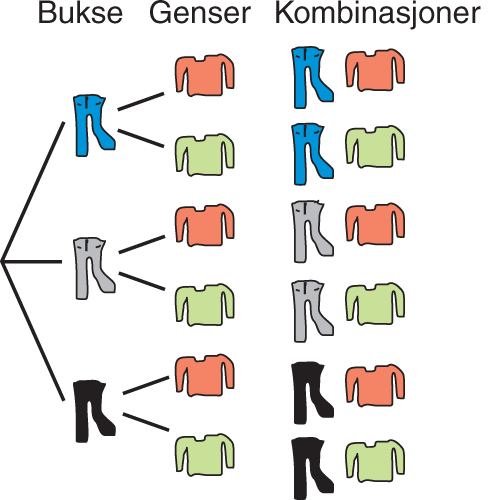
Hvis du har tre bukser og to gensarar så har du tilsaman 3 x 2 = 6 mulige kombinasjonar. Under er dette illustrert ved eit såkalt valgtre. Dette er eksempel på det såkalte multiplikasjonspronsippet. Hvis vi skal gjera fleire valg så finn vi antallet mulige kombinasjonar ved å multiplisera antall alternativ ved kvart valg.

Hvis vi har samme valg fleire gonger får vi ein grei formel. For eksempel to terningkast gir 6 * 6 = 6² = 36 muligheter. Fem mynt og kron etter kvarandre gir 2*2*2*2*2 = 2⁵ = 32 muligheter. Så hvis vi har n valg k gonger, blir formelen dermed at vi har n^k muligheter totalt.

Uavhengige og avhengige hendelsar

Eksempel 1: uavhengige hendelsar. Tenk deg at du skal ta ein liten test med bare to oppgaver, og sannsynligheten for å få rett svar er ein firedel for kvar av oppgavene. Då kan vi først tegna eit valgtre med følgande muligheter og tilhøyrande sannsynligheter.

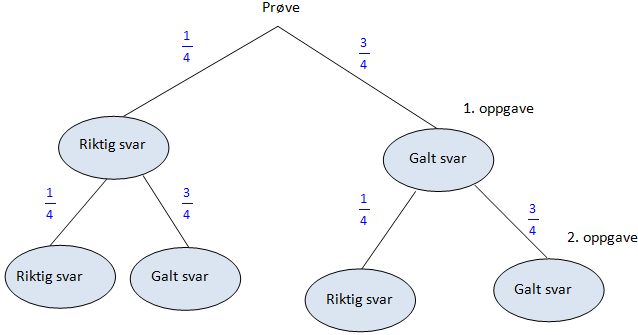
Merk at sannsynligheten for å få rett svar andre gong er den samme uansett om du har fåt rett første gong eller ikkje. Dette kallar vi for uavhengige hendelsar. Sannsynligheten for å få rett svar begge gongene blir då 1/4 * 1/4 = 1/16. Hvis vi definerer hendelsen A som "å få rett på første oppgave", og B = "å få rett på andre oppgave". så finn vi sannsynligheten for at både A og B skal inntreffa som produktet av sannsynlighetane for kvar hendelse: Vi kan skriva det som

P(A ∩ B = P(A) * P(B) Dette kallast for produktsetningen for uavhengige hendelsar

Eksempel 2: avhengige hendelsar. Hvis vi derimot for eksempel skal trekkja kuler frå ein kasse uten tilbakelegging så blir utrekningen litt forskjellig. Tenk deg at du har to blå kuler og tre raude i potten, altså [B,B,R,R,R], og du skal trekkja to gonger. Du hare då følgande muligheter:

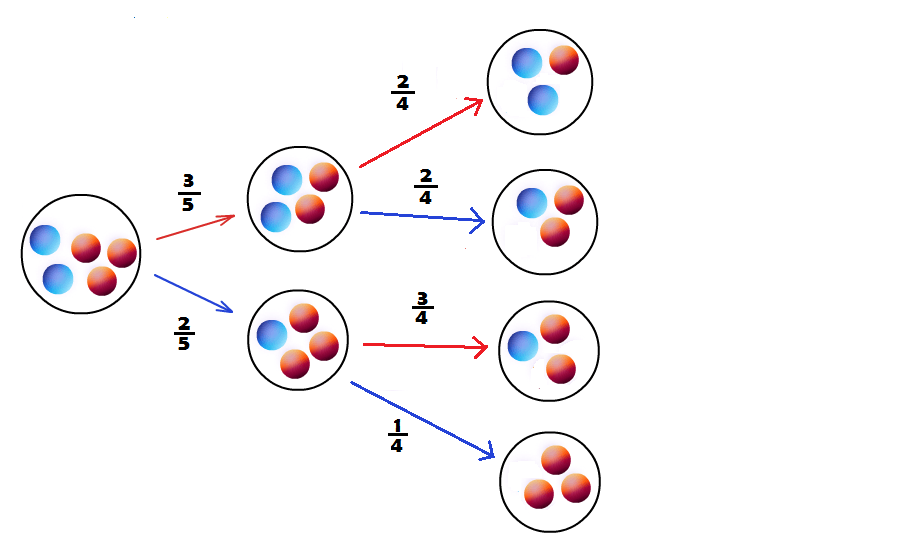
Sannsynlightene for å trekkja R første gong er lik 3/5, mens sannsynlightene for å trekkja R andre gong, hvis vi har trekt rødt første, er 2/4 sidan potten no er [B,B,R,R]. Sannsynligheten for å trekkja raud begge gongene blir derfor 3/5 * 2/4 = 3/10 (forkorta). Igjen har vi altså multiplisert dei to sannsynlighetene langs stien, men vi må skriva det på ein annan måte. Grunnen er at sannsynligheten for å trekkja rødt andre gong er avhengig av kva vi trekte først. Dette kallar vi for ein betinga sannsynlighet. Sannsynligheten for at vi trekk rødt andre gong (hendelse B) dersom vi alt har trekt rødt i første (hendelse A) skriv vi som P(B|A). Vi seier "sannsynligheten for B gitt A".

Vi kan skriva det som: P(A ∩ B = P(A) * P(B|A) Dette er den generelle produktsetningen.

Når det er slik, seier vi at hendelsane A og B er avhengige hendelsar.

Total sannsynlighet.

No kan vi spørja: Ka er sannsynligheten for å trekkja rødt andre gong, uavhengig av ka vi trekte første gong? Det vi spør etter er P(B). Vi ser at vi kan få til dette på to måtar. Enten ved først å trekkja rødt og deretter rødt, eller ved først å trekkja ikkje-rødt (dvs. blått), og så rødt. Sannsynligheten for å trekkja rødt andre gong er derfor summen av sannsynlighetane for disse to måtane. Den første har vi alt funne over. Den andre kan vi kalla P(A ∩ B = P(A) * P(B|A)

Alt i alt får vi altså: P(B) = P(A) * P(B|A) + P(A) * P(B|A)

Dette er det vi kallar for total sannsynlighet.

LENKER

Addisjon av sannsynligheter på NDLA.