Riemannsk (ikkje-euklidsk) geometri

Heilt sidan før Euklids Elementa kom har vi vore vane med visse setningar som er så innlysande at vi knapt tenkjer over om dei er rette. Eksempel er:

• omkretsen av ein sirkel er talet pi gonger diameteren
• vinkelsummen i ein trekant er 180 grader
• gitt ei linje L₁ og eit punkt p i planet, så fins det ei og bare ei linje L₂ som går gjennom punktet uten å kryssa den første linja (fig 1). Disse to linjene er parallelle.

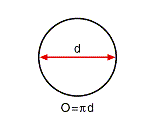
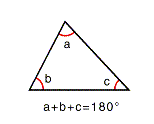
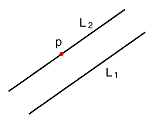
Fig 1. Euklidisk geometri i planet.

Men til tross for store anstrengelsar klarte ingen å bevisa disse setningane. Det viste til seg og med at dei ikkje nødvendigvis er sanne, bare under visse forutsetningar. Den euklidiske geometrien fungerer nemlig bare så lenge ein reknar med plane flater. La oss sjå kva som skjer når vi prøver disse tre reglane på ei kuleflate:

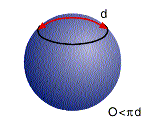
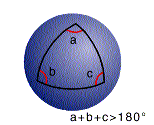
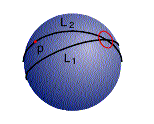
Fig 2. Riemannsk geometri på ei kuleflate.

Som figur 2 viser er omkretsen av sirkelen mindre enn pi gonger diameteren, vinkelsummen i ein trekant er større enn 180 grader og to dei to linjene L₁ og L₂ som er parallelle i p kryssar kvarandre! Det fins altå ikkje parallelle linjer på ei kuleflate.

Geometrien på ei kuleflate kallast elliptisk geometri eller Riemannsk geometri etter den tyske matematikaren, Georg Bernhard Riemann som først studerte denne.

Innvendingar

• Det sanne midtpunktet i sirkelen befinn seg ikkje på kuleflata, men litt under, og dersom vi bruker avstanden fra sirkelen til dette punktet som den sanne radien, så har vi fremdeles at O = π · d
• Sidene i trekanten abc er ikkje rette, og det same kan vi sei om "linjene" L₁ og L₂ som egentlig er storsirklar på kuleflata.

Delvis svar

Merk at både plan og kuleflater todimensjonale rom. Forskjellen er at planet er flatt, mens kuleflata er krumma. Men vi må forlanga at alle punkt og linjer som vi snakkar om befinn seg i dette todimensjonale rommet. 

• Derfor kan vi ikkje definera eit punkt utanfor flata som sentrum av sirkelen. Sentrum må definerast som det punktet på flata som har samme avstand til sirkelen, og denne avstanden definerer vi som radien.
• Av samme grunn kan vi ikkje laga linjer som er "rettare" enn kurven ab, fordi då går vi også frå 2D til 3D. Kurven ab på kuleflata er den kortaste og dermed rettaste veien frå a til b. Vi kan derfor definera dei som rette linjer, og derfor kallar vi også L₁ og L₂ for rette.

Det var ikkje før i 1868 at Beltrami beviste at ikkje-Euklidsk geometri er like logisk konsistenst som den valige Euklidske. Men den har likevel fått stor anvendelse i den generelle relativitetsteorien.