Bevis for Pytagorasetningen
Pytagoras sin setning seier at for ein rettvinkla trekant, så er summen
av kvadrata av katetane lik kvadratet av hypotenusen. Hvis vi ser på
trekanten under, men katetane a og b, og hypotenusen lik c, så kan vi
skriva den som: c² = a² + b². Dette kan illustrerast ved å laga
eit kvadrat til kvar side, som vist under:
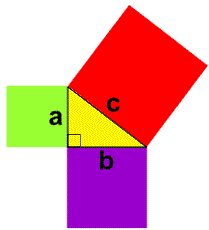
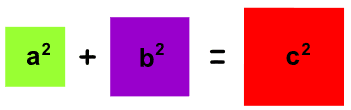
Eit typisk eksempel får vi når katetane a = 3 og b = 4. Då får vi at c = 5, fordi 3² + 4² = 5².
Det fins over hundre bevis for setningen, så her skal vi bare sjå på noken av dei vanligaste.
Bevis 1
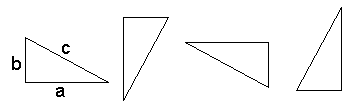
Vi startar med å laga tre kopier av trekanten vår, som vi så roterer med
90°, 180°, og 270°, henholdsvis. Kvar av disse fire trekantane har arealet
ab/2. No kan vi setja dei saman slik at vi får ein firkant med side c:
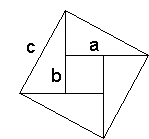
Men denne firkanten har eit kvadratisk felt i midten med side lik (a - b).
Hvis vi adderer arealet til dette kvadratet, dvs. (a - b)² og dei fire
trekantane, dvs. 4·ab/2 = 2ab, så må vi få c²:
c² = (a - b)² + 2ab
= a² - 2ab + b² + 2ab
= a² + b²
Bevis 2 (aka det kinesiske beviset)
Vi startar med dei same fire trekantane som i stad, men denne gongen set vi dei saman slik at dei lagar eit stort kvadrat med sider (a+b) og nok ein gong eit kvadratisk felt i midten. Men her er sida c. Vi kan no rekna ut arealet av det store kvadratet på to forskjellige måtar, og disse to må gi same resultat.
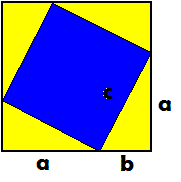
Altså har vi: (a + b)² = 4·ab/2 + c²
Ved å forenkla denne får vi Pytagoras.
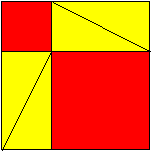
Geometrisk variant:
Ved å stokka om på bitane, ser vi umiddelbart at dette stemmer: Det raude arealet må vera likt det blå i figuren over.
Bevis 3 Formlike trekantar.
Vi startar med den opprinnelige trekanten med kateter a og b, og hypotenus c. Høyden (den stipla linja) deler c inn i to deler x og c-x.
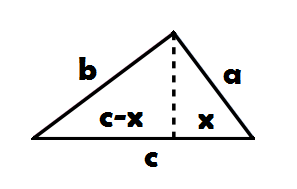
Den lille trekanten til høgre er likeforma med den store. Det gir oss
likning I: a/c = x/a, dvs. a² = xc
Den mellomstore trekanten til venstre er også likeforma med den store. Då
får vi likning II: b/(c-x) = c/b eller b² = c(c-x)
Summerer vi venstresidene og høgresidene av ligning I og II, blir dette:
a² + b² = xc + c(c-x), dvs.
a² + b² = c²
I ein litt annan variant kan vi løysa likning I og II for å finna uttrykk for dei to bitane av c som har lengdene x og c-x:
Likning I gir: x = a² / c, og likning II gir: c-x = b²
/ c. No kan vi finna areala av dei to rektangela ved å multiplisera
med høyden c.
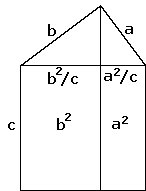
Vi ser at areala då bli hhv, b² og a², som til saman må bli c². Eit berømt bevis etter Euklid bruker same tankegangen, men er litt meir omfattande, så det tar eg ikkje med her.
Geometrisk variant:
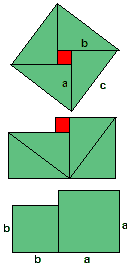
Ein tredje variant er å starta med figuren til venstre under, og transformera den i to steg. Først drar vi toppsidene av den rosa og den blå firkantane opp mot midten. På denne måten får vi to parallellogram som har samme høyde som dei opprinnelige kvadrata (nemlig b og a). Dermed er areala av parallellogramma lik areala av kvadrata vi starta med. Så dytter vi ned frå toppen, med andre ord skyv vi sideflatene i dei to parallellogramma nedover. Då vil også areala forbli uendra. I sum har vi omforma dei to kvadrata vi starta med til å bli to rektangel. Som vi ser er summen av areala av disse to rektagela lik arealet av det store kvadratet under. Dermed har vi vist Pytagoras sin setning.
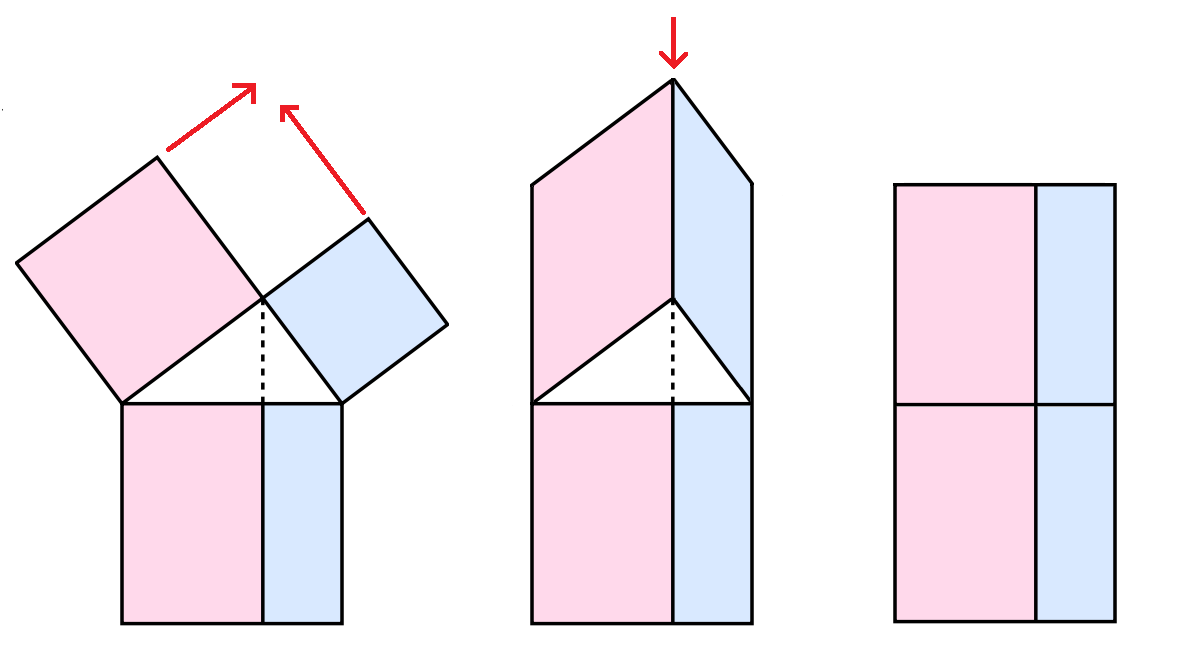
Under kan du sjå ein animasjon som viser dette:
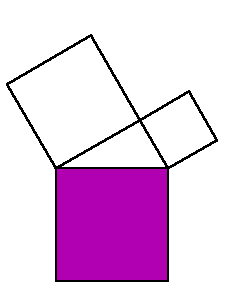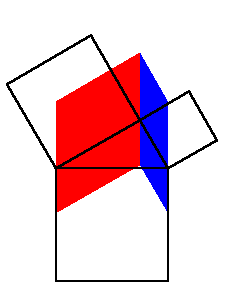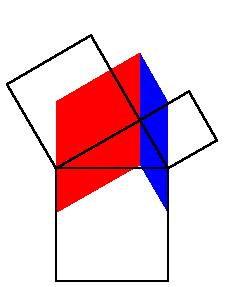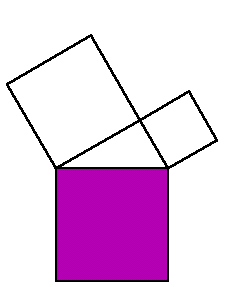 Ein variant av dette kan du sjå
her.
Ein variant av dette kan du sjå
her.
Bevis 4
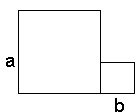
Vi startar med to kvadrater med sider a og b, henholdsvis. Vi plasserer
disse side ved side, som vist i figuren over. Det totale arealet av disse er
då a²+b².
Så tegner vi inn to like trekantar med sider a og b, og hypotenus lik c. Sjå
figuren til venstre under.
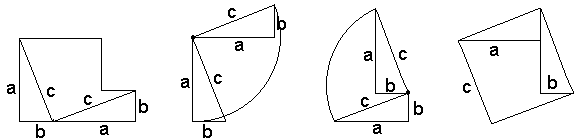
No kan vi skjera laus disse to trekantane, rotera dei 90°, den eine med klokka og den andre mot klokka. Deretter limer vi dei på igjen og får figuren til høgre. Den resulterande figuren er eit kvadrat med side c og areal c².
Bevis 5
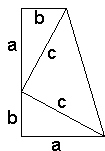
Dette beviset er tilskrive den amerikanske presidenten J. A. Garfield i 1876. Figuren viser eit trapes sett saman av to trekantar med katetar a og b, og hypotenus c, samt ein trekant med kateter c. Hvis vi bruker formelen for arealet av eit trapes blir det: A = (a + b)/2·(a + b). Husk at høyden i trapeset er a + b. Hvis vi reknar ut det same arealet ved å leggja saman areala av dei tre trekantane, så får vi: A = ab/2 + ab/2 + c·c/2. Når vi set disse to uttrykkja for A lik kvarandre og forenklar, så får vi nok ein gong: a² + b² = c².
Bevis 6
Trekantane vi brukte i Bevis 1 over, kan puslast saman på ein annan måte, som viser Pytagoras setning ganske greit:
LENKER
Vannversjonen (frå QI)
