Optikk og fotografi

Dei første optiske instrumentet var kanskje auget, men dei første menneskelagde instrumenta vart til for å hjelpa synet. Kanskje var enkle linser i form av steinar av kvarts i bruk som forsstørrelseglas eller brennglas alt i det gamle Egypt og Mesopotamia. I alle fall var brennglas kjent av grekarane og romerane. Dei første brillene skal ha blitt laga i nord-Italia, sannsynligvis i Pisa, rundt 1290, og i 1609 starta Galileo den moderne astronomien ved å retta eit teleskop mot Jupiter. Seinare har vi fått mikroskopet for å studera veldig små objekt. Så optiske instrument har i høg grad blitt brukt til å utvikla vitenskap. Samtidig er opptikk ein vitenskap i seg sjøl. Som ein liten introduksjon til dette feltet skal vi kikka litt på optikken i linser og kameraobjektiv. Det skadar ikkje å kunna litt om fysikken bak dette, spesielt Snells brytningslov.

Linser og objektiv

I fotografi skiller vi mellom ei linse og eit objektiv. Ei linse er eit stykke glas, eller gjennomsiktig materiale som, på grunn av Snells brytningslov, bøyer lyset. Det fins to hovedtypar: konveks (samlelinse) og konkav (spredelinse). Disse kan igjen delast inn i undertyper: I figuren under ser vi frå venstre: konkavkonveks (også kalla meniskforma konveks), plankonveks, bikonveks, konvekskonkav (også kalla meniskforma konkav), plankonkav og bikonkav.

Eit objektiv er då vanligvis samansett av ganske mange linser som samvirkar. Hvis du les engelsk litteratur bør du merka deg at der kallast objektivet merkelig nok for lens, mens dei enkelte linsene blir kalla lens elements. Ikkje sjelden har eit objektiv over ti linser. Men det er ikkje nødvendigvis betre jo fleire linser det har. Eit vidvinkelobjektiv kan feks. sjå slik ut:

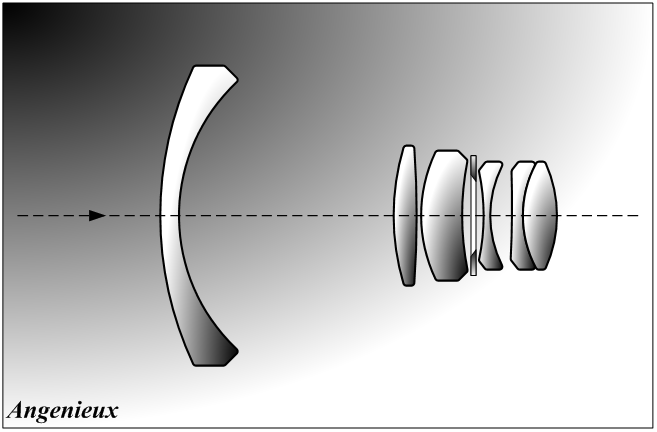
Bildet viser eit såkalt retrofokus-objektiv med seks linser, konstruert av Pierre Angénieux i 1950.

Brennvidde, forstørring og bildevinkel (field /angle of view)

Hvis du bruker et forstørrelsesglas eller ei liknande konveks linse, så kan du samla lyset frå sola i meir eller mindre eit punkt. På denne måten kan du tenna fyr på eit papir. I praksis vil ikkje strålene traffa nøyaktig på same plass (meir om dette nedanfor) men vi skal inntil vidare anta at dei gjer det, dvs at vi har ei perfekt linse. 

Ord og uttrykk.

Sidan sola er så langt unna kan vi med god tilnærming betrakta dei innkommande solstrålene som parallelle. Punktet som lyset då samlar seg i kallast brennpunktet, og avstanden (omtrent) frå midten av linsa til brennpunktet, kallast brennvidda, eller fokallengda (focal length på engelsk). Som regel bruker ein bokstaven f, for brennvidda.

For objektiv som består av mange linser er dette litt komplisert. Brennvidda er då avstanden frå brennpunktet til linsa sitt optiske sentrum. Men dette er eit litt dårlig definert begrep, og det er faktisk slik at det optiske senteret i nokon tilfeller (for eit vidvinkelobjektiv) kan vera nærmare filmplanet enn den nærmaste linsa, og i andre tilfeller (for eit telobjektiv) kan det vera lenger borte enn den fjernaste linsa. På den måten kan teleobjektiv gjerast kortere enn brennvidda. Men ta det med ro, vi skal bare sjå på eksempel med enkeltlinser!

På same måten som strålene frå sola samlar seg i brennpunktet, så vil strålene frå eit fjernt objekt som vi vil ta bilde av, samla seg i brennpunktet. Det betyr at når vi fotograferer fjerne objekt, så vil filmplanet eller bildeplanet (altså der bildebrikka befinn seg, for å bruka eit moderne språk) gå gjennom brennpunktet. Men hvis derimot objektet ganske nær, vil strålene frå det aldeles ikkje vera parallelle. Det betyr at dei ikkje vil samlast i brennpunktet, men i eit punkt lenger bak, slik figuren under viser. Då vil bildeplanet altså ligga lenger bak. Her er objektet vi vil ta bilde av eit ganske lite tre (kanskje ein figur?)

Strålegang

For å finna ut kor punktet P i toppen av treet vil bli avbilda, ser vi på tre ulike lysstråler frå P som går gjennom linsa og samlar seg igjen i punktet P'. Den raude strålen, som er parallell med den stipla linja, vil brytast og gå gjennom brennpunktet B' på bildesida. Den grøne hovedstrålen går gjennom sentrum av linsa, og vil fortsetja ubøyd. (Egentlig vil den brytast to gonger, og komma ut som ein parallell stråle, men ørlite forskyvd. Men denne forskyvinga kan vi sjå bort frå, for ei tynn linse.) Den blå strålen, som går gjennom brennpunktet B på objektsida, vil brytast og komma ut som ein parallell stråle. Alle disse tre vil møtast i P'. For å få eit skarpt bilde er det altså her, gjennom punktet P', dvs. som bildeplanet må vera for at treet skal vera i fokus. Dette betyr at hvis avstanden frå objektet til linsa endrar seg, så må også avstanden frå linsa til bildeplanet endra seg. Dette oppnår vi ved å skyva linsene i objektivet fram og tilbake i forhold til bildebrikka. Det er dette vi kallar å fokusera.

Linseformelen og forstørring

Vi vil no rekna på kor langt får bildeplanet må vera i eit konkret eksempel. Men først treng vi to formlar. Vi tar utgangspunkt i ein variant av den same figuren (under), og begynner å definera ein del avstandar. Objektet vårt er no ei blå pil som har høyden h_o og er i avstanden d_o frå linsa. Den blå pila blir avbilda som ei gul pil som har høyden h_i, og er i avstanden d_i frå linsa. Avstanden frå linsa til brennpunktet B' kallar vi, som før, for f. No ser vi av figuren at trekanten PQR (den blå) er likeforma med RP'Q' (den raude). Dermed kan vi setja opp likning I: h_i/ h₀ = d_i / d_o. Vidare er trekanten RB'S likeforma med B'P'Q. Og det gir oss likning II:  h_i/ h₀ = (d_i - f) / f. No ser vi at venstresidene av likningane I og II er like. Det betyr at også høgresidene er like. Altså har vi at d_i / d_o = (d_i - f) / f. No skal vi bare ordna litt. Skriv vi om høgre sida ser den slik ut: d_i / d_o = d_i / f - 1. Og hvis vi deler på d_i i alle ledd, så får vi 1 / d_o = 1 / f - 1 / d_i. No er vi egentlig framme, men hvis vi flytter over leddet 1 / d_i , så får vi formelen slik den vanligvis blir skriven:  1 / d_i + 1 / d_o = 1 / f . Dette kallast linseformelen, og gjeld for tynne linser.

Forholdet mellom størrelsen på avbildningen og originalen kallar vi forstørringen, og får ofte bokstaven m (for magnification). Vi har at m = h_i/ h₀. Men likning I gjer at vi heller kan skriva: m = d_i / d_o. Då har vi dei to formlane vi var ute etter:

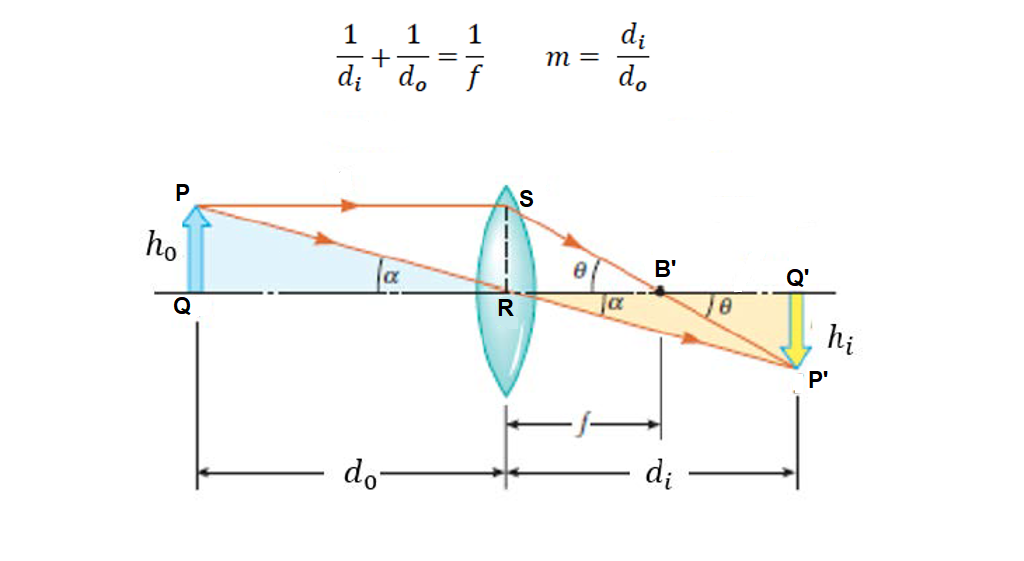
Eksempel: Eit normalobjektiv har gjerne er brennvidde på f = 50 mm (5 cm). La oss sei at vi vil fokusera på ein blom som er d_o = 30 cm unna. Kva avstand d_i treng vi då mellom linsa og bildebrikka? Vi set inn i linseformelen og får: 1/d_i + 1/30 = 1/5. (Her må vi huska å bruka same enhet alle stader.) Altså: 1/d_i = 1/5 - 1/30 = 1/6. Det betyr at d_i = 6 cm. Dette gir ein forstørring m = d_i / d_o  = 6 / 30 = 1/5 (eller 0,2). Det vil sei at blomen på bildebrikka (eller filmen) er ein femtedel av originalen. Kanskje er dette godt nok for deg. Men mange som driv med makrofotografering, vil gjerne ha større forstørring. I såfall treng vi å auka avstanden mellom linsa og bildebrikka. Men alle objektiv har ei grense for kor langt ut du kan skru det. For mange normalobjektiv ligg det rundt dei 6 cm som vi fant. Det betyr at dei klarer ikkje å fokusera veldig mykje nærmare enn 30 cm. Dette kallast nærgrensa. Det er mange løysingar på dette. Det enklaste er kanskje å setja inn såkalte mellomringar mellom objektivet og kameraet. Det aukar d_i, og dermed kan du komma nærmare. Ein liknande måte er å bruka ein belg, som du kan endra lengda på. Men du kan også kjøpa dedikerte makroobjektiv. Les meir om makrofotografering.

Bildevinkel (angle of view), brikkestørrelse og crop-faktor

Vi skal sjå at brennvidda bestemmer kor mykje av synsfeltet som eit gitt objektiv klarar å fanga på ei bestemt bildebrikke eller på ein film med bestemt størrelse. Dette kallast for bildevinkel, eller noken gonger visningsvinkel. Denne vinkelen kan målast i tre ulike retningar: diagonalt, horisontalt eller vertikalt. Sjå figuren under.

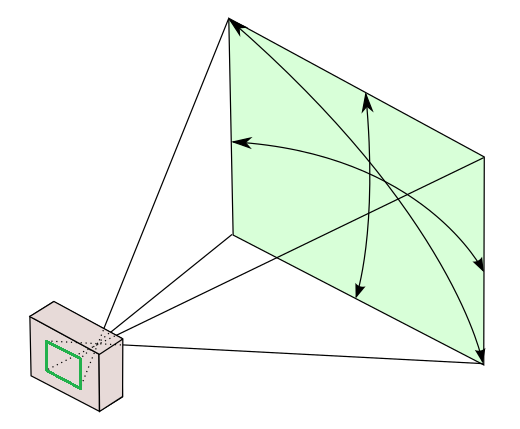
På neste figur dekkar "objektet" (markert med den grøne dobbeltpila) heile bildet. Bildevinkelen (α på figuren), er då vinkelen mellom dei to raude strålene som går frå ytterkantane av objektet til ytterkantane av bildet. I figuren er den halve bildevinkelen α/2 markert. Vidare er d dimensjonen på sensoren i den retningen ein vil måla bildevinkelen i, og f er den effektive brennvidda på objektivet. Figuren brukar stor bokstav F for dette, og kallar avstanden frå objektet til linsa for S₁ og avstanden frå linsa til bildebrikka for S₂.

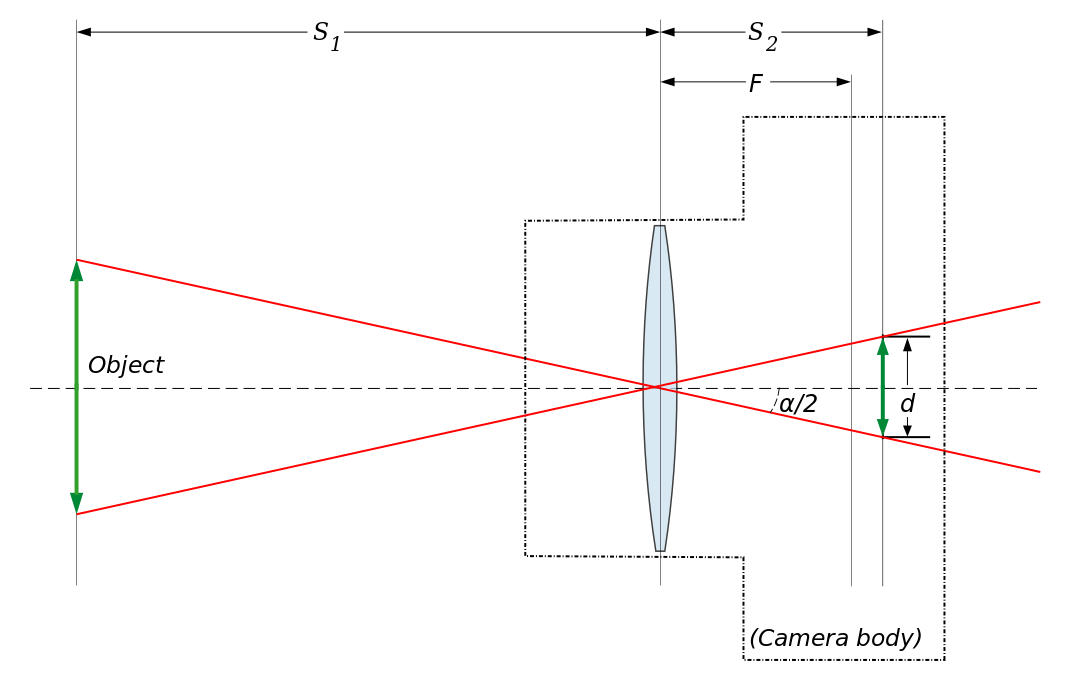
Vi ser at tangens til α/2 er gitt ved d/2 dividert med S₂. Hvis vi tenkjer oss at vi flyttar "objektet" ut til uendelig (tenk på det som kor stor del av horisonten vi får med på bildet), så blir S₂ lik f. Altså har vi at tan(α/2) = d/2f. Bildevinkelen α, er dermed gitt ved formelen (REF) :

α = 2 * tan^-1(d/2f))

Eksempel:

For å rekna på dette treng vi dimensjonane på bildebrikka. Figuren under viser dei relative størrelsane på tre vanlige typar sensorar eller bildebrikker.

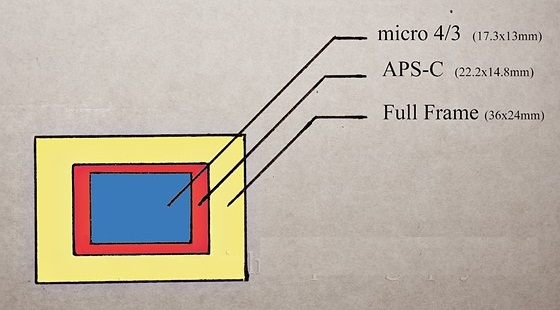
Som vi ser, er sensoren på eit såkalla fullformat-kamera 36mm x 24mm. Dette var det vanligaste formatet i gamle dagar med film, og noken kallar det fremdeles for "35mm"-format fordi filmrullen er 35 mm tver over. La oss sei at vi vil finna bildevinkelene diagonalt. Då kan vi rekna ut diagonalen i brikka med Pytagoras, og vi får d = 43.3 mm. La oss sei at vi har eit objektiv med brennvidde på f = 50 mm, dvs. det som kallast "normalobjektiv" for dette formatet. Då pluggar vi d og f inn i formelen, og får α = 43.3° .

No kan vi endra objektiv til f  = 100mm, dvs. ei kort telelinse. Når vi puttar inn f og d no, får vi α = 24.4°.

Altså: kort brennvidde gir stor bildevinkel, mens lang brennvidde gir liten bildevinkel.

Men la oss no sei at vi flyttar det 50mm-objektivet vi hadde først over på eit kamera med micro 4/3-sensor. I praksis er ikkje det så rett fram, for ulike kamera har forskjellige fatningar. Men når vi, som her, går frå ei  stor brikke til ei mindre, lar det seg ofte gjera med ein overgang.  Som figuren viser, har micro 4/3-sensoren dimensjonane 17.3mm x 13mm. Det gir ein diagonal d = 21.6 mm. No gir formelen oss at α = 24.4°. Altså den same bildevinkelen vi hadde med 100mm-linsa for fullformat.

Med andre ord: same brennvidde på eit kamera med mindre bildebrikke gir mindre bildevinkel. Så det som er eit normalobjektiv for eit fullformatkamera, blir ei telelinse for micro 4/3-kamera.

Vi seier at micro 4/3-sensoren har ei crop-faktor på 2. Det vil sei at vi må ganga brennvidda med to for å få same bildevinkel på eit micro 4/3-kamera (feks har Olympus og Panasonic slike kamera). Ei anna vanlig brikke er APS-C, som kjem i to variantar. Den som Fujifilm bruka på sine kamera med X-fatning har cropfaktor 1.5, mens Canon har ein del kamera med faktor 1.6. Så fins det også både større og mindre sensorar enn dette.

Her er ein kalkulator som reknar ut bildevinkelen når brennvidde og sensortypen er gitt.

Forskjellige bildevinklar passar til forskjellig bruk. For eit fullformatkamera er ein vanlig inndeling som følger, med vanlige bruksområder i parentes:

• 14 – 28mm: vidvinkel.  (landskap, arkitektur og interiør)
• 24 – 85mm: vidvinkel (gate og event fotografi)
• 50 – 85mm: normal til kort tele. (ofte brukt for portrett)
• 60 – 120mm: kort tele. (gjerne makro, men også her portrett)
• 300 – 600mm: telelinse (sport og dyreliv)

For andre format må du altså ganga med cropfaktoren. Men husk at bruksområda ikkje er hogd i stein. Det er du som fotograf som bestemtte ka slags objektiv du skal bruka i ein gitt situasjon.

Lysstyrke og blendar

Ein av dei viktige egenskapane til eit objektiv, er kor lyssterkt det er. Det betyr kor mykje lys det fangar. Jo større maksimal åpning eit objektiv har, jo større lysstyrke har det. Med lyssterke objektiv kan vi bruka hurtigare åpningstider for lukkaren. Vi treng ein viss mengde lys til lysbrikken eller filmen, og lysmengden er produktet av blenderåpning og lukkertid. Doblar vi blendaråpningen kan vi halvera lukkartida. Med håndholdte kamera er det ei grense for kor lang lukkartid vi kan bruka, før bildet blir uklart sjøl om denne grensa blir pusha av moderne kamera med stabilisering. Lyssterke objektiv, som også kallast hurtige objektiv, er derfor er veldig ettertrakta, men som regel også veldig dyre.

Eksempel på to objektiv med same brennvidde (85mm), men ulik lysstyrke: f/1.8 til venstre og f/1.2 til høgre. (Av Autopilot - Own work, CC BY-SA 3.0, Link)

Lysstyrken er oppgitt ved det såkalte blendartalet ≡ f/D, der f er brennvidda og D er effektiv diameter på lysbunten som slepp gjennom blendar og objektiv. Blendartalet er ofte oppgitt som feks. f/2. Det betyr at diameteren for åpningen er halvparten av brennvidda, mens f/4 betyr at det bare er ein fjerdedel. Så mindre blendartal betyr større lysstyrke.

Inne i objektivet sit det ein blendar som gjer at vi kan gjera åpningen mindre. I tillegg til å regulera lysmengden, har blendaråpningen betydning for dybdeskarpheten og kor uklart dei ufokuserte delene av bildet blir. Meir om det nedanfor. Det fins ulike typar blendarar, men den vanligaste er vel ein den såkalte irisblendaren, som består av eit antall tynne metall­blad (lamellar) som danner ein større eller mindre lysåpning.

Ein blendar kan ofte endrast med faste verdiar. Hvis vi skulle hatt ein skala der kvart stopp dobla eller halverte diameteren, så kunne den vore f/1, f/2, f/4, f/8 osv. Men sidan lysmengda som kjem inn er proporsjonal med arealet av åpningen, så er det meir praktisk med ein skala der diameteren blir multiplisert eller dividert med kvadratrota av to. Sidan arealet av ein sirkel er gitt som πr², så vil arealet dobla seg når vi multipliserer r med roten av 2. Derfor har dei fleste objektiv i dag skalaer som går slik: f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f/22, f/32, f/45, f/64, osv. Når vi opnar opp eit stopp på ein slik skala betyr det altså dobbelt så mykje lys inn, så lenge lukkartidene ikkje endrar seg. Hvis vi vil behalda same lysmengde, så må vi endra lukkertidane tilsvarande. Med andre ord: blendar f/5,6 og lukkartid 1/125s gir same lysmengde som blendar f/4 og lukkartid 1/250s, osv. 

Bokeh, uskarphetssirkelen og dybdeskarphet

Det er ofte både hensiktsmessig og uunngåelig at deler av bildet ikkje er i fokus. For eksempel er det ein vanlig teknikk i portrettfotografering å halda bakgrunnen ute av fokus, for derved å la personen tre fram tydeligare. Mange er då ute etter ein spesiell type uklarhet. Kvaliteten på uklarheten kallast boheh (boke), og er ein parameter, som mange fotografar er opptatt av. Bokehen er bestemt av optikken i objektivet, men også av blendaren.

Eksempel på bokeh: Slik kan mange fargepunkt sjå ut når dei ikkje er i fokus. JWCreations under

Circles of confusion: uskarphetssirkel

Vi antar fremdeles at vi har ei perfekt linse. Det vil sei at når vi har fokusert på ein bestemt avstand, så vil eit punkt som befinn seg i denne avstanden, også bli avbilda i eit punkt på brikka. Dette er vist i den midterste figuren under. Men ka skjer då med eit punkt som er litt nærmare enn det vi har fokusert på? Det viser det øverste figuren. Her ser vi at strålene ikkje klarer å samla seg heilt, og resultatet er at punktet blir smurt utover til ein sirkel. Dette kallast på engelsk Circle of Confusion (CoC). På norsk kan det gjerne kallast uskarphetssirkel. Det same skjer med punkt som ligg bakanfor fokus.

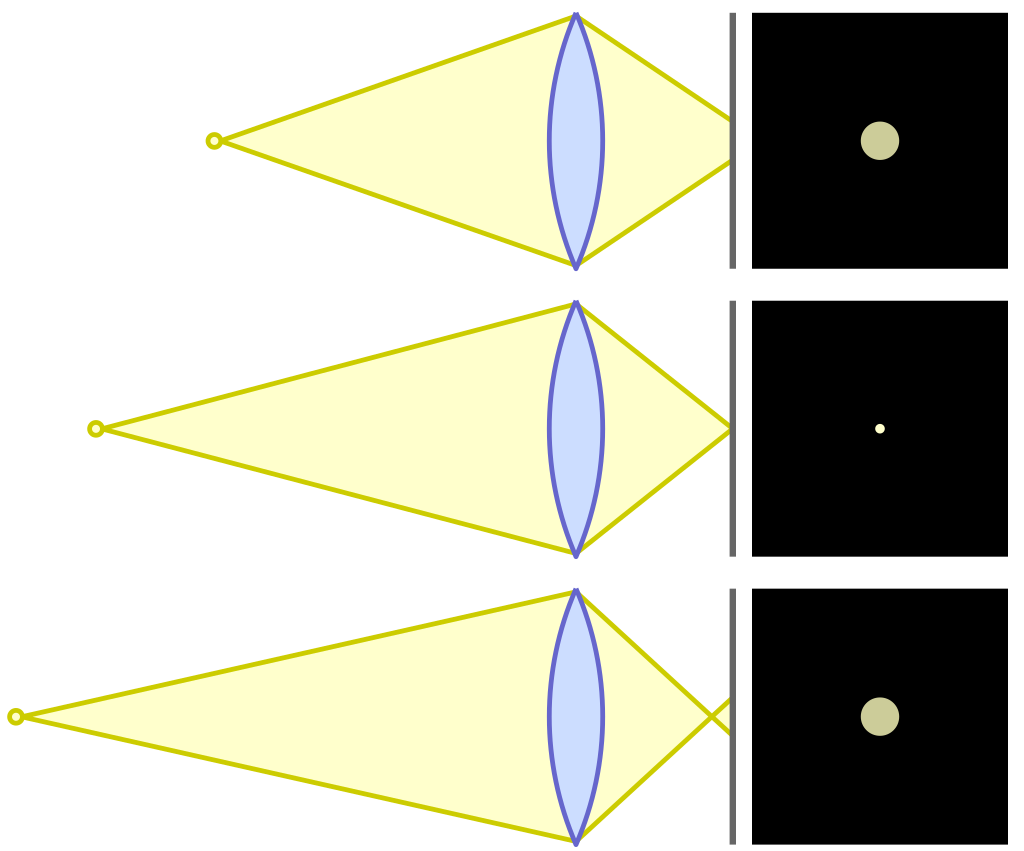
Original: Goliardico

Dybdeskarphet.

Men vi har ikkje behov for at alle punkt i motivet blir avbilda som perfekte, skarpe punkt. For vi har heller ikkje perfekte auger, og dermed er vi fornøyde når uskarphettssirklane er små nok. Det betyr at det vil vera eit område framfor og bak fokus, som vi opplever som skarpe. På figuren under er diameteren til den akseptable uskarphetssirkelen markert som Cd. Vi Ser at når punkt i avstanden d2 er i fokus, vil punktet bli avbilda som eit skarpt punkt (grøne linjer). Men også punkta som ligg i avstanden mellom d1 og d3 vil bli avbilda i punkt som er tilstrekkelig skarpe fordi linjene treff innanfor uskarphetssirkelen. Merk at fargen på strålene er her bare for å visa kor lyset frå d3, d2 og d1 treff. Altså: alle punkt i avstanden mellom d1 og d2 vil vi oppleva som skarpe i bildet.

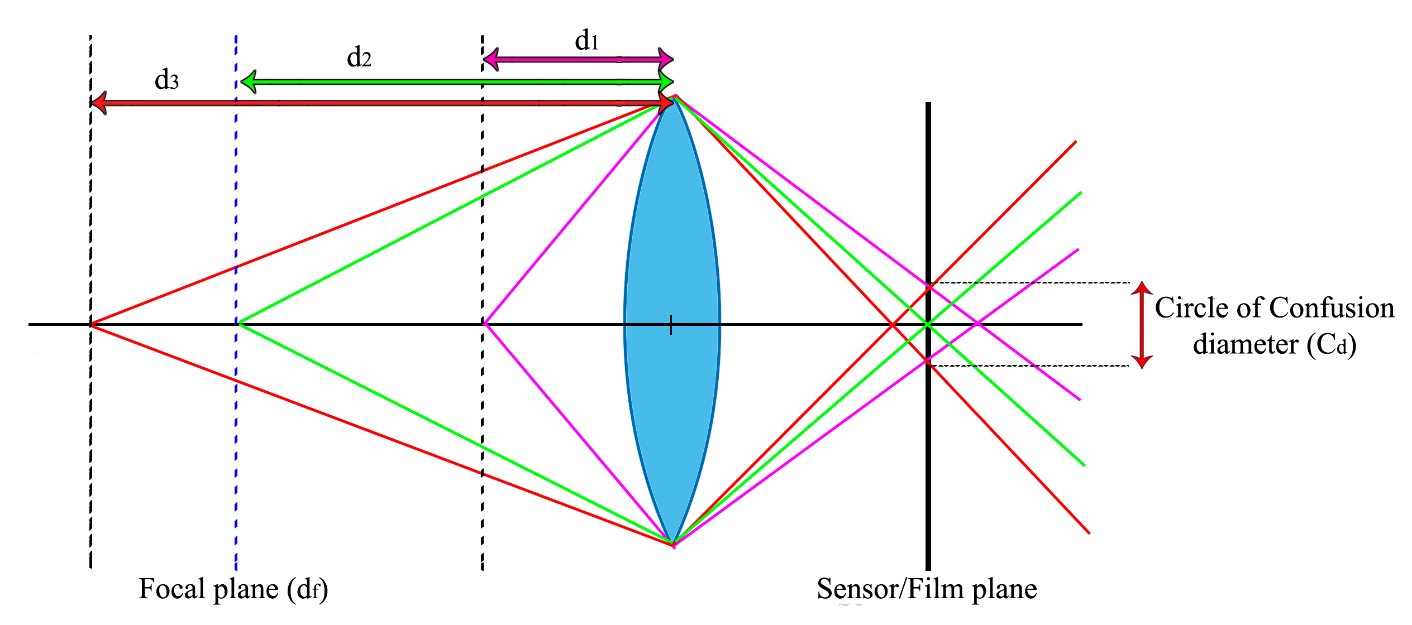
Når vi har eit stort området som er skarpt nok, så seier vi at vi har stor dybdeskarphet. Noken gonger, feks. når vi tar portrettfoto vil vi ha liten dybdeskarphet, men når vi tar landskapsfoto vil vi gjerne ha stor dybdeskarphet. Det kan vi oppnå hvis vi blendar ned. I den øverste figuren nedanfor vil eit objekt i objektplanet ha ein stor uskarphetssirkel, og vil derfor sjå uskarpt ut. Men i figuren under har vi blenda ned. Då blir uskarphetssirkelen mindre, og objektet vil sjå skarpt ut.

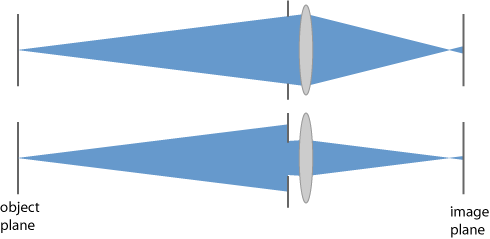
Altså: når vi vil ha stor dybdeskarphet brukar vi liten blendaråpning, og når vi vil ha liten dybdeskarphet, brukar vi stor blendaråpning.

Det er også andre faktorar som påvirkar dybdeskarpheten som avstand og brennvidde. Jo større avstand, jo større dybdeskarphet og omvendt. Og jo større brennvidde, jo mindre dybdeskarphet. Den siste samanhengen har den sideeffekten, at hvis du bruker kamera med mindre sensor, så treng du også bruka mindre brennvidde for å få same bildevinkel (som vi lærte ovanfor). Det betyr at du får større dybdeskarphet enn med tilsvarande fullframe-objektiv. Så det er altså lettare å få den uskarpe bokeh-effekten på fullframe-objektiv enn på andre.

Aberrasjon.

I fotografering bruker vi altså linser til å laga ein avbildning frå eit fysisk objekt til ein film eller ei bildebrikke. Ideelt sett vil vi då 1) at kvart punkt på objektet skal avbildast i eit eintydig punkt i bildet, og 2) at formene og linjene i objektet blir gjengitt korrekt i bildet. Men av mange grunnar skjer det avbildningsfeil, og dette kallast aberrasjon. Vi skal her bare sjå på den første typen, dvs det som fører til at punkt ikkje blir avbilda korrekt. Den andre typen aberrasjon kallast fortegning, og det får vi ta ein annan gong.

Sfærisk aberrasjon

Vi sa ovenfor at sollyset vil samla seg i brennpunktet. Men det gjeld bare for ei ideell linse. Inntil nylig har dei fleste linser blitt slipt slik at grenseflatene har form som ei (del av) ei kuleflate, dvs såkalte sfæriske linser. Men når vi reknar på slike linser med Snells brytninglov, finn vi at dei bryt lyset sterkare i randsona enn i sentralsona, slik at linsa ikkje har eit klart definert brennpunkt. Sjå figuren under. Sjøl om alle strålene opprinnelig kjem frå eit punkt langt til venstre slik at dei innfallande strålene er parallelle, så ser vi at strålene ikkje samlast i same punktet. Strålene frå randsona samlast i eit punkt, mens strålene frå sentralsona samlast i eit anna. Dette kallast sfærisk aberrasjon, og er tydeligare jo sterkare linsa er.

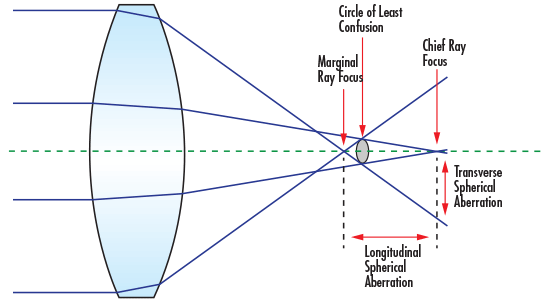
Ein enkel måte å redusera sfærisk aberrasjon på er å blenda ned, dvs. å gjera blendaråpningen mindre. Men betre å laga betre objektiv: det kan gjerast ved å bruka kombinasjonar av konvekse og konkave linser, eller ved å bruka asfæriske linser.

Kromatisk aberrasjon

Som om ikkje dette var nok, så vil lys av forskjellig farge bli brote ulikt når det går gjennom ei linse. Det er denne effekten som gjer at vi får regnboger og ser alle fargane når vi sender kvitt lys gjennom eit prisme.

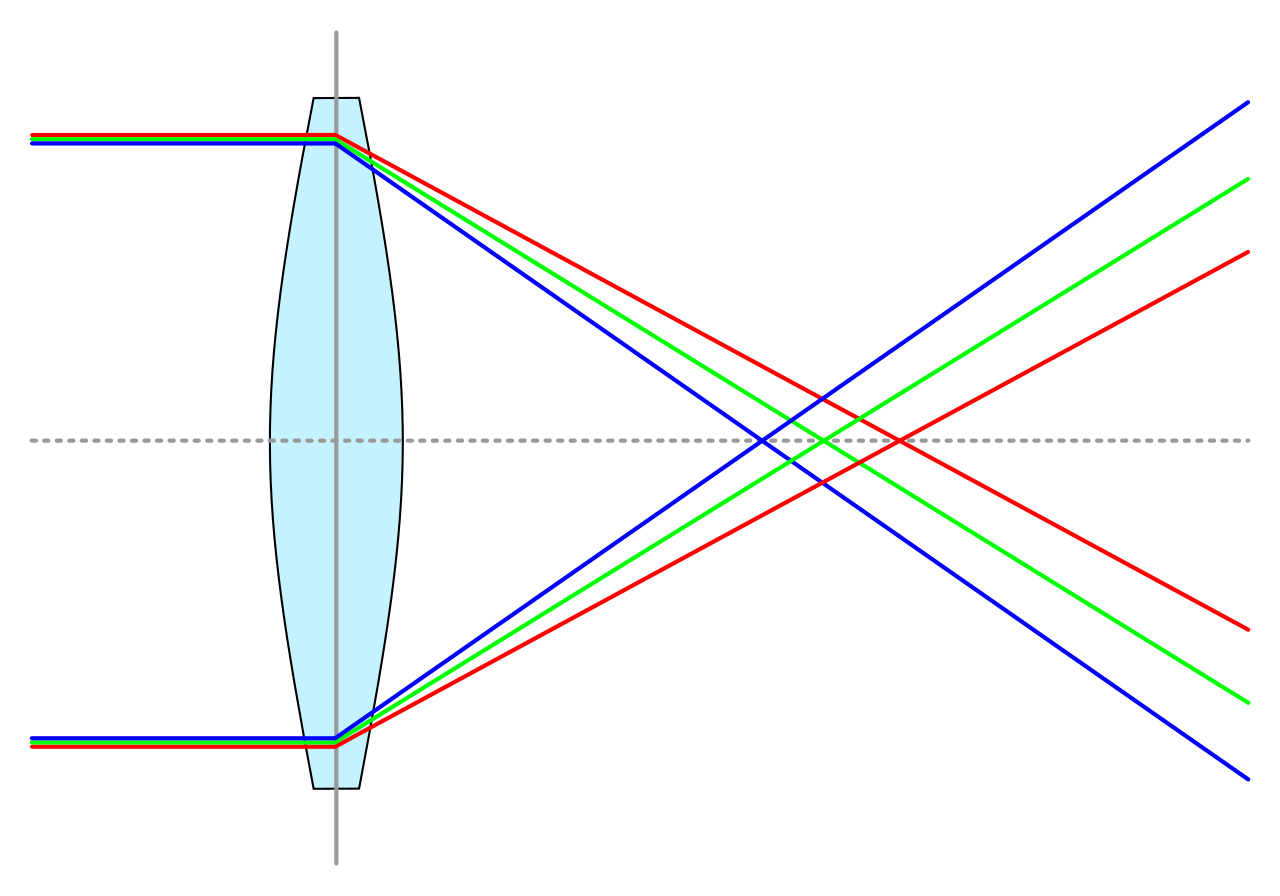
Også her vil det hjelpa å blenda ned objektivet. Men det er også stor forskjell på gode og dårlige objektiv.

Bøyning (diffraksjon) av lys

Frå det vi har sagt så langt ser det ut til at det å blenda ned er løysinga på alle våre probem. Men så enkelt er sjølsagt det ikkje. Problemet er at vi har lata som om lyset er stråler som alltid går rett fram gjennom ein åpning. Men det er ikkje tilfellet. Lys oppfører seg oftast som bølger, og bølger som går gjennom små opningar vil bli bøyd. Og jo mindre opningen er, jo sterkare blir effekten.

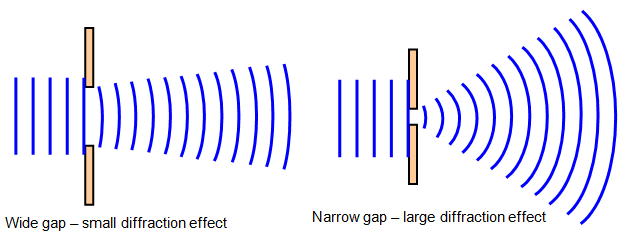
Det dette koker ned til er at det er grenser for kor mykje vi bør blenda ned, hvis målet er optimal skarphet. For etter kvart som blendaren blir mindre vil effekten av bøyning bli så stor at skarpheten begynner å bli dårligare igjen. Akkurat kor den optimale blendaren er, er det ingen fasit på, for her begynner dette å bli ganske messy. Likevel er det slik at korrekt blendar har like stor betydning for skarpheten som kvaliteten på objektivet.

Vidare

No har vi sett på noken viktige egenskaper ved linser og objektiv, og kva rolle disse spelar i fotografering. Men det er mange andre forhold som spelar inn for å laga eit godt objektiv. For eksempel spelar antirefleks-coating ein viktig rolle for å laga gode objektiv. Det betyr at fabrikkantane legg eit optisk belegg på linsene for å redusera refleks, og derved få betre lysstyrke. Vi har heller ikkje snakka om ulike typar filter, som blir brukt for å endra karakteren til det lyset som slepp gjennom linsa. For eksempel kan vi bruka fargefilter for å endra fargen, vi kan bruka gråfilter som reduserer lysmengda, eller vi kan bruka polarisasjonsfilter som bare slepp gjennom lys som er polarisert i bestemte retningar.

Sfærisk og kromatisk aberrasjon, som vi har sett på, påvirkar avbildninga av punkt over alt i bildet. Men to andre typar aberrasjon påvirkar bare punkt som ikkje ligg på den såkalte på den optiske aksen, dvs som ikkje ligg i sentrum av bildet. Dei kallast koma og astigmatisme. Andre problem som kan gjera seg gjeldande er refleksflekker (flare / ghosts) Sjå Understanding Lens Flare. og How to Eliminate Ghosting and Flare in Landscape Photography.

Vi har nevnt at alle objektiv har ein større eller mindre grad av fortegning. Det kan bety at linjer som er rette i verkeligheten, kan bli avbilda som bøyde, og det kan bety at linjer som er parallelle kan bli avbilda som konvergerande linjer, og graden av fortegning har med dei optiske egenskapene i objektivet å gjera. Men det er verd å merkja seg at noken gonger kan bildet bli uklart eller forvrengt av årsaker som har lite med optikken å gjera. For eksempel kan det vera pga. den såkalte rolling shutter-effekten eller det kan ha å gjera med begrensingar i bildebrikka etc. Slike ting har vi heller ikkje behandla her.

Til sist kan vi nevna at sjøl om kvalitetsoptikk har mindre slike problem så blir vi aldri heilt kvitt dei. Men med digitale bilder kan vi også kompensera for både aberrasjon, forvrenging og ein del andre problem vha. programvare. Slik programvare kan også endra på farge, skarphet og mykje anna.

LENKER

linse - optikk.

aberrasjon - optikk.

Openstax.org har ei bra kurs om optikk og moderne fysikk -> 2.4 Thin Lenses.

A Brief History of the Photographic Lens.

Astronomical Optics Part 4: Optical Aberrations.