Svingninger, lydbølger og musikk
1 Februar 2015Vi skal se litt på hvilke frekvenser som kan dannes i ulike stående bølger, på sammenhengen mellom frekvens og tonehøyde, og på klangfarge og hvordan denne kan påvirkes og endres.
Grunntonen.
På en gitar, fiolin eller et piano så er det svingende strenger som
produserer lyden, enten ved at vi klimprer, stryker eller slår på dem.
Strengene vil da få stående bølger. Siden strengen er fast i begge ender må
bølgen ha et knutepunkt der. Men vi kan også ha et eller flere knutepunkter
imellom. Den lengste
bølgelengden vi kan ha er når det ikke er noen mellomliggende knutepunkter, og
da vil bølgelengden tilsvarer det doble av strengens lengde
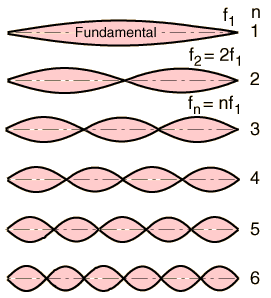 . Den tonen vi hører da kalles for grunntonen
, og er den lavest
mulige. Det er denne
man som regel hører best, og som bestemmer tonens frekvens. Hvis man vil endre
denne tonen, må kan man altså endre strengens lengde. Det er det som skjer
når musikeren trykker strengene ned på instrumentets hals med sine venstre
fingrer på en gitar eller en fiolin. Men man kan også endre tonen ved å endre
strengens stramming som man gjør når man stemmer instrumentet eller men kan
endre strengens masse. I praksis må man da skifte
streng.
. Den tonen vi hører da kalles for grunntonen
, og er den lavest
mulige. Det er denne
man som regel hører best, og som bestemmer tonens frekvens. Hvis man vil endre
denne tonen, må kan man altså endre strengens lengde. Det er det som skjer
når musikeren trykker strengene ned på instrumentets hals med sine venstre
fingrer på en gitar eller en fiolin. Men man kan også endre tonen ved å endre
strengens stramming som man gjør når man stemmer instrumentet eller men kan
endre strengens masse. I praksis må man da skifte
streng.
Overtonene
De tonene som har et eller flere mellomliggende knutepunkter kalles overtoner. Grunntonen og overtonene kalles ofte de harmoniske. Grunntonen heter da den første harmoniske, første overtone heter andre harmoniske, andre overtone heter tredje harmoniske etc. Disse er merket av på figuren med n = 1, 2 osv.
Vi kan nå finne en formel for frekvensen til de harmoniske uttrykt ved grunntonens frekvens. Siden bølgefarten er lik for alle disse bølgene gir formelen v = fλ at når bølgelengden blir halvert, så blir frekvensen doblet osv. Vi har altså at f2 = 2f1, f3 = 3f1 og generelt at fn = nf1. Det betyr at den den andre harmoniske har dobbelt så stor frekvens som grunntonen, den tredje tre ganger så stor som grunntonen osv.
Frekvens og tonehøyde
Vi vet at tonehøyden er en funksjon av frekvensen: jo høyere frekvens, jo høyere (lysere) blir tonen. Men sammenhengen mellom frekvens og oppfattet tonehøyde er ikke lineær. Det betyr at jo høyere vi går opp i registret, jo lengre avstand er det mellom halvtonetrinnene, målt i Hz. For å gå opp et halvtonetrinn, kan vi ikke legge til en fast frekvens. Vi må i stedet multiplisere frekvensen med en faktor. Det viser seg at når man dobler frekvensen, så oppfattes dette som et sprang på en oktav. Hvis vi antar at grunntonen er en lav C, så vil notebildet for de ulike harmoniske se slik ut:
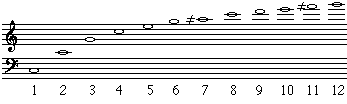
Legg merke til at mellom 1 og 2 er det en oktav, mellom 1 og 4 er det to oktaver, og mellom 1 og 8 er det tre oktaver. I musikkteorien kalles slike sprang mellom to noter for et intervall, og hvert intervall har sitt navn. Sammenligner vi notebildet med figuren over, kan vi finne hvilke frekvensforhold hvert intervall svarer til. Her ser vi eksempel på det:
| Forhold | Intervall | Eksempel |
| 2:1 | oktav (6 toner) | C - C |
| 3:2 | kvint (tre og en halv tone) | C - G |
| 4:3 | kvart (to og en halv tone) | G - C |
| 5:4 | stor ters (to heltoner) | C - E |
| 6:5 | liten ters (en og en halv tone) | E - G |
Det som er sagt over gjelder eksakt når man bruker en renstemt skala. I dag brukes som regel den tempererte skalaen. Her har man delt inn oktaven i 12 halvtoner som er jevnt fordel på en logaritmisk skala slik at man finner frekvensen til den neste tonen ved å multiplisere med samme konstant hver gang. Siden 12 steg skal tilsvare en fordobling, må altså denne konstanten være lik tolvteroten av 2 eller 1.05946. Men det fins mange andre skalaer, og i noen av disse deler man oktaven inn mer enn 12 deler. Dette kalles for mikrotonal musikk.
Klangfarge: tonekvalitet og
frekvensinnhold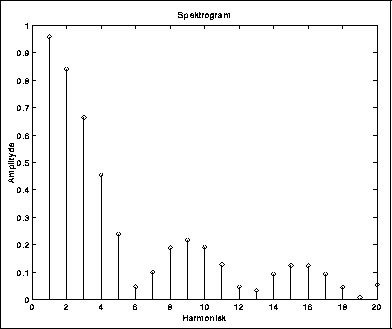
Når vi slå an en tone på en streng vil vi som regel få en svingning som er en kombinasjon av to eller flere av de harmoniske. Hvilke av de harmoniske som er tilstede og hvilket styrkeforhold de har til hverandre er det som avgjør tonens klangfarge. I noen tilfeller kan man "luke bort" bestemte overtoner. På en fiolin kan man feks. trykke forsiktig ned et sted på strengen og derved fjerne alle overtoner som har en buk på akkurat det stedet.
Ulike instrumenter har ulikt frekvensinnhold, og høres derfor forskjellige ut selv om de spiller samme note. Dette har sammenheng med hvordan tonen bli rprodusert. For eksempel vil en orgelpipe som er åpen i den ene enden og lukket i den andre ha en stående bølge som har knutepunkt i den ene enden og buk i den andre. Det betyr at for lengste bølgen bare får plass til 1/4 av bølgelengde Den neste får 3/4 og den tredje laveste får 5/4. Det betyr at vi kan sette 1/4λ1 = 3/4λ2 = 5/4λ3 = 7/4λ4 osv. Vi får da at f2 = 3f1, f3 = 5f1 og f4 = 7f1. Her ser vi at bare de odde harmoniske er tilstede, og dette kan høres for det påvirker orgelets klangfarge.
For å beskrive en klangfarge, er det ofte praktisk å beskrive lyden i et stolpediagram der deltonenes amplituder er vist som funksjon av frekvensen. En slik figur kalles et spektrogram, og kan avbildes ved hjelp av et måleinstrument som kalles en spektralanalysator eller spektrograf. Et spektrogram kan f.eks. se ut som i figuren over. Overtonene er gjerne svakere enn grunntonen. Legg også merke til de to "toppene" rundt den 9. og den 15. harmoniske. Slike topper er typiske i naturlig lyd, og kalles resonanser (fonetikerne bruker begrepet formanter).
Et interessant fenomen skjer når spekteret mangler grunntonen. Hvis hjernen synes at det "burde vært" en grunntone på en viss frekvens, vil vi kunne oppfatte en grunntone selv om det ikke finnes noen. Dersom vi f.eks. lager oss et spektrum med frekvensene 200 Hz, 300 Hz, 400 Hz etc., vil vi oppfatte en virtuell grunntone på 100 Hz, og det er denne noten vi hører.
Resonanskassen virkning på lyden
Men det er ikke bare hvilke bølger som blir produsert som har betydning. Like viktige er hvordan tonen blir modifisert. Fioliner, andre strykeinstrumenter og gitarer har en resonanskasse som skal forsterke lyden så den blir hørbar for publikum. Men ikke alle frekvenser blir like mye forsterket, og derfor vil kassen også endre lydens klangfarge. Både kassen og luften i kassen har sine egenfrekvenser og først hvis den produserte frekvensen stemmer med kassens får vi resonans i fysisk forstand. Dermed får vi distinkte topper som svarer til kassens resonansfrekvenser. Hvor disse toppene finnes og hvor høye de er, avhenger av kassens oppbygning. Derfor er klangen til en fiolin avhengig av en godt oppbygd kasse, og da forstår vi hvorfor fiolinbygging så vanskelig, og hvorfor gode fioliner er så ettertraktede.
Noe av samme skjer i sang, med en forskjellen at en sanger kan tilpasse sin "resonanskasse" for å få fram et best mulig resultat. Lyden blir produsert av stemmebåndene, men blir forsterket via hele systemet av hulrom som består av svelg og munnhule, nese og bihuler i kinn og panne. Sang er derfor en uhyre sammensatt disiplin som dels skal justere "motoren" dvs. lunger og omkringliggende muskler for å lage akkurat det trykket som trengs, dels justere stemmebåndene slik at den produserte lyden blir riktig, og dels justere resonanshulene for å modifisere tonen, og alt dette skal skje nøye avpasset. Og dette er bare den fysiske delen av sang...
