Masseenergi og massesvinn

Mysteriet med massen som forsvant

 

Vi ser at både ladningen og nukleontallet er bevart i denne reaksjonen: Ladningen på venstre side er 92 og det er det samme som ladningen på høgre side (90 + 2). Og det er 238 nukleoner på venstre side og det samme på høgre (234 + 4). Men kva så med massen? All fornuft tilseier at summeren av massene på høgre side av likningen må vera lik massen til urankjernen. For tross alt er det jo bare to nøytroner og to protoner som har "hoppa ut" av urankjernen. Dette kan vi testa ved hjelp av ein tabell. Massane tabellen er ofte oppgitt i ein enhet som heiter atommasseenheten. Den har symbolet u, og tilsvarer 1,66·10^-27 kg. Men vi treng ikkje å rekna om til kg for å samanlikna:

Venstre side: 238,05079 u
Høgre side: 234,04359 u + 4,002603 u = 238.046193 u
Med andre ord: massen er ikkje bevart i denne reaksjonen! Vi kan no finna kor mykje som har forsvunne: Differanse: 0.004597 u = 7.63102·10^-10kg.

Dette er en veldig liten masse, men den er ikke null, slik som vi skulle tru. Vi kallar dette for massesvinn, m_s. Kva er det som har skjedd her? Her kjem Einstein til unnsetning med sin formel

E₀ = mc²

Denne berømte formelen fortel at masse og energi er to sider av same sak. Masse er ein form for energi som vi kaller for masseenergi. Når det "manglar" en viss masse på høgre side, er det fordi en del av masseenergien har gått over i ein annen form! Energiloven seier jo at energi hverken kan skapast eller forsvinna, bare gå over til andre former. Og då har vi fleire muligheter. Den manglende masseenergien kan gå over til kinetisk energi (bevegelsesenergi), E_k og det forklarer korleis ein masse som ligg i ro plutselig kan senda ut ein alfapartikkel med stor hastighet. Men den kan også gå over til strålingsenergi, E_s i form av fotoner. Som regel vil vi få begge deler. Den ekstra energien kallast reaksjonsenergi, og det er den energien som blir utnytta i kjernereaktorar og i kjernevåpen.

Hvis vi ser på energiregnskapet i reaksjonen vår, så skal det gå opp. Men det går bare opp når vi ser på totalenergien, dvs. summen av masseenergi og reaksjonsenergi. Vi kan skriva det slik:

E = E₀ + E_k + E_s

E er bevart i ein kjernereaksjon. Det betyr at den totale energien før og etter reaksjonen er den samme. Hvis masseenergien i reaksjonen minker, så må reaksjonsenergien auke tilsvarende, og omvendt. Det betyr at vi kan skriva:

E_r = m_sc²

Et eksempel til: Rutherfords kjernereaksjon:

Venstre side 4,002603 u + 14,00307 u = 18.005673 u
Høgre side: 16,99913 u + 1,007825048 u = 18.00695505 u
Differanse: - 0.001282048 u.

Her er massen på høgresida større. Dette betyr at det må vera meir energi på venstresida enn bare masseenergien. Og det stemmer. For å få denne reaksjonen i gang må vi skyta inn alfapartikler med høg hastighet, slik at den får nok kinetisk energi til å vega opp for massedifferansen.

Fisjon og fusjon

Vi har sett at noken reaksjonar krever energi, mens andre reaksjonar frigjer energi. For at reaksjoner skal kunne frigjera energi så må vi få mindre masse etter reaksjonen enn før. For å sjå kva reaksjonar det er, kan vi lage ein graf som viser masse per nukleon som funksjon av nukleontalet A.

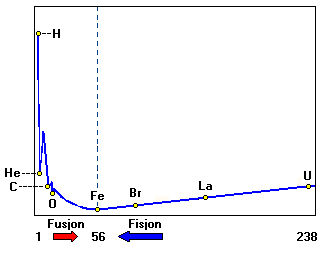
Den høgaste masse pr nukleon har hydrogen-kjernen. Så går det bratt ned til Helium, for deretter å synka litt svakare til vi kjem til jern (Fe) som er det lavaste punktet på kurva. Deretter stig grafen jevnt. For å få frigjort energi må vi bevega oss nedover på kurven. Grafen viser at det er to måtar å oppnå dette på:

1 Vi kan smelta saman lette kjerner. Dette kallast fusjon. Då startar vi på venstre side av grafen og beveger oss mot høgre. Eksempel på dette er deuterium-deuterium-fusjon:

 2 Vi kan spalta tunge kjerner. Dette kallast fisjon. Då starter vi på høgre side av grafen og beveger oss mot venstre. Eksempel på dette er uranfisjon: