Figurtal

Denne sida er tenkt som førstehjelp for matematikk 2P, og tilpassa Sinus-boka. Men den kan godt lesast av andre også!

Figurtal er eksempel på ei talfølge der kvart tal representerer antalet prikkar, linjer eller liknande i ein figur. Dette er lettast å forstå gjennom eksempel. Tenk deg at vi legg ut dei fire figurane med myntar som vist under:

Vi vil no finna ein regel eller ein formel som fortel oss kor mange myntar vi treng i figur nr n. Hvis vi kallar figurtal nummer n for F_n, så har vi at F₁ = 1, F₂ = 4, F₃ = 7 og F₄ = 10. Så legg vi merke til at frå figur to og utover kan vi laga neste figur ved å putta ein ny mynt inn i kvar av dei tre linjene som figuren dannar. For kvart figurtal kan vi altså finna det neste ved å addera 3. Figurtal nr 5 blir då: F₅ = F₄ + 3 = 10 + 3 = 13. Dette er ein såkalt rekursiv formel som er grei å bruka når vi bare skal finna dei neste tala. Men hvis vi feks. skal finna figurtal nr 50, så treng vi ein direkte formel (også kalla eksplisitt) der vi bare kan putta inn n = 50 og rekna ut. Det er som regel dette oppgavene og lærebøkene er opptatt av.

Sidan antalet myntar aukar med 3 for kvar gong, så er det fristande å prøva med formelen F_n = 3n. Men då får vi at F₁ = 3, F₂ = 6, F₃ = 9 osv. Dette passar jo opplagt ikkje. Men når vi ser nøyare etter, ser vi at vi bommar med akkurat 2 kvar gong. Dermed kan vi fiksa dette ved å trekkja frå 2 i formelen.

Vi får då formelen: F_n = 3n - 2.

Denne formelen må passa for alle tala våre, og det er viktig at vi sjekkar. For figurtal 2 får vi F₂ = 3*2 - 2 = 6 - 2 = 4. Så det stemmer. Prøv sjøl og sjå om dei andre stemmer!

Førstegradsformlar

Formelen over er ein førstegradsformel, og det får vi ofte når figuren består av linjer. Førstegradsformlar kan vi bruka når endringen konstant frå ein figur til den neste. Slik er det også med figurane under, som vi kanskje kan kalla "rammetal":

Vi ser at endringen er 4 for kvar gong. Det betyr at vi kan prøva oss med formelen R_n = 4n. Og i motsetning til i stad, så traff vi faktisk med ein gong no! Den generelle regelen for figurtal med konstant endring er F_n = an+ b, der a og b er konstantar. Dette er den samme formelen vi har for rette linjer: a er endringen og b er det figurtalet vi ville fått for figur nr 0. For rammtala over får vi b = 0, fordi hvis vi trekk frå 4 frå figurtal 1, så får vi 0. (For den første figuren er endringen 3, slik at b = F₀ = F₁ - 3 = 1 - 3 = -2. )

Prøv sjøl å finna formelen for figurane under: (her tel vi antal fyrstikker)

Andregradsformlar

Men ofte er ikkje endringen mellom to påfølgande tal ein konstant. Hvis figuren består av utftylte flater, så endar vi ofte opp med ein andregradsformel. Vi skal sjå på noken eksempel.

Kvadrattal

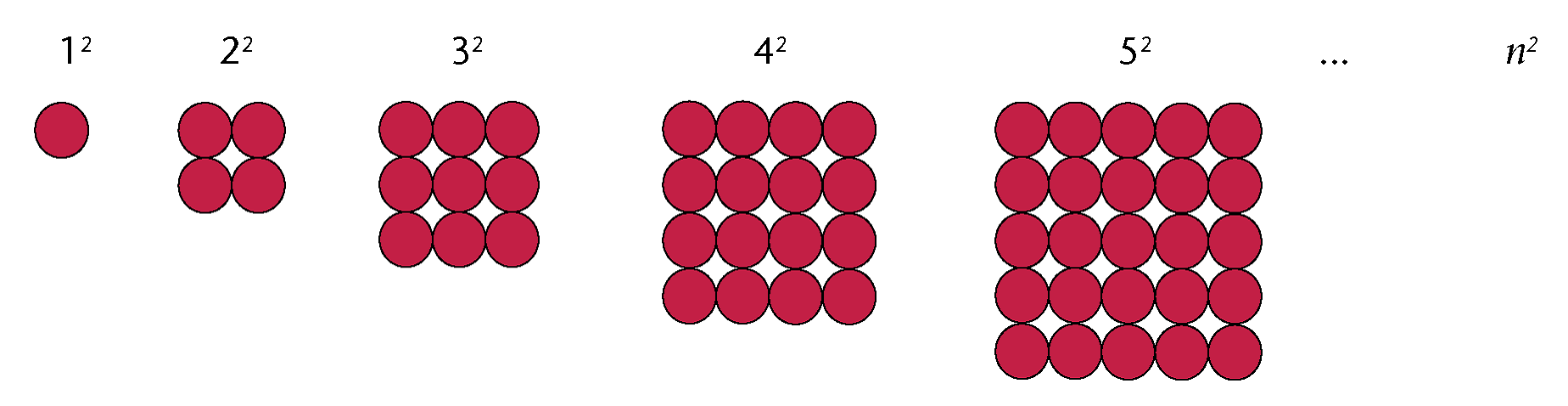
Kvar figur er her eit kvadrat og antallet kuler både i høyde og bredde er lik n. Kvadrattal nummer fem er derfor lik K_n = 5². Dermed forstår vi at den generelle formelen for det n-te kvadrattaler er K_n = n².

Rektangeltal

Trikset for å finna formelen er ofte å leita etter n i figuren. Eksempel er det vi kan kalla rektangeltal. Her tel vi antal kvadrater i staden for prikkar, men ellers er prinsippet det same.

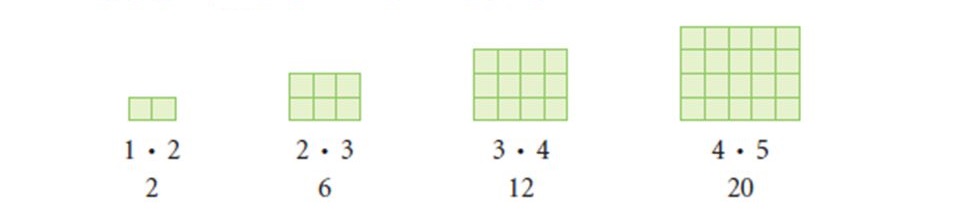
Hvis ser på rektangeltal nummer 3, så ser vi at den består av 3 x 4 kvadrater. Her er n = 3, og vi finn igjen talet som høyden av rektangelet. Bredden er ein meir, dvs n + 1. Antalet kvadrater i figur nr n blir dermed R_n = n(n + 1). Her er det verdt å merkja seg at vi kan danna oss fleire ulike former for rektangeltal, avhengig av korleis figurane ser ut. Så les oppgava nøye!

Trekanttal

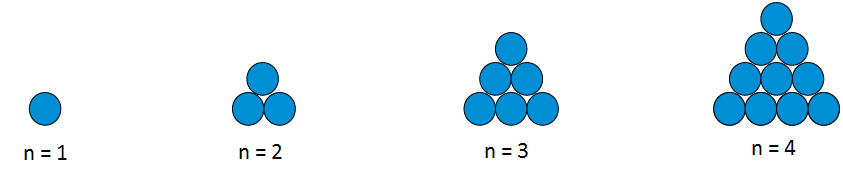
Slik figurane er tegna her, så er det ikkje så lett å sjå kva formelen blir. Men hvis vi tegnar dei på ein litt annan måte, så blir det lettare:

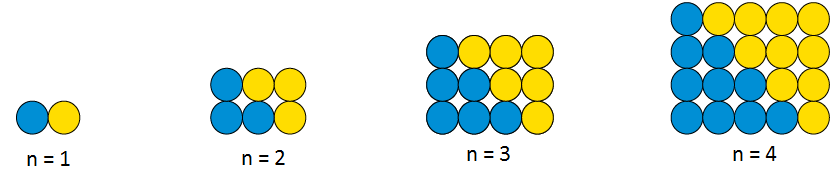
No kan vi sjå at denne trekanten er halvparten av eit rektangel med høyde lik n og bredde lik n + 1. Firkant nummer 4 har feks. høyde 4 og bredde 5. Dermed kan vi bruka samme formel som over, og dela på to. 

Så formelen vår blir:

Samansette figurar

Noken oppgaver blir enklare å løysa ved å dela figurane opp i mindre deler som er kjente. Ved hjelp av dei formlane vi har funne over for kvadrater og rektangel, så er det ikkje så vanskelig å finna ein formel for figuren under, som vi kan kalla "Mikke Mus-figurar":

Systemet er kanskje tydeligast i figur 3. Her har vi eit "hode" som er eit rektangel med høyde 3 og bredde lik 4. Så har vi to "øyrer" som er kvadrater med sider lik 2, altså ein mindre enn n (= 3). Så hvis du bruker kvadratformelen med side (n - 1), og rektangelformelen med sider lik n og n + 1, så kjem du fram. Men husk at det er to "øyrer"!

Formelen blir M_n = 3n² - 3n +2

Tredjegradsformlar

Det hender også at tredjegradsformlar dukker opp. Det kan vi få når vi fyller ut tredimensjonale figurar. Det blir omtrent som å rekna volum.

Kuben

Den enklaste figuren å rekna på er kuben:

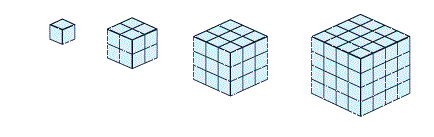
Med same tankegang som for kvadratet, så legg vi merke til at antal småklossar i figur nr 4 er lik 4 x 4 x 4 = 64, sidan det er fire både i bredde, lengde og høyde. Derfor kan vi sei at antalet i kube nr n, er K_n = n³.

Pyramidetal

Figurane under er pyramider med kvadratisk grunnflate.

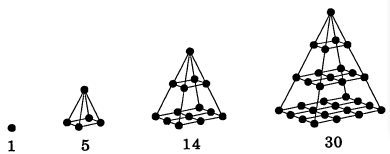
Det viser seg at formelen for pyramideral nummer n, er 

Å finna denne formelen er vel over kanten av det som blir forlangt i 2P. (Bevis her) Men du skal kunna setja inn n, og sjekka at du får tala over. Du kan også prøva ein kalkulator for å finna pyramidetala her.

Utrekning med regresjon

Hvis oppgaven er gitt i del 2, så kan du bruka regresjonsverktøyet i GeoGebra. Hvis vi vender tilbake til "Mikke Mus-tala", så kan vi setja opp følgande tabell i GeoGebra (Trykk "vis regnark"):

Her er n i første rad, og M_n i andre rad. No kan vi bruka regresjonsverktøyet. Vi veit at dette skal bli ein andregradsformel. Derfor velger vi "Polynom" som regresjonsmodell, og "2" i den andre menyen, som står for grad.

Som vi ser, får vi den samme formelen som over, bare med "x" i staden for "n". Husk at den kurven du får opp må treffa alle punkta dine. Her må vi ofte prøva oss litt fram. Hvis du trur at formelen du skal fram til er ein førstegradsformel, så velg "Lineær" for regresjonsmodell. Hvis ikkje den passar, så prøver du polynom. Så prøver du deg fram med grad lik 2, og evt vidare. (Eg har aldri sett oppgaver med grad høgare enn 3). Den modellen med lavast grad som passar alle punkta er den riktige!