Tolegemeproblemet
Tolegemeproblemet handlar om korleis to objekt (som kan vera planeter, stjerner, asteroidar osv.) beveger seg når dei er under påvirkning av ei (gjensidig) gravitasjonskraft. Dette er eit problem som er godt studert, forstått og løyst i alle variantar. På same måten som i det ein kan kalla eit-legemeproblemet (ei planet rundt ei ubevegelig sol, dvs. med uendelig masse), så vil dei to bevega seg i ellipseforma banar (eller hyperbel- / parabelbanar hvis dei har stor nok energi). Men til forskjell frå eit-legemeproblemet, der sola er i eit av ellipsens to brennpunkt, så vil no dei to objekta gå i ellipsebanar der deira felles massesenter er i eit brennpunkt. Men kva betyr egentlig dette?
Massesenteret (barysenteret)
Massesenteret er eit punkt der vi kan tenkja oss at heile massen til eit system er samla, dvs. det same som tyngdepunktet. Når du held ein gjenstand vil du kunna balansera den i dette punktet. Massesenteret til ein hammar er veldig nært hodet fordi det er ein god del tyngre enn skaftet:

Slik er det også med planeter. Tenk deg to planeter festa på ei (uendelig lett og uendelig sterk) stang. Då vil også dette systemet balansera i massesenteret, eller det som astronomane ofte kallar barysenteret.
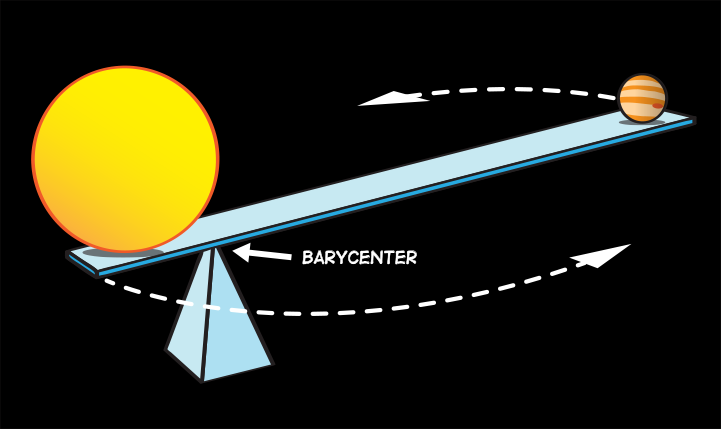
Kor er massesenteret?
Avstanden frå objekt 1 (normalt den tyngste planeten, dvs. ofte sola) til massesenteret er gitt ved formelen:
der :
r1 er avstanden frå objekt 1 til
massesenteret
a er avstanden mellom sentruma av dei to objekta
m1 and m2 er massane til dei to
objekta.
Då forstår vi at jo mindre m2 er i forhold til m1, jo nærmare vil massesenteret vera objekt 1.
Eksempel
Du kan sjøl setja inn massane for sola (1,989E30 kg) og dei andre planetane, og rekna ut. Det vi finn er for eksempel:
- I jord-sol systemet er barysenteret bare 449 km frå sentrum av sola. Når vi samanliknar det med radien til sola, som er 695 508 km, så forstår vi at i praksis så går sola i bane rundt sola. (avstanden til barysenteret er under 1/1000 av radien til sola.)
- Jord - måne: her ligg barysenteret omkring 1,710 km under jordens overflate. Radien til jorda er 6 371 km.
- Jupiter-sol-systemet: her ligg barysenteret 742,000 km frå sentrum av sola, med andre ord rett utanfor sola si overflate. Sjå figur under:
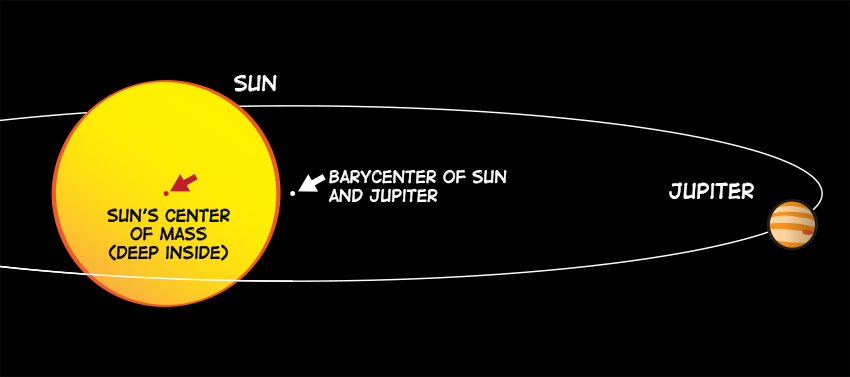
Bevegelse
Hvis vi fortset vårt tankeeksperiment med dei to planetane på ei stang, og antar at planetane er frie til å gli langs stanga, enten innover eller utover - kva vil då skje hvis vi set stanga i rotasjon? Svaret er at det er avhengig av kor fort den roterer. For husk at planetene alltid vil føla ein kraft mot kvarandre, og det er gravitasjonskrafta. Så hvis rotasjonen er veldig sakte, vil planetene begynna å bevega seg mot kvarandre. Det som då skjer er det same som når du beveger deg inn mot midten i ein karusell som roterer fritt; farten aukar! Eit anna eksempel er hvis du sit på ein roterande stol og trekkjer til deg bein og armar. Det motsette vil skje dersom rotasjonsfarten er veldig stor. Då er ikkje gravitasjonskrafta stor nok til å halda dei saman, og dei vil derfor bevega seg frå kvarandre. Resultatet er at rotasjonen vil gå saktare.
Sirkelbanar:
Hvis du no tenkjer at det må finnast ein rotasjonshastighet der planetene sin "trang" til å bevega seg mot kvarandre, akkurat blir balansert av rotasjonen, så stemmer det! Med den akkurat riktige rotasjonshastigheten vil avstanden frå kva planet til massesenteret vera konstant, og dei to planetane vil dermed gå i sirkelbanar rundt massesenteret. Dette ser slik ut:
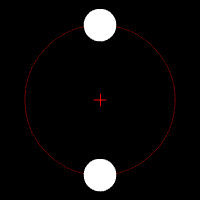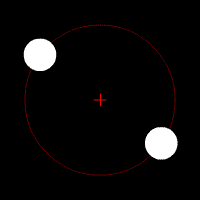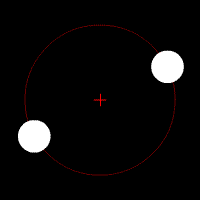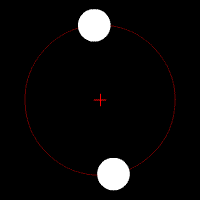

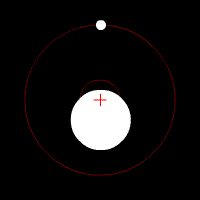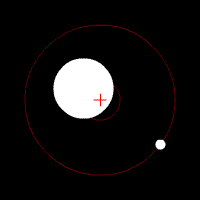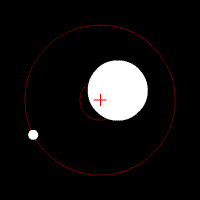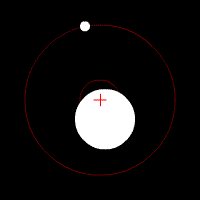
I eksempelet til venstre er dei to planetene akkurat like store, og derfor vil dei ha same avstand til massesenteret. Med andre ord, dei vil gå i akkurat den same sirkelbanen. I eksempelet i midten har dei ulik masse, og går i ulike banar. I eksempelet til høgre er massane så forskjellige at barysenteret er litt innanfor radien til den store massen, slik det er i jord-måne-systemet.
Elliptiske banar
Hvis dei to massane er like, men rotasjonsfarten ikkje balanserer krafta, så vil dei to gå i kvar sin ellipsebane. (Dette forutset at dei ikkje har for stor fart, for då vil dei fly frå kvarandre). Disse ellisane er like store, men snudd kvar sin vei slik figuren under viser. På kvart tidspunkt er dei like langt frå barysenteret, men på kvar si side. Og dei beveger seg inn og ut på den tenkte stanga som roterer om senteret. Det vil sjå omlag* slik ut:
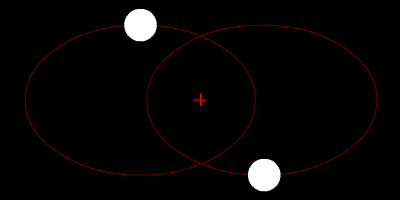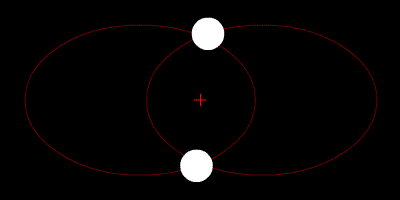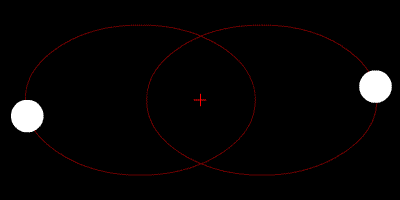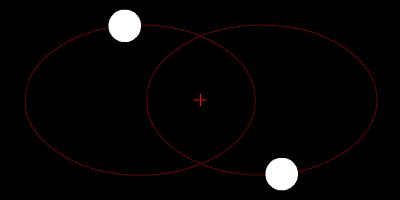
* Eg skriv "omlag" fordi banefarten til dei to planetane vil vera merkbart større nær massesenteret enn lenger ute. Sjå Keplers lover.
Generelt
Hvis massane er ulike, og rotasjonsfarten heller ikkje er balanser kreftene, så vil planetane gå i kvar sin ellipsebane, som ikkje er like. Det kan sjå slik ut (her er barysenteret markert med rødt kryss) :
Sjå simulering av dette.
Bevegelsen til massesenteret
Til no har vi bare antatt at massesenteret står i ro, og det er ikkje nødvendigvis tilfellet. Men vi kan alltid konstruera oss eit koordinatsystem der massesenteret er i ro. Dette vil svara til at vi filmar med eit kamera som for flytter seg med massesenteret (dvs i same fart og retning). Då vil dei banane som kameraet observerer svara til det vi har beskrive over. Når vi bare diskuterer to objekt, så vil ikkje systemet av disse to objekta vera påvirka av ytre krefter. Det vil sei at massesenteret enten vil stå i ro, eller bevega seg med konstant hastighet. Hvis det siste er tilfellet, så vil vi kunna finna posisjonen og farten til dei to objekta når vi kjenner farten til massesenteret, og korleis dei to objekta beveger seg i forhold til kvarandre.Dobbeltsystem
Når barysenteret til to objekt er utanfor begge objekta, så snakkar ein ofte om dobbeltsystem eller binære system. Eit eksempel på dette er systemet Pluto og Charon. Bildet under er tatt av romsonden New Horizons då den var omkring 6 millionar kilometer frå Pluto og Charon, den 8 Juli, 2015. Credits: NASA-JHUAPL-SWRI

Charon er omtrent halvaparten så stor som Pluto, og har dermed (når ein antar same massetetthet) ein åttedel av massen til Pluto. Det skulle då bety at barysenteret er ca. ein nidel av avstanden mellom dei to, frå Pluto. Her er ein animasjon frå NASA som viser dette: (kjelde: APL/New Horizons GeoViz).
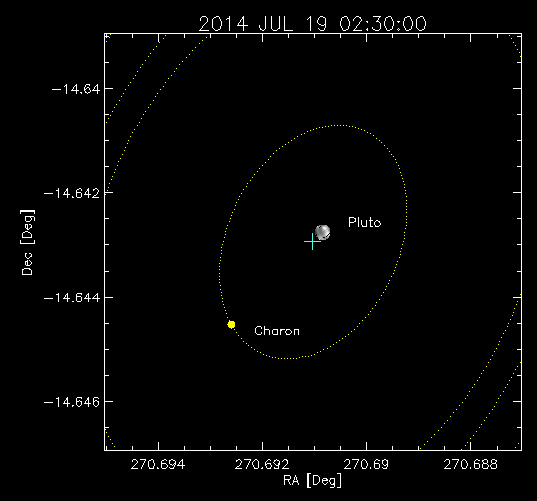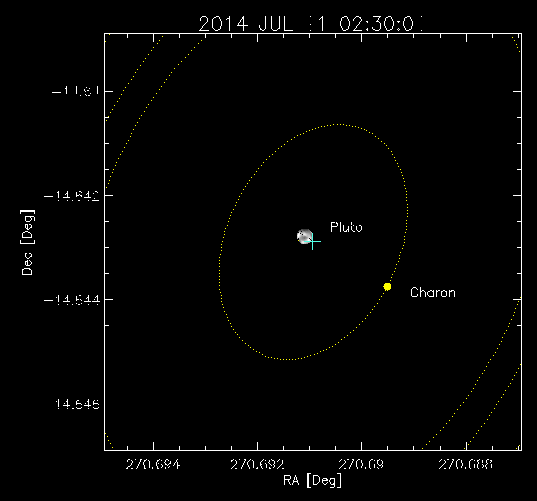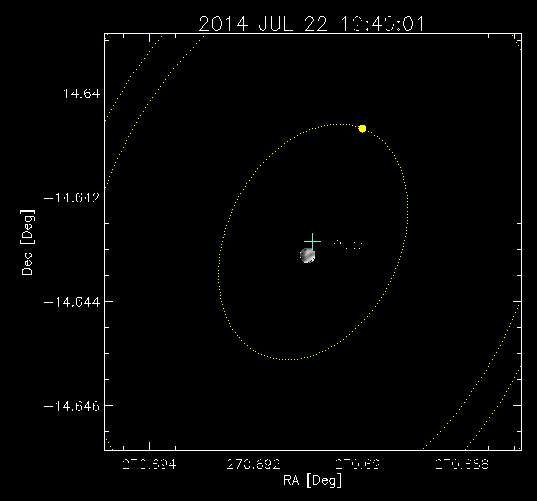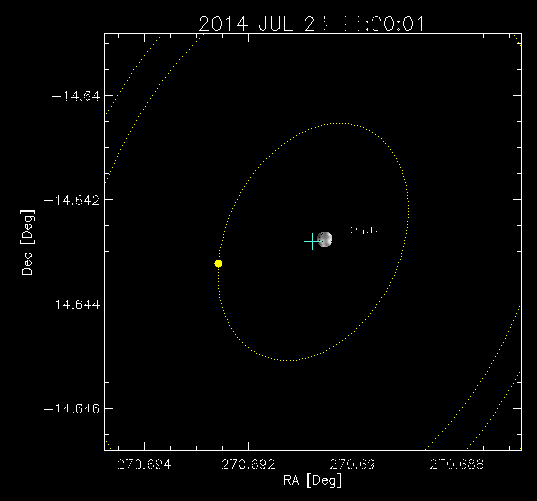
Eit anna eksempel på dobbeltsystem er såkalte dobbeltstjerner. Meir enn fire femtedeler av dei lyspunkta vi ser på himmelen skal faktisk vera system med to eller fleire stjerner. Men spørsmålet er korleis banen til ei planet i eit solsystem med to soler er, kan du lesa meir om i artikkelen om trelegemeproblem.
