Numerisk derivasjon
Når vi har kjennskap til funksjonsuttrykket til ein funksjon, kan vi derivera på vanlig måte (dvs. analytisk). Men når vi ikkje kjenner uttrykket må vi ty til numerisk derivasjon. Vi tar likevel utgangspunkt i definisjonen av den deriverte av ein funksjon \(f(x)\). Vi lar \(x\) få eit lite tillegg \(h\) (ofte kalla \(Δx)\) og finn stigningstalet til linja gjennom dei to punkta \((x, f(x))\) og \((x+h,f(x+h))\).
Når vi finn grenseverdien for dette stigningstalet når \(h\) går mot null, så har vi definisjonen av den deriverte:
\[ f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h } \right) - f\left( x \right)}}{h } \]
Newtons kvotient
Denne definisjonen er nyttig for å finna analytiske uttrykk for den deriverte. Hvis vi kjenner funksjonsuttrykket kan vi derivera for hånd og finna den deriverte på den måten. Men no skal vi gjera det numerisk. Då kan vi ikkje la \(h\) bli null for då får vi divisjon med null. Men vi kan finna ein tilnærming ved å bruka ein liten \(h\):
\[ f'(x) \approx \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h } \]Denne tilnærminga blir kalla Newtons kvotient.
Optimal h-verdi
Spørsmålet er kor liten verdi kan vi putta inn? Ein skulle tru at det bare var å bruka så liten \(h\) som datamaskinen klarar å rekna med, men det viser seg å vera fullstendig feil. Nedanfor har vi rekna ut den numerisk deriverte for sinus-funksjonen for \(x = 0.5\) vha. Newtons kvotient. Vi veit at den deriverte av \(sin(x)\) er \( cos(x) \), så det kan vi bruka som fasit: \(cos(0.5) = 0.8775825618903728\) Når vi prøver ulike verdiar av \(h\), og reknar ut den deriverte og feilen vi gjer, så der det omtrent* slik ut:
Trunkeringsfeil vs avrundingsfeil.
Ved å bruka ein endelig \(h\) i staden for å la den gå mot null, introduserer vi ein feil. Dette kallast for trunkeringsfeil. Denne typen feil minkar når vi lar \(h\) minka frå \(10^{-1}\). Men til vår overraskelse (?) begynner den totale feilen å auka igjen ved \(h = 10^{-9}\). Grunnen til denne rare oppførselen er at eit flyt-tal bare kan representerast tilnærma i ein datamaskin, fordi vi har bare eit endelig antal siffer å bruka. Dette kallast avrundingsfeil, og det har vi alltid. Men når vi utfører ein divisjon og både teljar og nevnar blir mindre og mindre så begynner avrundingsfeilen å gir større utslag.
* Min kjøring avvik bittelitt frå denne, og det har nok med kva program og / eller kva maskin den er kjørt på, å gjera. Men alt i alt er oppførselen veldig lik.
Newtons symmetriske kvotient
Ein betre tilnæring er Newtons symmetriske kvotient der vi finn stigningstalet til linja gjennom dei to punkta \((x - h, f(x-h)\) og \((x+h,f(x+h)\). Med andre ord går vi eit lite steg \(h\) til venstre og eit tilsvarande steg til høgre. Derfor må vi dividera med \(2h\) for å få stigningstalet:
\[ f'(x) \approx \frac{{f\left( {x + h } \right) - f\left( x - h \right)}}{2h } \]
Figuren under viser at Newtons symmetriske kvotien er nesten parallell med tangenten for denne funksjonen med dette valget av h. Det vil ikkje alltid vera slik, men som regel gir Newtons symmetriske kvotient eit meir korrekt svar.
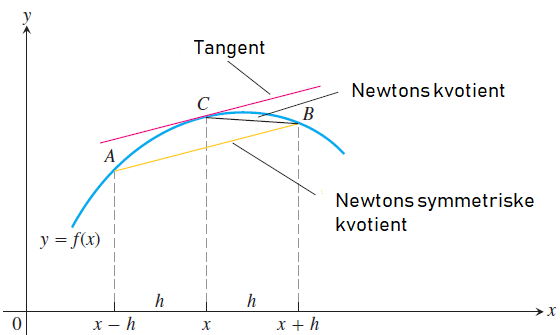
Den minste feilen med denne vart \(7.5 \cdot 10^{-12}\), og det skjedde alt ved \(h = 10^{-6}\).
Fjerdeordens formlar
Det fins også andre formlar som denne, som får feilen ytterligare ned:
\[ f'(x) \approx \frac{{ -f\left( {x + 2h } \right) + 8f\left( {x + h } \right) - 8f\left( x - h \right) + f\left( {x - 2h } \right)}}{12h } \]
Det viser seg at minste feil no blir \(5.8 \cdot 10^{-15}\) for \(h = 0.001\). Så det ser ut til at jo betre metode, jo større \(h\) kan vi klara oss med.