Mekanisk energi i tyngdefeltet

Vi skal studera den mekaniske energien til ein gjenstand med masse m som befinn seg i tyngdefeltet til ein mykje større gjenstand med masse M. Typiske situasjonar er planeter i tyngdefeltet til sola, eller satelittar i tyngdefeltet til jorda. Vi skal bruka satelittbanar som eksempel, men ha i bakhovet at dette gjeld generelt. Men vi gjer ein forenkling ved at vi krever at m << M, dvs. at massen til den sirklande gjenstanden er mykje mindre enn denn som er i "sentrum". Vi ser også bort frå luftmotstand og påvirkning frå andre gjenstandar.

Generell formel

Den mekaniske energien til ein gjenstand som befinn seg i eit tyngdefelt er summen av den kinetiske energien E_k og den potensielle energien E_p, altså, E = E_k + E_p. Dette kan vi uttrykkja som:

E = \frac{1}{2} m v^{2} - G \frac{M m}{r}

,der v er farten til gjenstanden med masse m, G er gravitasjonskonstanten: G= 6,7×10^-11N×m²/kg² og r er avstanden mellom dei to gjenstandane. Merk at den potensielle energien er negativ, men går mot 0 når avstanden r går mot uendelig.

Sirkelbevegelse

I det enklaste tilfellet har vi ein satelitt i sirkelbane med konstant banefart. Då vil den ha ein konstant akselerasjon inn mot sentrum med verdien $a = \frac{v^{2}}{r}$ . Dette kallast sentripetalakselerasjonen. Sidan den einaste krafta som virkar på satelitten vår er gravitasjonskrafta gitt ved Newtons gravitasjonslov: $F = G \frac{M m}{r^{2}}$ . Newtons andre lov gir dermed:

m \frac{v^{2}}{r} = G \frac{M m}{r^{2}}

No kan vi multiplisera med r på begge sider av likningen og dividera med 2, og då får vi eit uttrykk for den kinetiske energien til ein gjenstand i konstant sirkelbevegelse:

\frac{1}{2} m v^{2} = G \frac{M m}{2 r}

Sidan v er konstant, har vi også konstant kinetisk energi. Dette gir eit uttrykk for den totale mekaniske energien for ein uniform sirkelbevegelse:

E = + \frac{G M m}{2 r} - \frac{G M m}{r} = - \frac{G M m}{2 r}

Vi kan også bruka likningen for kinetisk energi over til å finna eit uttrykk for banefarten v:

v = \sqrt{\frac{G M}{r}}

Dette betyr at vi kan rekna ut banefarten i ein sirkelbane når vi kjenner radien r. Denne farten kallast også for sirklingsfarten eller sirklingshastigheten.

Elliptisk bevegelse.

Når ein satelitt bevegar seg i ein elliptisk bane, vil jorda befinna seg i eit av brennpunkta. (M på figuren). Viktige begrep: Perigeum er punktet med kortast avstand (r_p) til jorda, og apogeum er punktet med lengst avstand (r_a). Avstanden mellom Perigeum og Apogeum kallast den store aksen. Halve denne er kalla store halvakse (a).

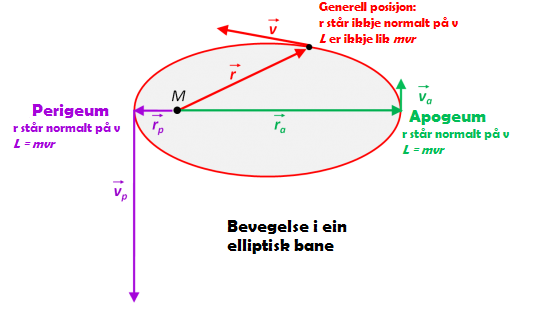
No tar vi utgangspunkt i vår første likning over, og multipliserer med r². I dei to ekstremalpunkta, perigeum og apogeum, vil fartsvektoren v stå normalt på r-vektoren. Det betyr at i disse punkta kan det angulære momentet skrivast som L = mvx. Dermed får vi følgande likning:

E r_{e x}^{2} = \frac{1}{2} m v_{e x}^{2} r_{e x}^{2} - G M m r_{e x} = \frac{L^{2}}{2 m} - G M m r_{e x}

der indeksen "ex" står for enten apogeum eller perigeum. Det kan visast at angulære momentet er konstant (bevart) i denne bevegelsen. Så hvis vi flytter over leddet GMmr_ex til venstre side, så blir høgre side konstant. Det betyr at uttrykket vi får på venstre side blir det same i apogeum, og perigeum:

E r_{a}^{2} + G M m r_{a} = E r_{p}^{2} + G M m r_{p}

Løyser vi denne likninga med hensyn på E, får vi:

E = \frac{G M m (r_{p} - r_{a})}{r_{a}^{2} - r_{p}^{2}} = - \frac{G M m}{r_{a} + r_{p}}

Frå figuren ser vi at r_a + r_b er lik heile store aksen i ellipsen, eller med andre ord lik 2a, der a er store halvakse. Då kan vi altså skriva dette som:

E = - \frac{G M m}{2 a}

Vis-viva likningen

For ein gjenstand i ellipsebane har vi altså at den totale mekaniske energien er gitt ved:

E = \frac{m v^{2}}{2} - \frac{G M m}{r} = \frac{- G M m}{2 a} .

Hvis vi løyser denne likninga mhp. v, får vi:

v^{2} = μ (\frac{2}{r} - \frac{1}{a}),

der vi har definert den standard gravitasjonelle parameteren

μ = G M.

Dette er den såkalte vis-viva likningen, og er det analoge uttrykket til formelen for v i ein sirkelbane over, bare at her er den samanhengen gitt ved v².
Dette betyr at når vi kjenner store halvakse, så kan vi finna banefarten i eit gitt punkt i banen (der r er kjent).

Diskusjon

Merk følgande:

Mens både den kinetiske og potensielle energien i ein sirkelbane er konstant, så vil begge disse variera gjennom eit omløp i ein ellipsebane. I perigeum er den kinetiske energien størst og den potensielle minst, og i apogeum er det omvendt. På vei frå apogeum til perigeum vil tyngdekraften utføra eit positivt arbeid på gjenstanden. Det betyr at den kinetiske energien vil auka, sidan det ikkje er andre krefter som virkar. Samtidig blir avstanden til den sentrale masse mindre, og det betyr at den potensielle energien minkar.
Summen av E_k og E_p, dvs. den totale mekaniske energien E, er likevel konstant i den elliptiske banen, slik det er i den sirkulære.
Når ellipsen degenerer til ein sirkel, så har vi at a = r. Då vil både likningen for mekanisk energi E, og likningen for omløpsfarten v, til ein gjenstand i elliptisk bane blir lik dei som gjeld for ein sirkel. Slik må det jo vera, men her ser vi det eksplisitt.
Når ellipsen blir uendelig stor, dvs når a går mot uendelig, så vil gjenstanden i apogeum i praksis vera fri frå tyngdefeltet til den store massen M. Når a går mot uendelig får vi $v_{e} = \sqrt{\frac{2 G M}{r}},$ Dette er det same som unnslipningshastigheten i avstanden r. Merk at dette er √2 * sirklingsfarten over!

LENKER

Circular orbit.
Conservation of Mechanical Energy in Keplerian Orbits,