Numerisk løysing av differensiallikningar 1¶
Eksempel frå matematikken¶
Den største fordelen med å løysa differensiallikningar numerisk er at vi kan løysa likningar som ikkje går an å løysa på papiret (såkalt analytisk løysingar). Men no vil vi gjerne testa Eulermetoden (Sjå Krasjkurs i Eulermetoden), og derfor vil vi starta med eit eksempel der vi kjenner fasiten, nemlig likninga
$y'(t) = 3t^2$.
Denne likninga kan vi greit løysa ved å integrera (antiderivera) uttrykket på høgre side. Vi finn då den generelle løysinga:
$y(x) = t^3 + C$, der C er ein konstant.
Når vi deriverer y(t), så ser vi at uanset kva verdi C har, så får vi den same deriverte, sidan den deriverte av ein konstant er lik null. Derfor har vi egentlig uendelig mange løysingar på likninga vår. Under viser vi tre av dei, der med C = 1, C = 0 og C = -1:
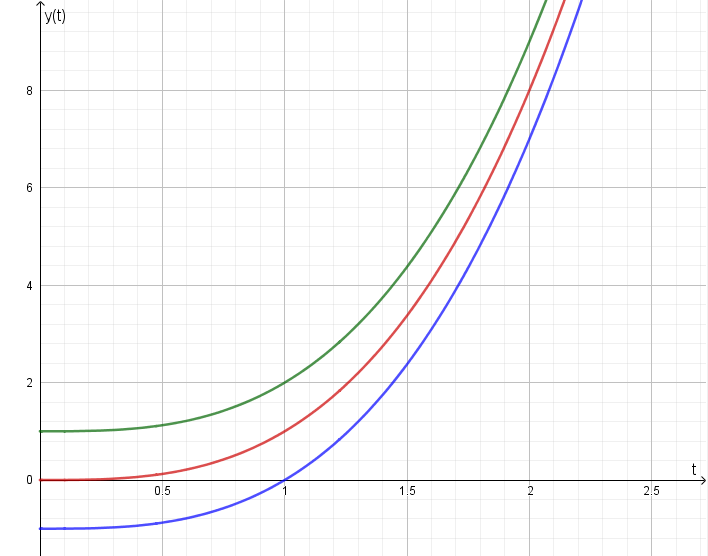
For å bestemma ei bestemt av disse, så treng vi å kjenna eit punkt på grafen. Så la oss sei at vi veit at grafen startar i punktet (0,1). Dette skriv vi som initialbetingelsane ved t = 0:
$t_0 = 0, y(t_0) = 1$
Koden for å løysa likningar blir då:
import numpy as np
import matplotlib.pyplot as plt
def f(t): # Den deriverte er ikkje avhengig av y
return 3*t**2
def analytisk(t): # Fasit
return t**3 + 1
t0 = 0 # Initialbegingelse for t
y0 = 1 # Initialbegingelse for y
N = 20 # Antal intervall
bredde = 2 # Intervallbredde
dt = bredde/(N) # Steglengde
# Arrays. Vi treng et punkt meir enn antal intervall
t = np.zeros(N+1)
y = np.zeros(N+1)
a = np.zeros(N+1)
# Startverdiar
t[0] = t0
y[0] = y0
a[0] = y0
# Eulers metode
for i in range(N):
m = f(t[i])
y[i+1] = y[i] + m*dt
t[i+1] = t[i] + dt
a[i+1] = analytisk(t[i+1])
#Plotting
plt.plot(t,y,label = "Numerisk")
plt.plot(t,a,label = "Analytisk")
plt.legend(loc='best')
plt.xlabel('t')
plt.ylabel('y')
plt.title("'Numerisk løysing av y'(t) = 3t^2")
plt.grid(b=True)
plt.show()
Forklaring¶
Vi har bruk for biblioteket numpy for å kunna bruka funksjonen zeros, som fyller et array med eit antal nullar. I staden for å importera med "from numpy import *", som noken gjer, så skriv vi heller "import numpy as np". Grunnen er at då blir det tydeligare i koden når vi bruker numpy. Vi må skriva "np.zeros", som er litt meir skriving, men tydeligare. Vi gjer det på same måten med matplotlib.pyplot, som får kortnavnet plt. Dette er rekna som den beste måten å importare bibliotek.
Så definerer vi f(t) som er funksjonen for y'(t). Til vanlig er denne ein funksjon både av t og y, men i dette tilfellet blir treng vi bare t. Vi definerer også ein funksjon som gir oss fasiten.
Oppgaver¶
- Varier N, og sjå korleis den numeriske løysinga endrar seg.
- Løys likninga $y'(t) = yt + t^3$ med same initialbetingelsar som over. Løysinga er $y(t) = 3e^{t^2/2} - t^2 -2$
- Prøv no på likninga $y'(t) = y/t + 1$, som har løysinga $y(t) = t \cdot ln(0.5t)$. Her kan vi ikkje starta med t = 0, for då får vi null i nevnar. Så vi startar heller (for eksempel) i t = 0.001, og då blir $y = 0.001\cdot ln(0.0005)$.
- Løys likninga $y'(t) = sin(t) + t \cdot cos(t)$ med initialbetingelsane y(0) = 0. Her er fasiten $y(t) = t \cdot sin(t)$