Differensiallikningar og metodar for å løysa disse er eit veldig stort tema. Men det du treng vita i dette kurset er:
Ei differensiallikning er ei likning som inneheld den deriverte (av første og/eller høgare grad) av ein funksjon. Den inneheld ofte også funksjonen sjøl og eit uttrykk med den uavhengige variabelen. Eksempel på dette kan vera y' = x + y2, y' + 4y + 3x = 0, y'' = -3y osv. I dei to første er den uavhengige variabelen tydeligvis x, slik at løysinga er ein funksjon y(x), mens i den siste er ikkje det nødvendigvis slik. Her kan løysinga like godt vera ein funksjon y(t). Slik er det som regel i fysikken, der vi er ute etter å beskriva korleis ein variabel varierer med tida, som feks farten, v(t) og akselerasjonen a(t). Ofte er difflikningane i mekanikken ikkje skrivne ekplisitt. Likningar med Newtons andre lov er derfor i realiteten difflikningar, sidan vi kan skriva akselerasjonen som den dobbeltderiverte av posisjonen. Hvis objektet vårt beveger seg i horisontal retning og summen av kreftene er F, så kan vi skriva Newtons andre lov som F = ma, men vi kan også skriva den om som F = mx''. Då er vi ute etter å finna funksjonen x(t).
Vi ser også at den siste likninga innheldt den andrederiverte y'' av funksjonen, så dette er derfor ein andreordens difflikning, mens dei to første er førsteordens. Vi kjem bare til å jobba med difflikningar der funksjonen er av ein variabel. Dette kallast for ordinære difflikningar. (På engels ser vi ofte brukt ODE, dvs Ordinary Differential Equations)
For å testa om ein funksjon er ei løysing på difflikninga vår, gjer vi som vi pleier med vanlige likningar: vi set inn løysinga og reknar ut venstre og høgre side, og sjekkar om dei er like. Forskjellen her er at vi set inn ein funksjon, og då får vi funksjonsuttrykk på begge sider, mens i vanlige likningar får vi tal. Eksempel: Hvis ein gjenstand beveger seg vertikalt i tyngdefeltet under fritt fall (ingen luftmotstand), så har vi at G = ma, eller mg = ma, dvs a = g. (tyngdeakselerasjonen). Det blir då difflikninga y'' = g. Hvis vi forenklar dette og set g = 10, så påstår eg at løysinga blir y(t) = y0 + v0*t + 5*t2, der y0 og v0 er konstantar. La oss sjekka om dette stemmer: Vi deriverer funksjonen og får y'(t) = v0 + 10t. Når vi huskar at v'(t) er det same som v(t), så kjenner vi gjen fartsformelen for konstant akselerasjon: v = v0 + at. Så deriverer vi ein gong til og får y''(t) = 10. Så dette stemmer.
Løysinga vår over har to ubestemte konstantar y0 og v0. Her er y0 lik startposisjonen y(0), og v0 er startfarten v(0), eller y'(0). Når vi løyser difflikningar får vi alltid minst ein ubestemt konstant, som må oppgiast for at vi skal finna ei bestemt løysing. Dette kallast for initialbetingelsane. I fysikkoppgaver ser vi ofte at y0 stilltiande blir sett til 0, dvs at bevegelsen startar i origo. Då forenklar løysinga vår seg til ei likning som mange gonger blir skriven som s = v0t + 1/2 at2. Vi kjenner dette igjen som ei av bevegelseslikningane for konstant akselerasjon.
I eksempelet over fekk vi to ubestemte konstantar, og det var fordi likninga vi hadde var av andre orden. Så når vi deriverte første gong, forsvant y0, og når vi deriverte ein gong til, så forsvant v0. Førsteordenlikningar gir bare ein ubestemt konstant, så hvis vi for eksempel har ei likning y' = 3t2, så kan initialbetingelsen for eksempel vera at y(0) = 1. Då vil løysinga y(t) = t3 + 1. Vi skal sjå seinare korleis vi løyser denne numerisk.
Vi skal først sjå korleis vi kan bruka Eulermetoden til å løysa førsteordens difflikningar. Felles for disse er at vi kan omskriva dei som
y' = f(t,y)
La oss sei at vi skal løysa likninga 2y' - 4y + 6x = 0. Då kan vi skriva den om som y' = 2y - 6x. Då blir f(x,y) = 2y - 6x. Funksjonen f er altså ikkje den som vi skal finna (for denne er i dette eksempelet y(t)), men bare eit navn vi gir det uttrykk som gir oss den deriverte av y(t) i eit gitt punkt. Som vi veit, er y'(t) det same som stigningstalet til tangenten i punktet, og det skal vi bruka nedanfor til å finna ein metode for å estimera funksjonen y(t) punktvis.
Den grøne kurven på figuren er grafen til den funksjonen y(t) som vi prøver å estimera. Vi tar då utgangspunkt difflikninga og initalbetingelsane. La oss sei at vi kjenner punktet P0 = (t0, y(t0)). Her kan vi rekna ut den deriverte vha. funksjonen vår: y'(t0) = f(t0, y0). Og dette talet bruker vi no til å finna eit nytt punkt (x1, y1) som vi håper ligg nær kurven. Ettpunktformelen gir då at y1 - y0 = f(t0, y0) * (t1 - t0). Når vi omdøper differansen (t1 - t0) = ∆t, så kan vi flytta over y0, og få formelen y1 = y0 + ∆t f(t0,y0).
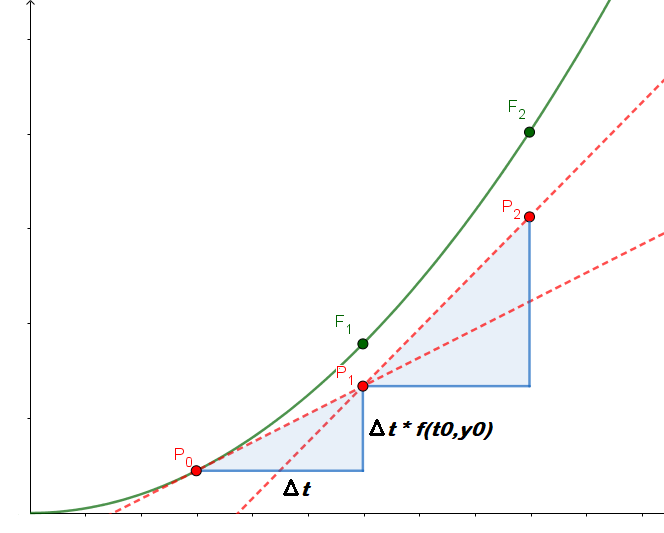
No kan vi gjenta dette, og finna det neste punktet P2 ved å bytta ut indeksen 0 med 1, og 1 med 2. Då får vi ein tilsvarande formel:
y2 = y1 + ∆t f(t1,y1)
Dette kan vi bruka iterativt. Vi bruker dei estimerte verdiane frå eit punkt til å finna det neste. Så når vi kjenner den deriverte i punkt Pn, så kan vi rekna ut den neste y-verdien yn+1 ved hjelp av den generell formelen
yn+1 = yn+∆t f(tn,yn)
definer funksjonen f(t,y)
sett t0 og y0 sett steglengda, dt og antalet steg, N
for n frå 1 til N gjer
m=f(tn,yn)
yn+1=yn+ m*dt
tn+1 = tn + dt
plott t,y
Til slutt kan du sjå på eit eksempel der vi løyser likninga y′(t)=3t2. Prøv også oppgavene!
Introduction to DifferentialEquations.
1.7 Numerical methods: Euler's method . Med retningsdiagram
Example: Solving Ordinary Differential Equations (ikkje dum den)
Eksempel. Ikkje alt like relevant
Simulating an ordinary differential equation with SciPy. Kast m luftmotstand
Solve Differential Equations with ODEINT.
Numerical Methods for Ordinary Differential Equations 2nd Edition. (overkill?)
Numerical Methods for Ordinary Differential Equations.(ser meir overkommelig ut)
Solving Ordinary
Differential Equations I. (Virkar litt vanskelig?)
Authors: Hairer, Ernst, Nørsett, Syvert P., Wanner, Gerhard