Bevegelseslikningane

Utledning av bevegelseslikningane for konstant akselerasjon

I: Fartsformelen

Vi skal finna ein formel for farten v ved tida t, og tar utgangspunkt i definisjonen av gjennomsnittsakselerasjon samtidig som vi antar at t₀ = 0. Det betyr at Δt = t. Sagt på ein annan måte: vi antar at gjenstanden vi reknar på har farten v₀ når vi startar klokka.

Når vi plottar dette i ein fartsgraf, kan det sjå slik ut:

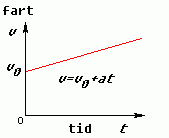
II: Veiformel 1

Her tar vi utgangspunkt i formelen for gjennomsnittsfart. Hvis vi seier at bevegelsen startar i origo når vi startar klokka, så betyr det at s₀ = 0, og t₀ = 0. Då forenklar definisjonen seg til

Når vi veit at vi har konstant akselerasjon, så veit vi at farten stig lineært. Då (og bare då!) kan vi også skriva gjennomsnittsfarten som:

Disse to formlane for gjennomsnittsfart må jo gi samme svar. Så vi set dei lik kvarandre og får:

Denne formelen kan vi tolka grafisk som arealet under fartsgrafen:

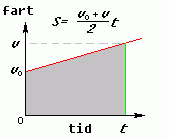
III: Veiformel 2

Når vi set uttrykket for v frå fartsformelen inn i formelen vi nett fant, får vi:

Hvis vi plottar dette i ein veigraf, så kan det sjå slik ut:

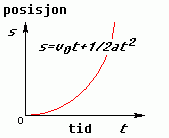
Et spesialtilfelle:

Hvis bevegelsen startar frå ro, dvs. at startfarten v₀ = 0, så gir veiformel 2:

IV: Den tidlause formelen

Hvis vi løyser fartsformelen med hensyn på t får vi:

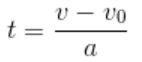
Set vi no dette uttrykket inn for t i veiformel 1 får vi ein ny formel uten t: