

Brooklands-banen var bygd med sement, og etter kvart som den vart dårligare kunne det bli ein humpete tur.
Grovt sett kan vi tegna kreftene som virkar i fartsretningen og vertikalt på ein bil slik:
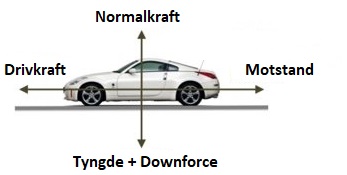
Krefter i fartsretningen: Framover virkar det vi kan kalla drivkrafta
eller motorkrafta, og bakover virkar motstanden, dvs. rullemotstand og luftmotstand.
Krefter i vertikal retning: Nedover virkar tyngdekrafta pluss evt. den
såkalte "Downforce" (sjå nedanfor) og Normalkrafta
(summen av kreftene frå bakken på hjula)
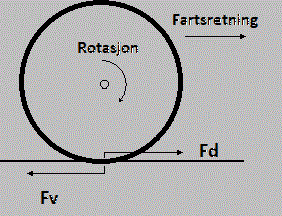
Når bilen bruker motorkraft for å få framdrift, virkar motoren på dekka via drivlinja. På bildet under går bilen til høgre, og motoren får hjula til å rotera med klokka. Då vil dekka virka med ei kraft Fv bakover (dvs. mot venstre) på bakken. Motkrafta til denne er krafta frå bakken på dekket Fd. Denne krafta virkar framover. Det er denne som driv bilen framover! Også Fd er ei statisk friksjonskraft så lenge hjulet ikkje spinn. Ved bremsing vil retningane på Fv og Fd vera motsatt.
Under ser vi kreftene på ein bil som svingar til venstre. Når ein bil eller ein annan gjenstand svingar så er den akselerert innover i svingen. Det kallast sentripetalakselerasjonen, som er gitt som v2/r. Det betyr at kraftsummen på bilen må virka innover. Dette er eit resultat av at bakken virkar med ei friksjonskraft på dekka (og dermed på bilen). Denne krafta er retta innover i svingen, og er egentlig ei statisk friksjonskraft, så lenge dekka ikkje sklir. Les meir om sirkelbevegelse.
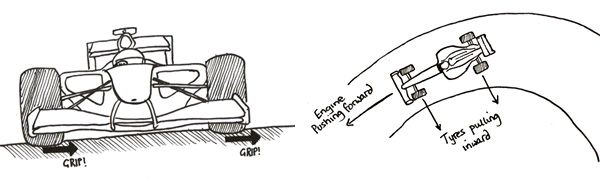
Hvis ein bil mister heile veigrepet, vil den begynna å skli. og fortsetja rett fram, og det vil vi jo sjølsagt unngå! Spørsmålet er korleis. De er altså friksjonskrafta mellom bakke og hjul som held bilen inne i svingen. Den maksimale friksjonskrafta er gitt som Rmax = µsN, der µs er den maksimale friksjonskoeffisienten mellom bakke og dekk, og N er normalkrafta frå bakken og opp mot bilen.
Oppsummert kan ein sei at:
Ein racingsjåfør vil naturligvis ha så stor v (dvs fart) som mulig. Og banen er jo gitt, så då skulle ein tru at radien for kvar sving også var gitt. Ein skulle tru at den beste linja gjennom ein sving ville vera å kjøra ein så vid sirkelbue gjennom svingen som mulig, og derved gjera r så stor som mulig. Dette er den stipla linja på figuren under. Med denne strategien vil ein kunna halda ein konstant fart gjennom svingen som er relativt høg. Men dei fleste sjåførar ynskjer å begynna svingen litt seinare (raud linje). Dei må då bremsa kraftigare og får då ein litt brattare og tregare første del av svingen, men kan akselerera ut av svingen fordi dei får ein mindre bratt sving i siste del. Men denne måten å gjera det på foruset jo at du har gode nok bremser og akselerasjon, Dessuten vil den beste linja også vera avhengig av korleis banen ser ut etter svingen. Så her er det mange variable å ta hensyn til.
For å auka friksjonen kan ein auka friksjonskoeffisienten mellom dekk og vei. Dette koker ned til betre dekk. Vanlige bildekk har kanskje ein friksjonskoeffisient på godt under 1, men racingdekk er som oftast uten mønster og kan ha ein friksjonskoeffisient på tørr asfalt på 1.8! (vanskelig å få gode tal), mens på våt bane kan det same dekket komma ned i 0.1 Så det å finna det rette dekket til den rette bilen på den rette banen er ein blanding av kunst, vitenskap og big bisniss. Racindekk oppfører seg ikkje akkuat slik som skulefysikken tilseier mhp. friksjon. For eksempel er friksjonen avhengig av kor stor kontaktflata mot bakken er, og derfor er racingdekk ekstra breie. Heller ikkje teorien om at glidefriksjon vs statisk friksjon stemmer heilt, ser det ut til. Denne kjelda hevdar at veigrepet er størst når det er ørlite skrens. Om det er korrekt eller ikkje, så er det uansett akkurat på denne grensa ein racingsjåfør må halda seg heile tida, for å vinna løp.
Men sjøl om grensene blir pusha, så har alle dekk sine grenser for yteevne. Den andre muligheten er å auka friksjonen er å auka N. Ein måte er å gjera bilen tyngre. Men det ville resultert i tregare akselerasjon og like store problemer som før, fordi dei kreftene som trengs for å halda bilen på plass i svingen, eller for å akselerera eller bremsa den vil bli tilsvarande større. Normalt vil ein ha ein lett bil. Ein betre mulighet er då å auka marktrykket ved å endra på bilens form. Ein bruker det same prinsippet som skaper løft i flyvinger, men snur dei oppned slik at trykket blir nedover. Dette kan gjerast både gjennom bilens generelle form og gjennom påmonterte vinger. Opp gjennom historien er det gjort mykje prøving og feiling gjennom å laga vinger, foilar osv. Dagens Formel 1-bilar er i stand til å skapa eit trykk nedover på 6 G, dvs. seks gonger sin egen vekt! Ein bivirkning av dette er at bilen får meir luftmotstand. Men på banar med mange svingar er det likevel veldig lønnsomt å kunna ha høg fart i svingane, sjøl om du taper ein del på langsidene. Dagens Formel 1-bilar kjører så fort i svingane at sjåførame må gjera spesielle styrkeøvelsar for nakken.

Noken banar er utstyrt med doserte svingar. Det betyr at veibanen hellar innover. I ein slik sving vil normalkrafta virka på skrå innover, og vi kan dekomponera den i ein vertikal komponent Ny = N cos θ og ein horisontal komponent Nx = N sin θ. I eksempelet under kjører bilen i ein bane med null friksjon. Det vil sei at det er ingen krefter frå bakken på hjula som kan hjelpa bilen i å halda banen. Så all kraft vertikalt er Nx. Det betyr at dette er lik sentripetalkrafta. Hvis vi forutset at bilen held seg i banen, kan vi altså setja at Nx = m v2/r. Dermed kan sjåføren klara svingen hvis han / ho justerer farten slik at den passar i likninga. Hvis den er litt for stor vil bilen skli oppover og utover i svingen, og motsatt hvis den er for liten. Det kan jo vera ein grei oppgave å finna denne farten!
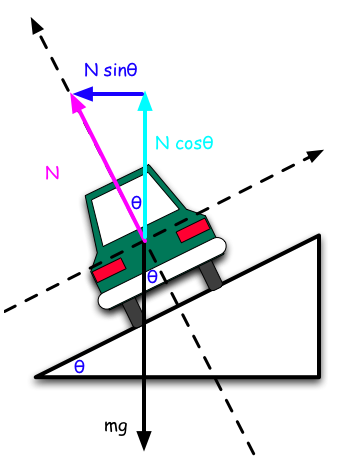
Dette med null friksjon er jo eit tenkt eksempel. I praksis vil det vera både friksjonskrefter og horisontalkrafta Nx som virkar innover i svingen. Men det betyr at bilen kan kjøra fortare i svingen uten å mista veigrepet i ein dosert sving, enn i ein flat. Og det er jo heile poenget med doseringa.
Men heller ikkje dette er bare, bare. Den første doserte banen var Brooklands motor circuit. Den hadde dosering på 30 grader og skal ha forårsake minst 17 dødsfall, inkludert tre uheldige tilskuarar og to mekanikarar. Korfor? Fordi det var ikkje gjerde rundt, og dei bilane som då ikkje klarte svingen datt ni meter ned på utsida. På italienske banar som Monza og andre europeiske banar gjekk doseringar etter kvart ut av bruk, mens ein i USA fremdeles har sine kjedelige NASCAR løp på banar som har doseringar på opptil 36 grader.
Uansett kor god banen er, og kor gode dekka er, så har vi sett at det er grenser for kor fort ein bil kan kjøra gjennom ein gitt kurve. Det betyr at bilen må bremsa ned til maks hastighet før svingen, og akselerera så mykje den kan på rettstrekkene. Så dagens racingbilar har ekstreme akselerasjons- og bremse-egenskaper. Men dette skaper også problemer som vi skal sjå litt på.
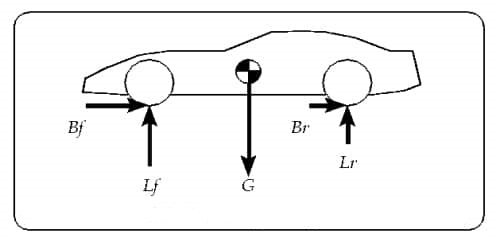
Når ein bil bremsar oppstår eit dreiemoment om tyngdepunktet. Figuren viser ein bil som kjører mot venstre og bremsar. Då virkar det friksjonskrefter mellom bakke og hjula - her vist som Bf og Br. Vi veit jo at tyngda G virkar gjennom tyngdepunktet, men problemet er at både Bf og Br vil prøva å dreia bilen mot klokka på figuren. Den einaste måten normalkreftene på hjula kan stoppa denne rotasjonen er ved at Lf er større enn Lr. Dette betyr at bakhjula mister veigrep. Hvis dette skjer i ein sving, vil bilen tendera til å overstyra slik at ein får skrens. Derfor er det lurt å bremsa før svingen!
Ved akselerasjon vil situasjonen vera motsatt av figuren over, dvs ein vil få større marktrykk på bakhjula. Hvis bilen har bakhjulsdrift treng ikkje dette vera ein ulempe, sidan ein då har mindre sjans for å spinna, men generelt er vektoverføring ein ulempe fordi auken i veigrep ein kan få på eit eller to hjul er mindre enn tapet på dei andre, slik at ein alt i alt mister veigrep.
I ein sving vil ein i tillegg bilen få større vekt på ytterdekka enn innerdekka. Dette får bilen til å krenga, og i verste fall rulla over, og bilen vil mista grepet på dei indre dekka.
Når der gjeld bilens konstruksjon kan ein forsøkja å 1) Gjera den lettare. Mindre vekt betyr mindre vekt å forskyva. 2) Senka tyngdepunktet dvs. i praksis å gjera bilen lavare, eller 3) Auka sporvidden. I racing prøver ein å laga så lave bilar som mulig, men bredden er som regel begrensa gjennom reglane.
Banked turn. (Dosert sving)
Remember When Banked Turns Ruled Racing?
https://www.circuitsofthepast.com/raceoptimal.com/ Database med optimale linjer på forskjellige banar som er generert av ein Genetisk Algoritme. Sjå også Physics.
The Ten Fastest Ovals Outside The US.
Korleis finna ut om bilen er på banen? Car simulation to demonstrate screen wrapping ... Testing for image collision Pygame ... brukar get_at(x,y) .. How to get a pixel color outside of screen in pygame?
Program a Racing Car. Tøft!
Reinforcement learning in Python to teach an RC car to drive itself — Part 3 ---
Self-driving (very small) cars — Part I.
How to build a self-driving robot race car.
Donkey Car !!!
PiCar-S Raspberry Pi 3/2/B+ Smart Car Kit.