8Q-problemet

Eit klassisk problem er det såkalte Eight Queens Puzzle. Det går ut på å plassera åtte dronninger på eit sjakkbrett uten at noken av dei angriper ei anna. Husk at dronninga kan angripa både vertikalt, horisontalt og diagonalt, så det er åpenbart ikkje mulig å plassera fleire enn åtte. Men det viser seg at åtte er mulig. Problemet har faktisk 12 ulike såkalt fundamentale løysingar når vi ikkje inkluderer symmetriske variantar, dvs. variantar som er like hvis vi speiler eller roterer dei. Ei av løysingane av ser slik ut:

Test deg sjøl her eller her, om du klarer å finna ei anna løysing!

Kor god er ei løysing?

Før vi går i gang med mulige løysingsmetodar, treng vi eit mål for kor godt eit løysingsforslag er. Det vanlige er antalet dronningpar det fins på brettet som angrip kvarandre. Vi kan kalla denne variabelen h. Eksempelvis gir stillingen på brettet under h = 17. Dette er med andre ord ei dårlig løysing fordi det er 17 dronningpar som angrip kvarandre. Finn du alle?  Målet vårt er sjølsagt h = 0. Så spørsmålet er: korleis kjem vi dit?

Brute Force

Ein metode som alltid virkar, så lenge det er eit endelig antal løysingar som kan vurderast innan rimelig tid, er rett og slett å testa alle mulige variantar. Denne metoden kallast ofte Brute Force. Problemet med den er at den tar fryktelig lang tid når det er mange variantar. Q8-problemet har 4,426,165,368 løysingar. Hvis ein generaliserer problemet til større sjakkbrett, så vil dette fort bli umulig å gjennomføra. 

Hillclimbing:

Nedanfor skal vi sjå på ein forenkla variant av Q8-problemet med fire dronninger, og prøva å løysa den manuelt med såkalt Hillclimbing. Ein liten kommentar til navnet: Vi vil ha antal feil ned, og dermed kan vi sei at vi klatrar høgare opp i "godhet", (eller det vi kan kalla fitness når vi snakkar om Genetiske Algoritmar, sjå nedanfor.) Vi er altså ute etter ein iterativ algoritme som gir oss lavare h-verdi for kvar iterasjon. Vi ser først på eit forenkla problem, nemlig eit 4x4-brett:

Vi startar med ein stilling der alle dei fire dronningene er plassert tilfeldig. Anta at vi er gitt oppstillingen på den første figuren over, som gir h = 5 gjensidige truslar (markert med linjer). Algoritmen vi vil prøva er kort og godt: "reduser h så mykje vi kan for kvart steg". Det første vi åpenbart må prøva, er å flytta ei av dei to dronningene med tre truslar mot seg, fordi tre er det største antalet truslar ei dronning har i denne stillinga. Og då ser vi at hvis vi flytter dronninga på b3 eit rute opp til b4, så fjerner vi alle dei tre truslane og står igjen med to, altså h = 2, som vist i figur tre. Dette er det beste åpningstrekket vi kan gjera fordi alle andre gir mindre eller likt. Det neste logiske steg er å prøva å flytta dronninga på c2 som har to truslar mot seg. Og vi ser at hvis vi flytter vi denne dronninga ned til c1, så fjernar vi begge disse. Då er vi nede på null truslar, og problemet er løyst!

Her var vi heldige og kom i mål. Hvis du prøver med andre startoppstillingar, så vil du sjå at vi ikkje kjem heilt i mål uten at vi gjer trekk som ikkje endrar h-verdien. Q8-problemet er sjølsagt endå  vanskeligare, så denne metoden vil ikkje alltid finna løysinga.

Back-tracking:

Ein betre metode er ein såkalt back-tracking-algoritme, og her kan du lesa ein god forklaring korleis vi kan løysa N-queens problemet med Google Optimization Tools, som også har ei side med Traveling Salesman-problemet. Prinsippet med back-tracking er at ein startar å plassera ut dronningene ei for ei. Det viktige er at for kvar ny dronning  du plasserer  ut, så må du passa på at den ikkje er i konflikt med dei forrige. Hvis du ikkje klarer det, så må du hoppa tilbake ett eller fleire steg. Og poenget er at du bare hopper så langt tilbake som du må. Så hvis du har prøvt ut alle mulige trekk i det forrige steget, så må du enda eit tilbake, osv. I eksempelet under plasserer vi ut ei og ei dronning, og for kvart steg viser vi kor mange plasser som blir trua med kryss. Dei raude kryssa er dei som er komt til frå forrige utplassering. Hvis ei rad eller kolonne er fyllt opp med kryss, så har vi ingen stad å plassera ei dronning, og vi må tilbake. Vi prøver igjen med 4x4-brettet:

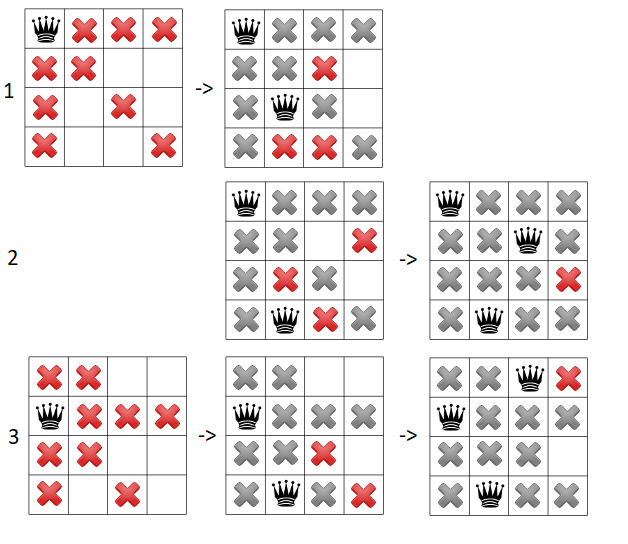
Forklaring: Vi plasserer ut dronninger linje (det sjakkspelarar kallar kolonnene) for linje.

1. I første forsøk plasserer vi ei dronning øverst i a-linja, dvs i a4. Den vil då blokkera rutene som er markert med raude kryss. Så prøver vi ei ny dronning i  b2, som blokkerer ytterligare tre ruter. Og dermed ser vi at alle rutene i c-linja er stengt, og vi må derfor tilbake til steg 2.
2. Vi har altså fremdeles dronning i a4, men prøver no å putta neste dronning på b1, som blokkerer tre nye ruter. Vi har no ein åpning i c3. Men vi ser at når vi plasserer ei dronning der, så sperrar vi alle rutene i d-linja. No må vi heilt tilbake til steg 1, fordi vi har prøvd alle muligheter med dronning i a4.
3. No går vi ei rute ned og set dronninga i a3 som blokkerer 9 ruter. Det er no bare ei rute ledig i b-linja, nemlig b1, og vi må setja dronninga der. Den blokkerer to nye ruter, men vi har åpning i c4. Med ei dronning i c4 blir d4 blokkert, men vi har no åpning i d2. Dermed kan vi setja den fjerde og siste dronninga der, og vi er ferdig!

Genetiske Algoritmer

Backtracking gir oss altså alltid svar. Spørsmålet er om den er effektiv nok? Eit paper frå 2014 og eit anna frå 2015 tyder på at ein Genetisk Algoritme kan vera meir effektiv. Genetiske Algoritmer optimaliserer ved å ha ein populasjon med mange "kromosomer", dvs. lister, som kvar for seg representerer eit forslag til løysing på problemet vårt. Så, korleis gjer vi dette på ein fornuftig måte for Q8-problemet? Ein måte, som har blitt brukt, er å bruka ei liste med åtte siffer, der kvart siffer representerer raden i den tilsvarande linja (dvs. kolonnen). For eksempel betyr lista [5,3,1,7,2,8,6,4] at dronninga i a-linja skal stå i rad 5, dronninga i b-linja skal stå i rad 3, osv. Det gir følgande stilling på brettet:

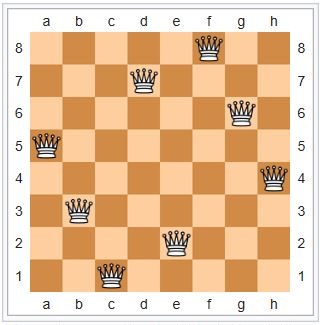
Sånn en passant (eg kunne ikkje dy meg) kan vi nevna at dette faktisk er den einaste symmetriske løysinga til Q8-problemet. Den er symmetrisk med hensyn til 180 graders rotasjon, og denne stillinga har derfor bare fire symmetriske variantar som er ulike, i motsetning til alle dei andre fundamentale variantane som har åtte. Og derfor får vi at det totale antalet løysingar (inkludert symmetriske variantar) er  11*8 + 1*4 = 92.

Fitness

I ein GA vil vi starta med mange kromosomer (lister) som vi genererer tilfeldig*. Så vil vi rekna ut fitness for kvar enkelt kromosom. Ein brukbar måte å gjera dette på er rett å slett å setta fitness = (28-h) der h er, som før, antalet dronningpar som angrip kvarandre. Ei løysing har, som vi veit, h = 0, så då bli fitness lik 28. Talet 28 er valgt fordi det er det maksimale antal angripande dronningpar på eit brett. Det får vi når alle dronningene står på ei linje. For å rekna ut dette, kan du tenkja at den første dronninga er i konflikt med sju andre. Den andre er i konflikt med den første (som vi alt har telt opp) og dei seks andre. Den tredje med dei to første (som vi også har talt opp) pluss dei fem andre, osv. Totalt får vi få 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28.

Krysning og mutasjon

Så vi har altså eit antal lister som vi har rekna ut fitness for. Det som skjer vidare er at vi lar dei med høgast fitness, dvs. dei som har dei beste løysingane, få lov til å få avkom. Det gjer vi ved å kryssa to kromosom, som då gir to nye - eller mutera eit enkelt kromosom for å få eit nytt. Dette kan vi gjera på ein gong, slik figuren under viser:

Forklaring: Vi starter med dei to listene [3, 2, 7, 5, 2, 4, 1, 1] og [2, 4, 7, 4, 8, 5, 5, 2]. Dette er "foreldrene". Så krysser vi dei. Det kan vi gjera* ved å kutta dei (for eksempel) etter det tredje "genet", og bytta resten av listene som kjem etter. Det resulterer i listene [3, 2, 7, 4, 8, 5, 5, 2] og [2, 4, 7, 5, 2, 4, 1, 1]. Dette er "barna". Til slutt muterer vi (tilfeldigvis) det øverste kromosomet på plass nr. 6. Verdien 5 blir til to, og vi får [3, 2, 7, 4, 8, 1, 5, 2].

Nedanfor viser vi korleis dette ser ut når vi tegnar posisjonane på brettet til begge foreldrene, samt det øverste av barna (i gult) før og etter mutasjonen:

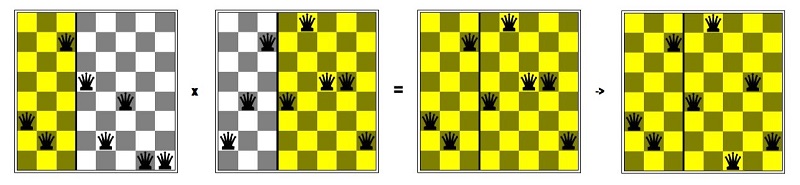
Når vi har produsert avkom for eit antal av dei beste foreldrene, så sit vi igjen med ein ny populasjon, som vi så må berekna fitness for. Denne populasjonen  inneheld kanskje kromosom som er betre, og diss vil vi då fortsetja å "avla" på. Deretter fortset algoritmen heilt til vi har funne ei optimal løysing eller til max antal iterasjonar er oppnådd.

* Litt meir om kromosomene våre. Slik vi har laga kromosomar våre, så vil vi aldri kunna få fleire enn ei dronning per linje. Dermed unngår vi mange oppstillingar som umulig kan vera rette. Hvis vi i tillegg lar alle startkromosoma våre, vera permutasjonar av [1, 2, 3, 4, 5, 6, 7, 8], så vil dette garantera at vi i første generasjon heller ikkje har konflikter i horisontal retning. Vi vil med andre ord bare ha konflikter på skrå  første generasjon. Kan vi sørga for at dette held også for dei neste generasjonane? Ja, men i såfall må vi laga litt meir "intelligente" krysnings- og mutasjonsreglar, som sørger for at avkomma aldri har tal som gjentar seg i lista. (Prøv!) Då vil heller ikkje avkomma ha konflikter i horisontal eller vertikal retning. Det vil gi eit meir effektiv søk, og det vil gi ein enklare måte å sjekka antal konflikter på.

Også andre algoritmar kan brukast til dette problemet, men det tar vi ikkje opp her.

LENKER

Backtracking | Set 3 (N Queen Problem).

Simulated Annealing for beginners.

n-queens problem using Pyevolve. Pevolve er

Simulated Annealing. Q8-eksempel med kode (C)

N-Queens Part 2: More Algorithms frå letstalkdata. Bruker sim ann.

Comparison of Heuristic Algorithms for the N-Queen Problem.

Applying a genetic algorithm to the traveling salesman problem.

Python har egen pakke for dette!

Verdensrekordar for NQ-problemet.