Primtall

Her skal vi sjå på tre relaterte problem, nemlig

Korleis kan vi sjekka om eit gitt tall er eit primtall?
Korleis kan vi skriva eit gitt tall som eit produkt av primtal?
Korleis kan vi generera ei liste med alle primtal opp til N?

Til kvar av disse problemstillingane lagar vi eit løysingsforslag. Disse er på ingen måte optimale program. Dei kan lagast både meir effektive og meir elegante. Men dei er forhåpentlig forståelige.

Eit primtall er eit tall som ikkje kan delast på andre tal enn 1 og seg sjøl. Og med dette meiner vi at når vi dividerer, så skal vi ikkje få ein rest. Python-måten å gjera dette på, er å bruka operatoren % som gir oss resten. Hvis vi skriv 7%3, så får vi 1 som svar. Det fortel oss at talet 7/3 kan skrivast som 2 1/3. For oss er heile poenget at divisjonen ikkje gir eit heiltallig svar. Når vi dividerer 6/3, så veit vi at vi får 2, og ingen rest. Med python ser vi at 6%3 gir 0. Altså kan vi sjekka om t : n gir eit heiltall ved å bruka testen if t%n == 0:

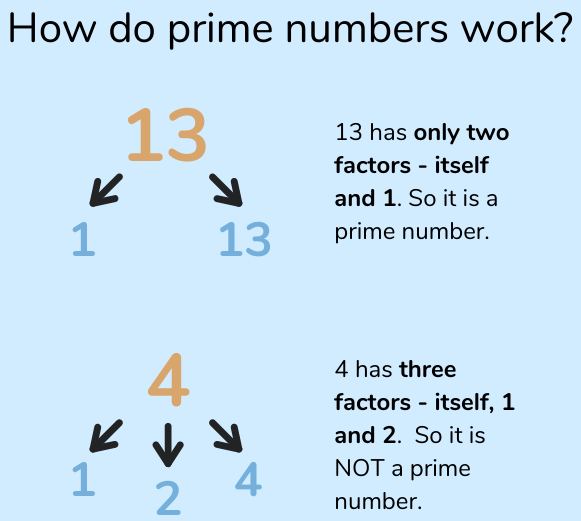
1 Sjekk for primtall

Ein litt "naiv" algoritme vil då vera å bruka restoperatoren på alle tal opp til talet. Hvis vi for eksempel skal sjekka om 9 er eit primtal, så må vi i såfall sjekka 9%2, 9%3 osv. opp til 9%8. Vi treng jo ikkje å sjekka hverken 9%1 eller 9%9. Men vi ser også fort at sidan 9%3 = 0, dvs. at 9 kan delast med 3, så treng vi ikkje sjekka dei andre. Vi avsluttar altså søket straks vi har funne ein faktor (3 i dette tilfellet) for då har vi funne ut at 9 ikkje er eit primtal.
Så ein litt mindre opplagt oppdagelse: vi kan faktisk stoppa søket ved kvadratrota av talet. Tankegangen er som følger: hvis eit tal har ein faktor som er større enn kvadratrota av talet, så har den også ein annan faktor som er mindre, og denne har vi i såfall alt funne. For eksempel har talet 35 faktorane 5 og 7. Kvadratrota av 35 er 5.9 (avrunda), så den ein faktoren (5) er mindre og den andre (7) større. Slik vil det alltid vera. Hvis vi hadde hatt to faktorar større enn 5.9, så ville produktet av dei vera større enn 35.

Programmet:

Som du ser har vi lagt inn ei while-løkke først, for å ha ein veldig enkel sjekk at talet vi gir inn er større enn ein. Egentlig burde vi også sjekka om det faktisk er eit tal. No treng vi ei løkke frå 2 til og med kvadratrota av "tall". Derfor vi gjer om kvadratrota av tall til eit heiltal, men sidan range stoppar ein før grenseverdien, så må vi leggja til ein. Hvis for eksempel tall = 49, så skal vi sjekka alle tal frå og med 2 til og med 7. Det oppnår vi ved å bruka range(2,8)


import math

tall = 0 # Vi treng ein startverdi for tall, men den blir endra etterpå.

# primtal er større enn 1
while tall <=1:
    tall = int(input("Skriv inn eit heiltal større enn 1: "))
else:
   # sjekk for faktorar
   for sjekk in range(2,int(math.sqrt(tall))+1):
       if (tall % sjekk) == 0:
           print(tall,"er ikkje eit primtal")
           break
   else:
       print(tall,"er eit primtal")

Kjøring:

Merk at programmet vil krasja hvis du feks. skriv inn "ost"! Men for alle heiltal skal det funka.


Skriv inn eit tal større enn 1: 84
84 er ikkje eit primtal

Skriv inn eit tal større enn 1: 29
29 er eit primtal

2 Primtalfaktorisering

Her er oppgåva å finna alle primtalsfaktorane i eit gitt tal. Hvis vi skriv inn 84, så skal programmet skriva ut at 84 = 2 * 2 * 3 * 7. Så vi finn først resten etter divisjonen 84 / 2, og får 0. Då har vi funne ut at 84 er delelig med 2, og vi kan utføra heiltallsdivisjonen 84//2 som gir 42. Dermed veit vi at 84 kan faktoriserast som 84 = 2 * 42. Men vi må fortsetja med 42 fordi dette ikkje er eit primtal. Derfor set vi tall = 42 og fortset å dividera med 2 så lenge "tall" er delelig med 2. Vi finn at 42 = 2 * 21. Men 21 er ikkje delelig med 2, så vi aukar sjekk med 1 og prøver 21%3. Det funkar. Så no blir tall lik 7. Dette er eit primtal, og derfor stoppar algoritmen.

Programmet:

Vi tar vare på alle faktorane vi har funne, dvs. kvar gong tall%sjekk er lik null, tar vi vare på talet "sjekk". Men den siste faktoren er talet "tall" sjøl. Så til slutt tar vi med den også.


start = int(input("Skriv inn tal som skal faktoriserast: "))
tall = start
svar = ""    # svar er ein tekststreng som vi puttar faktorane inn i etterkvart som vi finn dei.
sjekk = 2    # Første mulige faktor som vi sjekkar er 2

while sjekk**2 <= tall:                 # Så lenge kvadratet av sjekk er mindre eller lik tall       
    if tall % sjekk == 0:               # Hvis tall er delelig med sjekk...
        svar += str(sjekk)   		    # ...så er sjekk ein faktor som vi tar vare på
        tall = tall//sjekk              # Vi dividerer med sjekk og fortset å jobba med kvotienten
        if tall != 1:                   # Hvis tall er 1 er vi ferdige, hvis ikkje...
            svar += "*"                 #  ... legg vi til eit gangetegn
    else:                               # ellers (tall er ikkje delelig med sjekk)...
        sjekk += 1                      # Hvis tall ikkje er delelig med sjekk prøver vi neste
 
if tall != 1:                           # Det som no er igjen av tall er den siste faktoren
    svar += str(tall)        		    # og den må vi også ta vare på.

print (start, "=",svar)

Kjøring:


Skriv inn tal som skal faktoriserast: 6731216640
6731216640 = 2*2*2*2*2*2*2*2*3*3*3*3*3*5*17*19*67

3 Eratosthenes sil

Dette er ein gammal algoritme etter grekaren Ἐρατοσθένης. Metoden er best å forklara med ein figur:

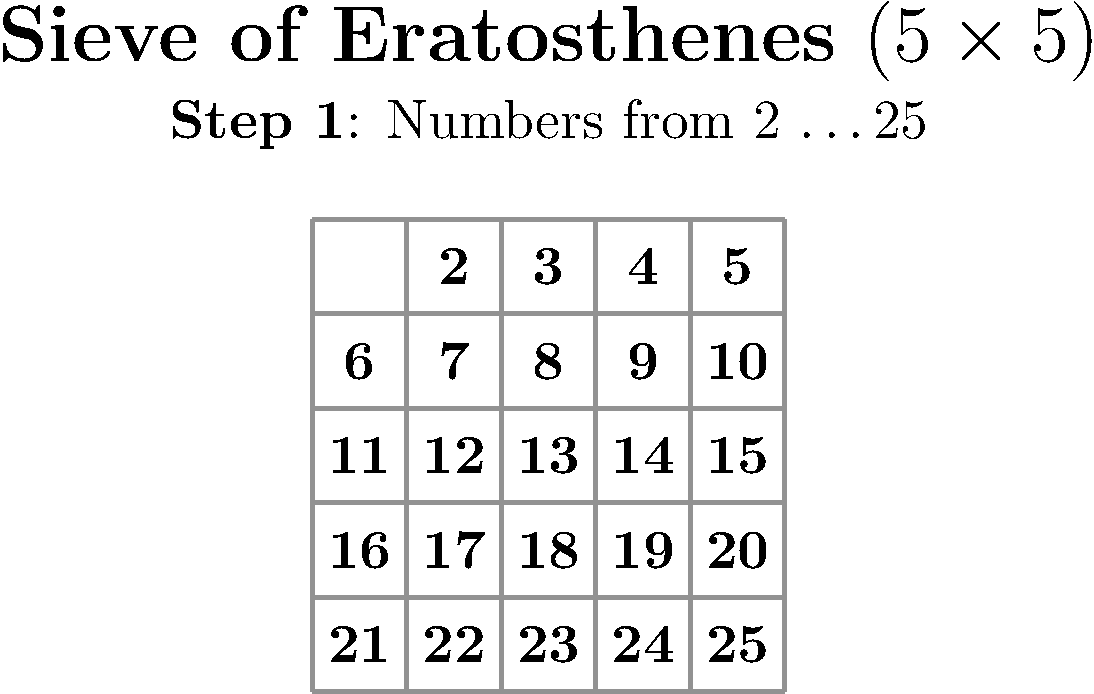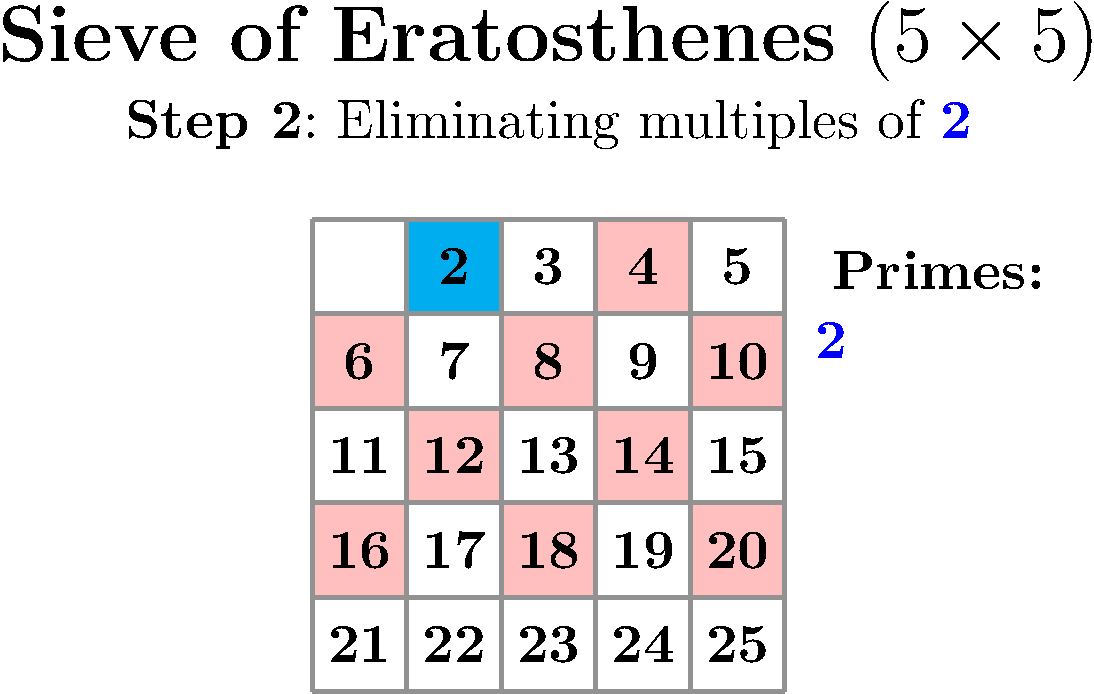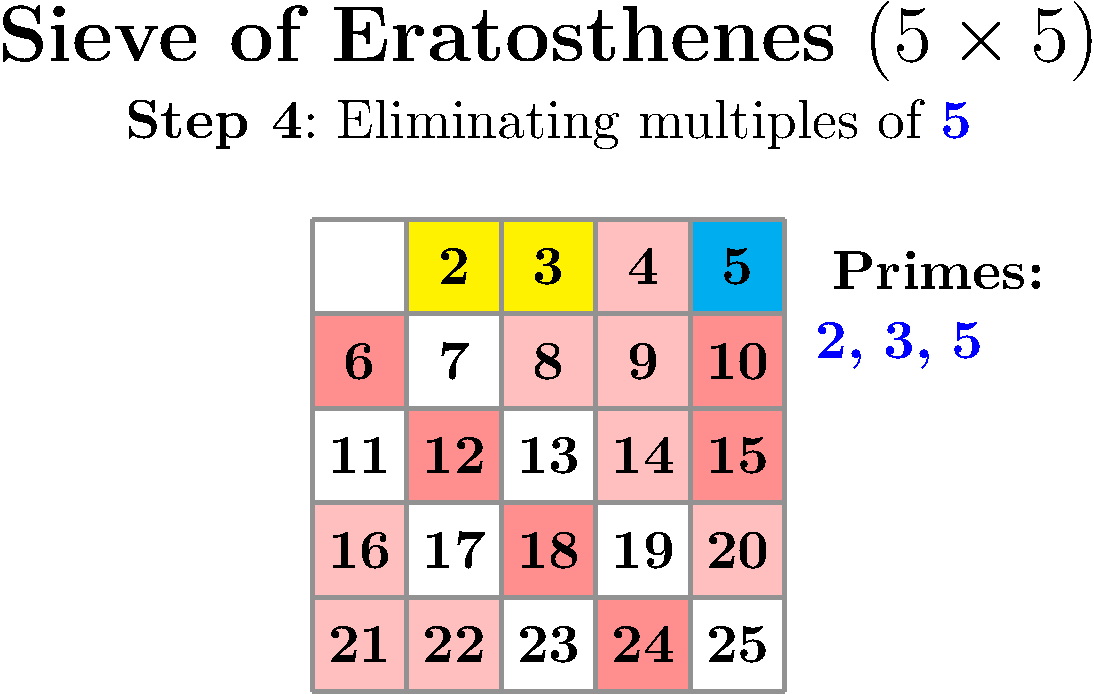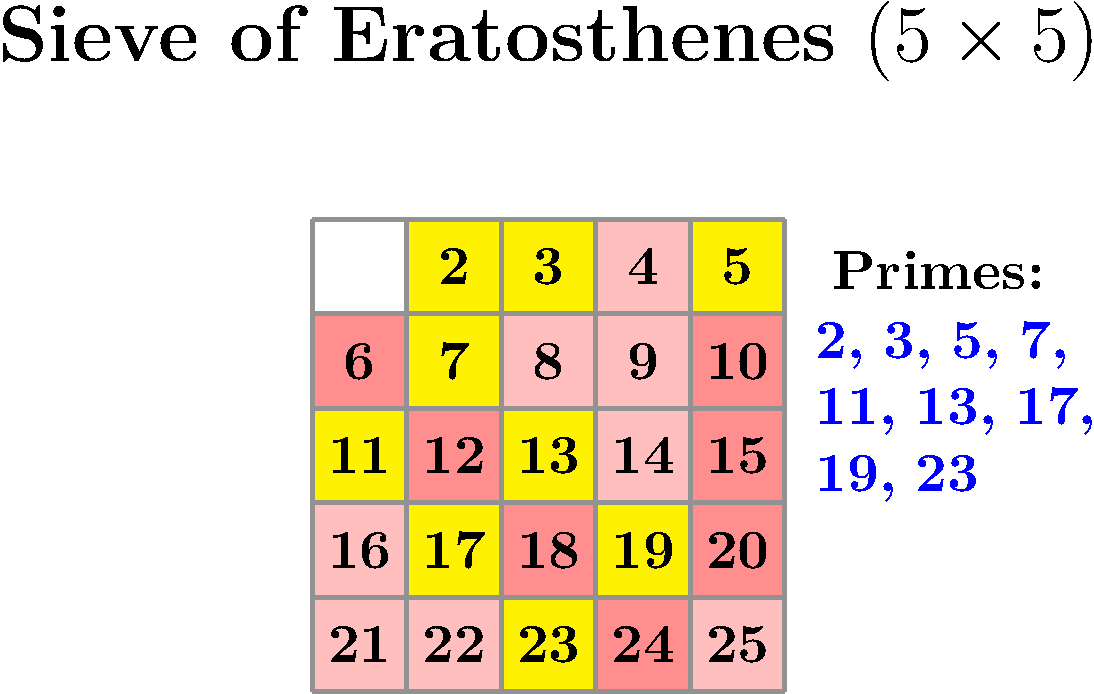
Tankegangen er at vi først lagar ei liste over alle potensielle primtal frå og med 2, og til og med N. Så startar vi med det første primtalet, dvs. 2 og "krysser vi ut" alle multippel av 2 (4,6,8 osv.). Deretter finn vi det neste primtalet på lista, som er 3, og krysser ut alle multippel av 3 (6,9,12) osv. Med denne prosessen kjem vi til å kryssa ut ein del tal som allerede er kryssa ut, men det funkar jo likevel. Når vi er ferdige, så er det bare primtal igjen.

Programmet:

Vi lar N vera 25 og lagar ei liste med Boolske variablar (False eller True). Hvis primtall[5] er True, så betyr det at primtallet med indeks 5 faktisk er eit primtal. Men til å begynna med lar vi alle vera True, bortsett frå dei to første i lista. Husk at disse representerer tala 0 og 1. Ingen av disse er primtal, så vi set primtall[0] = False og primtall[1] = False. Dette er kanskje litt overpedantisk, sidan disse to aldri blir brukt i programmet. Men rett skal vera rett :)

Utkryssinga består av å setja alle multippel av eit tal p, feks 2, til False. Det gjer vi med ei for-løkke der indeksen skal løpa frå n² til (men ikkje inkludert) N+1, i steg på n. Etter at vi har kryssa ut alle multippel av p, aukar vi p med ein. Hvis p ikkje er kryssa ut, vil dette vera eit primtal, og vi kan fortsetja å kryssa ut multippel av dette.


N = 25 

primtall = 2*[False] + (N-1)*[True]

p = 2
while (p * p <= N):
 
    if (primtall[p] == True):
 
        # Krysser ut alle multippel av p:
        for i in range(p * p, N+1, p):
            primtall[i] = False
    p += 1
 
# Utskrift av alle primtal
for p in range(2, N+1):
    if primtall[p]:
        print(p,end=" ")

Kjøring:

Med N = 25 får vi ut dette:


2 3 5 7 11 13 17 19 23