Det bestemte integralet med trapesmetoden

Før du les denne leksjonen bør du ha lest om rektangelmetoden, og kanskje også litt om numerisk integrasjon. Vi skal finna ein tilnærma verdi for det bestemte integralet mellom 1 og 7 av funksjonen

$f(x) = x³ - 9x² + 23x - 5$.

Denne gong skal vi gjera det ved hjelp av trapesmetoden. Sidan f(x) > 0 i heile dette området, er det det same som å finna arealet som er markert under. Fasiten er 96.

title

Vi deler opp i N = 12 trapes:

title

Vi skal først finna arealet av trapeset som er markert med grønt, så vi startar med å definerer f, og finna høydene på begge sider:

In [1]:
def f(x):
    return x**3 - 9*x**2 + 23*x - 5

La oss testa:

In [2]:
print("f(3)=",f(3))
print("f(3.5)=",f(3.5))

f(3)= 10
f(3.5)= 8.125

På same måten som med rektangelmetoden, legg vi inn nedre grense a (=1) og øvre grense b (=7) for arealet, samt antalet rektangel N (=12), Dermed kan vi rekna ut bredden av trapea, som vi kallar dx:

In [3]:
a = 1 # nedre grense
b = 7 # øvre grenseN = 3 
N = 12 # antal trapes
dx = (b-a)/N #Bredden av trapesa

print("dx =",dx)

dx = 0.5

Det vi no treng å gjera er å laga ei løkke som reknar ut arealet til kvar av rektangela, og summerer disse. Som vi veit er formelen for arealet av eit trapes med sider a og b, og høyde h: $A = \frac{a+b}{2}\cdot h$. Slik ser det vanligvis ut:

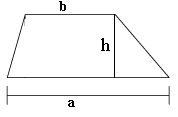
trapes

Men vi må snu figuren på høgkant og gi nye navn til sidene. Vi kallar x-verdien i venstre side for xv og for høgre side xv. Lengdene a og b blir då til funksjonsverdiane (dvs. y-verdiane) f(xv) og f(xh). Og høyden h blir avstanden mellom xv og xh, nemlig dx: 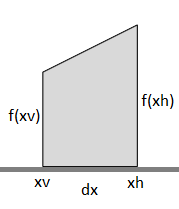trapes Dermed blir formelen vår sjåande slik ut:

A = dx*(f(xv)+f(xh))/2

Vår jobb er no å rekna ut xv og xh. "Vårt" trapes har xv = a + 4*dx, dvs. 3, og xh = xv + 0.5, dvs 3.5. Arealet blir dermed:

In [4]:
n = 4 #Vi testar om det virkar for det aktuelle trapeset. Husk at vi startar å telja med 0!
xv = a + n*dx
xh = xv + dx
A = dx*(f(xv)+f(xh))/2
print("Arealet av det femte trapeset er:",A)

Arealet av det femte trapeset er: 4.53125

Når vi legg dette inn i ei løkke blir det slik:

In [5]:
S = 0
for n in range(N):
    xv = a + n*dx
    xh = xv + dx
    A = dx*(f(xv)+f(xh))/2
    S += A

print("Summen av",N,"trapes er:",S)

Summen av 12 trapes er: 96.75

Vi er allerede ganske nær fasit. No lagar vi ein funksjon trapesmetoden, og legg inn kode for å tegna funksjonen. Programmet vårt ser no slik ut:

In [8]:
import matplotlib.pyplot as plt
import numpy as np

def trapesmetoden(f,a,b,N):

    plt.xlabel('x')
    plt.ylabel('y')
    plt.title("Trapesmetoden:")
    plt.plot([a,b],[0,0],color='blue') # Horisontal linje frå a til b

    dx = (b-a)/N #Bredden av trapesa
    S = 0
    for n in range(N):
        xv = a + n*dx
        xh = xv + dx
        A = dx*(f(xv)+f(xh))/2
        S += A
    
        plt.plot([xv,xv],[0,f(xv)],color='blue') # Vertikal linje i xv
        plt.plot([xh,xh],[0,f(xh)],color='blue') # Vertikal linje i xh
        plt.plot([xv,xh],[f(xv),f(xh)],color='blue') # Skrå linje frå (xv,f(xv) til (xh,f(xh)))

    print("Summen av",N,"trapes mellom a =",a,"og b =",b,"er:",S)

    x = np.linspace(a,b,100) # Genererer 100 x-verdiar mellom a og b       
    plt.plot(x,f(x),color='red') # Plotter sjølve funksjonen
    
    plt.show()

trapesmetoden(f,1,7,12)

Summen av 12 trapes mellom a = 1 og b = 7 er: 96.75

La oss testa med litt større N:

In [7]:
trapesmetoden(f,1,7,100)

Summen av 100 trapes mellom a = 1 og b = 7 er: 96.01079999999996

Oppgaver

  1. Test ut programmet for ulike verdiar av a, b og N
  2. Prøv programmet for andre funksjonar
  3. Samanlikn kjøringane med rektangelmetoden. Kva ser du? Korfor trur du det blir slik?
In [ ]: