Båtar i horisonten: Vi kjenner alle til at båtar som reiser frå oss, til slutt forsvinn bak horisonten. Men kor langt er det egentlig til horisonten, dvs., kor langt er det til det punktet der båten begynner å forsvinna?

Matematikken bak:

Dette er bare ein omtrentlig utrekning, sidan vi antar at jorda er ei perfekt kule, med radius r = 6378137 meter. Vi antar også at horisonten er i havnivå, dvs. at det ikkje er noken fjell eller høyder.
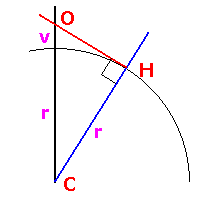
Utrekning: Vi tegnar ein rettvinkla trekant CHO, der C er sentrum av jorda, H er punktet i horisonten H, og O er punktet vi observerer frå. Når vi kjenner høyden over havet som vi observerer frå (v på tegningen) så kan vi rekna ut avstanden OH ved hjelp av Pytagoras sin setning. Hypotenusen i trekanten CO = v + r. Den eine kateten er r og den andre er OH, som vi skal finna. .

Eksempel: Hvis vi står på dekk ombord i ei seilskute, så kan det henda at observasjonshøyden vår er 5 m. Då vil horisonten vera 8 km unna. Men hvis vi klatrar opp i toppen av masta, vil vi kanskje observera frå ei høgde på 20 m. Då vil horisonten vera 16 km unna. Vi ser altså dobbelt så langt.
Det motsette er også tilfelle. Frå havnivå (punkt H) vil vi i klart ver, vera i stand til å sjå toppen(O) av eit 1000m høgt fjell som er 112.9 km unna.